Системи лінійних диференціальних рівнянь із сталими коефіцієнтами

Приклад 8.1.

Розв’язати систему рівнянь

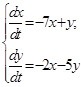
● Продиференціюємо перше рівняння:

.

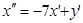Підставимо в це рівняння значення похідної 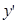із другого рівняння системи

.

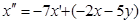Знайшовши з першого рівняння значення 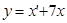і підставивши його в знайдене рівняння, дістанемо

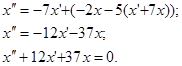
Маємо лінійне однорідне рівняння другого порядку із сталими коефіцієнтами. Інтегруючи його, одержуємо: 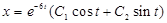. Оскільки 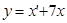, то

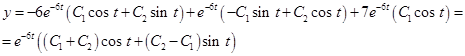
Отже, загальний розв'язок даної системи має вигляд:

●

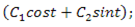
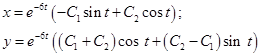
Нехай задана нормальна система лінійних диференціальних рівнянь із сталими коефіцієнтами. Для зручності обмежемося трьома рівняннями:

(7)

де 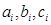- сталі. Цю систему, методом виключення змінних, завжди можна звести до одного лінійного однорідного рівняння третього порядку із сталими коефіцієнтами. Розглянемо ще один метод розвязування системи (7).

Шукатимемо окремі розвязки системи у вигляді

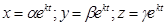, (8)

де α,β,γ – невизначені сталі, які треба знайти.

Підставивши функції (8) в систему (7) і скоротивши на множник 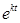≠0, дістанемо:

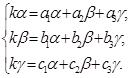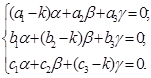або (9)

Дістали алгебраїчну однорідну систему лінійних рівнянь. Щоб ця система мала ненульові розвязки, необхідно і достатньо, щоб визначник системи дорівнював нулю:

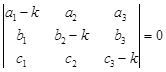(10)

Розкривши визначник, дістанемо алгебраїчне рівняння третього степеня відносно 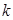, яке називається характеристичним рівнянням системи (7).

Розглянемо випадок, коли рівняння (10) має три дійсні різні корені 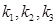. Для кожного з цих коренів запишемо систему (9) і визначимо невідомі 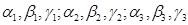. Можна довести, що загальний розвязок системи (7) має вигляд:

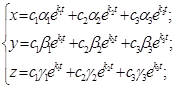(11)

Випадки, коли рівняння (10) має кратні або комплексні корені, складніші, і ми їх не розглядатимемо. У звязку з цим зауважимо, що характеристичне рівняння (10) системи (7) збігіється з характеристичним рівнянням диференціального рівняння третього порядку, до якого зводиться система (7). Таким чином, якщо відомі корені рівняння (10), то завжди можна знайти загальний розв'язок рівняння третього порядку, до якого зводиться система (7), а потім і загальний розвязок самої системи (7).

Отже, незалежно від структури коренів характеристичного рівняння, систему (7) завжди можна розвязати, якщо тільки відомі ці корені.

Дата добавления: 2014-12-17