Векторы и простейшие действия над ними

ТЕМА 7. ВЕКТОРНАЯ АЛГЕБРА

Свободный вектор а (т.е. такой вектор, который без изменения длины и направления может быть перенесен в любую точку пространства), заданный в координатном пространстве Oxyz, может быть представлен в виде

a =a_xi+a_yj+a_zk.

Такое представление вектора а называется его разложением по осям координат, или разложением по ортам.

Здесь ах, ау, az—проекции вектора а на соответствующие оси координат (их называют координатами вектора a, i, j, k—орты этих осей (единичные век­торы, направление каждого из которых совпадает с положительным направлением соответствующей оси).

Векторы a_xi, a_yj, a_zk, в виде суммы которых представлен вектор а, назы­ваются составляющими (компонентами) вектора а по осям координат.

Длина (модуль) вектора а обозначается 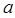или | а | и определяется по формуле

.

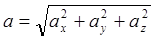Направление вектора а определяется углам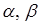и и 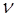образованными им с осями координат Ох, Оу и Оz. Косинусы этих углов (так называемые направляющие косинусы вектора) определяются по формулам:

; ; .

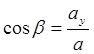Направляющие косинусы вектора связаны соотношением

.

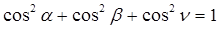Если векторы а и b заданы их разложениями по ортам, то их сумма и раз­ность определяются по формулам

a + b =(a_x+b_x)i+(a_y+b_y)j+(a_z+b_z)k,

a - b =(a_x-b_x)i+(a_y-b_y)j+(a_z-b_z)k.

Напомним, что сумма векторов а и b, начала которых совмещены, изобра­жается вектором с тем же началом, совпадающим с диагональю параллелограмма, сторонами которого являются векторы а и b. Разность a - b этих векторов изображается вектором, совпадающим со второй диагональю того же параллелограм­ма, причем начало этого вектора находится в конце вектора b, а конец — в конце вектора а (рис. 7.1).

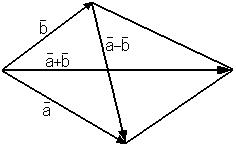
Рис. 7.1

Произведение вектора а на скалярный множитель m определяется формулой

m a =ma_xi+ma_yj+ma_zk.

Напомним, что векторы а и mа параллельны (коллинеарны) и направлены в одну и ту же сторону, если m > 0, и в противоположные стороны, если m < 0.

В частности, если m=1/a, то вектор а /а имеет длину, равную единице, и на­правление, совпадающее с направлением вектора а. Этот вектор называют единич­ным вектором (ортом) вектора а и обозначают а₀. Нахождение единичного вектора того же направления, что и данный вектор а, называется нормированием вектора а.

Таким образом, а ₀= а /а, или а = a а ₀.

Вектор , начало которого находится в начале координат, а конец — в точ­ке М (х; у; z), называют радиусом-вектором точки М и обозначают r (М) или просто r. Так как его координаты совпадают с координатами точки М, то его разложение по ортам имеет вид

r =xi+yj+zk.

Вектор 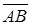, имеющий начало в точке A (x₁, y₁, z₁) и конец в точке В (x₂, y₂, z₂), может быть записан в виде 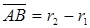, где r₂. — радиус-вектор точки В, а r₁ —радиус-вектор точки А. Поэтому разложение вектора АВ по ортам имеет вид

.

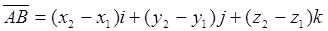Его длина совпадает с расстоянием между точками А и В:

.

Дата добавления: 2014-12-17