Замечание

Вычисление определенного интеграла. Формула Ньютона - Лейбница

Следствие.

Основные свойства определенного интеграла

1. 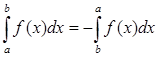(если поменять местами пределы интегрирования, то интеграл меняет знак).

2. Пусть интеграл 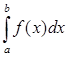существует и (т.е. а < с < b). Тогда

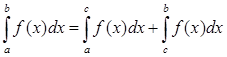
3. Пусть g - константа. Тогда

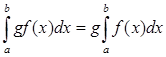(т.е. постоянный множитель можно выносить за знак интеграла).

4. 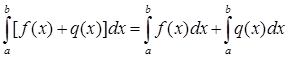(т.е. интеграл от суммы равен сумме интегралов).

Пусть 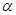и 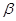- константы. Тогда

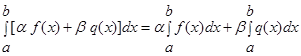
Это соотношение справедливо для любого конечного числа слагаемых.

Пусть функция f (x) непрерывна на отрезке [а, b]. Если функция F(x) является первообразной функции f (x) на 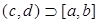(т.е. F'(x) = f (x) для всех 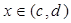, тогда

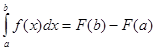(6.1)

(напомним, что на отрезке [а, b] переменная x принимает значения a<x<b в интервале (c,d):c<x<d. Формула (6.1) называется формулой Ньютона-Лейбница. Она является основной формулой интегрального исчисления.

Запись 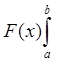называется двойной подстановкой и является краткой символической записью разности F(b)-F(a).

Дата добавления: 2014-12-17