Информационный подход к решению детьми логических задач

Информационный подход и теория Пиаже

Наиболее уязвимым местом в теории Ж. Пиаже является понятие горизон-
тального и вертикального декаляжа, т.е. повторения на новом уровне фе-
номенов, которые были преодолены на предшествующей стадии развития.
Например, дети способны решать задачи на сохранение длины, но не мо-
гут справиться с задачами на сохранение объема. Объяснения Пиаже со-
стояли в том, что сохранение объема требует большей степени абстракции
и, следовательно, группировки операций, чем сохранение длины.

Информационный подход, с характерным для него анализом поэтапной
обработки информации и специфического участия в ней процессов вни-
мания, восприятия, памяти, мышления, позволяет по-иному проанализи-
ровать особенности решений задач, рассматриваемых Пиаже.

Исследователи попытались выделить те требования, которые ставятся
данными задачами перед детским вниманием, памятью и процессами при-
нятия решений. Такой детальный анализ привел к более точным предска-
заниям возможностей ребенка и более комплексному пониманию неудач.
Так, при решении задачи на сохранение длины ребенок должен сравнить
только два отрезка по одному измерению, тогда как для задачи на сохра-
нение объема необходимо рассмотреть два измерения — высоту и ширину
контейнера (см. рис. 13.1). Это увеличивает нагрузку на систему обработ-
ки информации и требует от ребенка более длительных усилий, которые и
объясняют более позднее появление данной способности.

Одной из задач Пиаже на оценку возможностей ребенка в достижении ста-
дии формальных операций в мышлении служила задача на уравнивание
весов, в которой ребенок должен был интегрировать два условия: число
грузиков и расстояние, на котором они находятся относительно точки опо-
ры (рис. 13.10).

Информационный подход и теория Пиаже

Тип задачи		Применяемое правило
	I	II	III	IV
1. Задача на равновесие. Одно и то же число грузиков с каж- дой 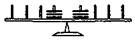стороны от точки опоры.
2. Задача на изменение веса. Существует неравное число грузиков на равном расстоя- нии от точки опоры с каждой стороны.
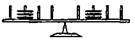
3. Задача на изменение рас- стояния отточки опоры. Су- ществует равное число грузи- ков с каждой стороны, но на разных расстояниях от точки опоры.		0 должен сказать «баланс»
4. Конфликт веса. На одной стороне больший вес, на дру- гой стороне больше расстоя- ние отточки опоры. Сторона с большим весом опустилась вниз.			шанс соответствия
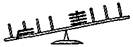
5. Конфликт расстояний. То же, что в предыдущей задаче, но сторона с весом на боль- шем расстоянии отточки опо- ры опускается вниз.		должен сказать «вниз правильно»	шанс соответствия
6. Конфликт равенства. Как при условиях 4 и 5, но две стороны в равновесии.		должен сказать «вниз правильно»	шанс соответствия

Рис. 13.10. Схема экспериментов Сиглера с балансиром, где дети должны учитывать соотно-
шение двух параметров для достижения равновесия: веса и длины плеча [Siegler, 1995].

1лава 13. Когнитивное развитие

Смглер [Siegler, 1991] провел анализ стратегий, которые используют дети
при решении задачи и выделил четыре правила (I, II, III, IV). Эти правила
отражают четыре уровня, на которых формируются стратегии.

Уровень 1: Правило I. Сторона с большей массой — тяжелее.

Уровень 2: Правило II. Используй правило I, но если грузиков одина-
ковое число, сторона, на которой грузики расположены дальше от точки
опоры, — тяжелее.

Уровень 3: Правило III. Масса и расстояние имеют значение вместе.
Когда существует конфликт, при котором одна сторона имеет большую
массу, а на другой стороне грузики расположены дальше от точки опоры,
тогда возникает путаница, и ребенок начинает гадать о решении.

Уровень 4: Правило IV. Масса и расстояние комбинируются для пра-
вильного решения, где учитываются масса и длина рычага для определе-
ния момента приложения силы (что соответствует характеристике фор-
мальных операций Пиаже).

Сиглер сконструировал 6 типов задач, которые могут выделить дети на
разных уровнях решения (см. рис.10). Так, в ситуации конфликта рассто-
яний от точки опоры дети на уровне 1 и 2 будут отвечать неверно, дети
уровня 3 будут отвечать иногда верно (уровень возможного), а дети уров-
ня 4 будут всегда отвечать верно.

Сиглер обнаружил возрастные различия в использовании разных пра-
вил. Трехлетние дети не могут использовать правила. Около 50% детей 4-х
лет используют правило I. Все пятилетние дети используют правило I. Де-
вятилетние дети одинаково распределяются в использовании правил II и
III. 13-ти и 17-тилетние почти всегда используют правило III. Даже среди
студентов колледжа только немногие могут использовать комплексную
причинность, заключенную в правиле IV.

Сиглер считает, что младшие дети испытывают трудности в решение за-
дач нахождения равновесия в связи с затруднениями совместить инфор-
мацию о массе и расстоянии одновременно. Во-первых, маленькие дети ог-
раничены в процессах запоминания. Во-вторых, они не имеют достаточ-
ных знаний, и им необходимы дополнительная информация и регуляция
для решения задачи.

Сиглер с коллегами использовали ситуацию, когда ребенок имел дело с
реальной шкалой равновесия, которая оставалась всегда на виду, и, сле-
довательно, ему не надо было запоминать ее. Дети могли проверять веса,
уточнять и повторять задачу. Дети пятилетнего возраста могли в таких ус-
ловиях решать задачу эффективно. Но, если оставался только один вид по-
мощи — или для запоминания, или в усвоении инструкции, трудности в
решении задачи возникали снова. Возможно, что ограничения в запоми-
нании и в использовании информации играли решающую роль в способ-
ности решения задач маленькими детьми.

Неопиажеанство

Дата добавления: 2014-11-29