Примеры. Пример 1. В ящике 7 белых и 9 черных шаров

Пример 1. В ящике 7 белых и 9 черных шаров. Наугад вынимают 1 шар. Найти вероятность того, что будут вынуты шары черного цвета

Решение: Пусть A - событие, состоящее в том, что вынутый черный шар.

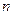=7+9=15 – число всех равновозможных исходов опыта.

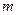=9 – число исходов благоприятствующих событию .

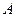Воспользуемся формулой классической вероятности: ;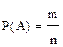

.

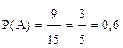Пример 2. Какова вероятность того, что при бросании игрального кубика выпадет больше четырех очков?

Решение. При одном броске может выпасть 1, 2, 3, 4, 5 или 6 очков. Благоприятные, то есть влекущие появление рассматриваемого события, исходы 5 и 6. Поэтому n = 6, m = 2, p = 2/6 = 1/3.

Пример 3. Какова вероятность того, что взяв две карты из колоды, получим два туза?

Решение. Будем считать, что в колоде 32 карты. Взять две из них можно 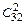способами. Двух тузов можно взять 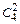способами. Поэтому .

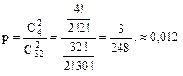Пример 4. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность того, что оба шара – белые?

Решение. Из 10 шаров вынули два шара, следовательно число всех случаев будет равно числу сочетаний из 10 элементов по два, то есть: 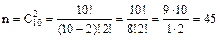. Число же случаев, благоприятствующих данному событию, определяется равенством

.

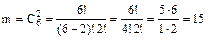Итак, .

Пример 5. В ящике 15 деталей, среди которых 10 нестандартных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что среди извлеченных деталей две будут нестандартные.

Решение: Пусть Событие А – среди извлеченных 4 деталей 2 нестандартные.

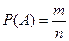
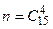– общее число четверок, которые можно сформировать из 15 деталей

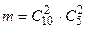– число четверок, благоприятствующих событию А.

По формуле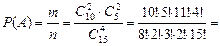

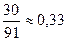
Пример 6: Какова вероятность угадать пароль из четырех цифр, если известно только, что все цифры пароля различны?

Решение. Событие А – пароль отгадан.

Количество благоприятствующих исходов m=1 (есть только один правильный набор цифр).

Общее число равновозможных исходов n= 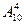(так как для составления определенной комбинации цифр порядок выбора значение имеет, то по формуле размещений выбираем 4 цифры из 10)

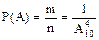, где

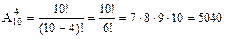
Значит,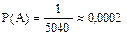

Пример 7. Шифр сейфа состоит из русской буквы (их 33) и двух цифр. Чему равна вероятность с первого раза набрать правильный шифр?

Решение: Воспользуемся формулой классической вероятности: .

Число исходов, благоприятствующих появлению данного события равно 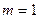. Число всевозможных исходов можно найти, воспользовавшись теоремой умножения в комбинаторике:

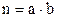
Здесь 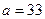, 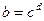размещение из 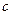по 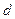с повторениями. В данном случае 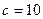, 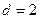. Таким образом:

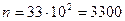
Искомая вероятность:

.

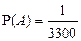Пример 8. Девять различных книг расставлены наудачу на одной полке. Найдите вероятность того, что четыре определенные книги окажутся поставленными рядом.

Решение

Здесь число всех исходов есть перестановка из 9 элементов 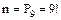. Подсчитаем число исходов m, благоприятствующих данному событию. Представим, что четыре определенные книги связаны вместе, тогда эту связку можно расположить на полке 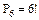способами (связка плюс остальные пять книг). Внутри связки четыре книги можно переставлять 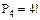способами. При этом каждая комбинация внутри связки, может сочетаться с каждым из 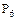способов образования связки, то есть 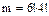. Следовательно

.

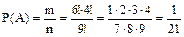Пример 9. В урне 10 белых, 15 черных, 20 синих, 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар: белый; черный; синий; красный; белый или черный; синий или красный; белый, черный или синий.

Решение.

Имеем ,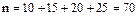

, , , .

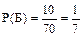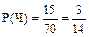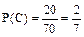Применив теорему сложения вероятностей, получим:

;

;

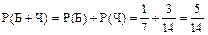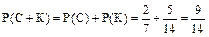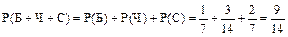или

.

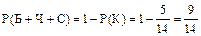Пример 10. На отрезке [0; 1] случайным образом выбираются две точки a и b. Какова вероятность того, что длина отрезка [a; b] окажется меньше ½?

Решение. Обозначим координаты точек a и b через x, y. Каждому выбору точек a, b поставим в соответствие точку на плоскости с координатами (x, y). Множеством всех возможных исходов являются точки квадрата со стороной, равной 1. Множеством благоприятных исходов те точки квадрата, для которых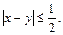

Считая все точки квадрата равновозможными, применим формулу

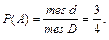
Дата добавления: 2014-11-29