
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула полной вероятности. Формула Байеса. Повторение испытаний. Формулы Бернулли, муавра-лапласа и Пуассона. Наивероятнейшее число успехов
|
|
|
|
Ответы
Задачи
1. Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна 0,8, вторым 0,8, третьим 0,9. Найти вероятность того, что все три стрелка поразят цель.
2. Экспедиция издательства отправляет газеты в два почтовых отделения. Вероятность доставки газет вовремя в каждое почтовое отделение равна 0,9. Найти вероятность того, что:
а) оба отделения почты получат газеты вовремя;
б) оба отделения почты получат газеты с опозданием;
в) хотя бы одно почтовое отделение получит газеты вовремя.
3. Рабочий обслуживает 3 станка. Вероятность того, что в течении 1 часа станок не потребует внимания рабочего равна для первого станка 0,9, для второго станка 0,8, для третьего станка 0,85. Найти вероятность того, что в течение некоторого часа ни один станок не потребует внимания рабочего.
4. В двух ящиках находятся детали. В первом 10 деталей, из них три стандартные, во втором 15 деталей, из них 6 стандартных. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными? Обе бракованными? Хотя бы одна стандартная?
5. В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу 2 пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
6. В одном ящике 5 белых и 10 красных шаров, в другом ящике 10 белых и 5 красных шаров. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
7. 12 служащих военного подразделения имеют профессию слесарей-сантехников, 9 из них имеют наивысший шестой разряд. Для монтажа оборудования на объект надо направить четырех высококвалифицированных слесарей, чтобы закончить работу в срок и качественно. Выбраны первые четверо военнослужащих по алфавитному списку. Какова вероятность того, что все четверо имеют шестой разряд?
8. В цехе 7 мужчин и 3 женщины. По табельным номерам наугад выбрали 3 человека. Какова вероятность того, что выбраны мужчины?
9. Из двух колод карт наудачу вынули по карте. Какова вероятность того, что обе карты пиковые?
10. Определить надежность двух дублирующих друг друга приборов. Надежность каждого равна p. При выходе из строя одного из них происходит мгновенное переключение на второй.
11. Экзаменующему преподавателю подан список группы из 26 человек. Известно, что 8 студентов в группе занимаются на “хорошо”. Наудачу из списка вызваны 2 студента. Найти вероятность того, что эти 2 студента хорошисты.
12. В барабане револьвера 7 гнезд, из них в 5 заложены патроны, а 2 оставлены пустыми. Барабан приводится во вращение, в результате чего против ствола случайным образом оказывается одно из гнезд. После этого нажимается спусковой крючок; если ячейка была пустая, то выстрела не происходит. Найти: а) вероятность того, что повторив такой опыт два раза подряд, мы оба раза не выстрелим, б) вероятность того, что оба раза выстрел произойдет.
13. Два стрелка сделали по одному выстрелу по мишени. Известно, что вероятность попадания в мишень для одного из стрелков равна 0,6, а для другого 0,7. Найдите вероятность того, что: а) только один из стрелков попадет в мишень; б) оба стрелка попадут в мишень; в) ни один из стрелков не попадет в мишень; г) хотя бы один из стрелков попадет в мишень.
14. Найти вероятность того, что наудачу взятое двухзначное число будет кратным либо 2, либо 5, либо тому и другому вместе.
15. Вероятность попадания в первую зону при одном выстреле равна 0,15, во вторую зону 0,2, в третью 0,3. Найти вероятность промаха.
16. Стрелок выбивает 10 очков с вероятностью 0,1, а 9 очков с вероятностью 0,3. Найти вероятность выбить не менее 9 очков.
17. Три стрелка попадают в мишень соответственно с вероятностью 0,9; 0,8; 0,7. Какова вероятность того, что при одном выстреле хотя бы один из них попадет в мишень?
18. Производится огневой налет на склады боеприпасов. Вероятность попадания в первый склад равна 0,05, во второй 0,08, в третий 0,15. При попадании хотя бы в один из складов происходит взрыв всех трех складов. Определить вероятность уничтожения всех трех складов.
19. Для оштукатуривания клуба было предложено использовать два насоса, один из которых имеет 60 % износа, второй 30 %. Насколько можно быть уверенным, что хотя бы один из насосов всегда будет в действии?
20. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, вторым 0,6. Найти вероятность того, что хотя бы один стрелок попал в мишень.
21. Три электролампочки последовательно включены в сеть. Вероятность того, что одна (любая) лампочка перегорит, если напряжение в сети превысит номинальное, равна 0,6. Найти вероятность того, что при повышении напряжения тока в цепи не будет.
22. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй 0,3, третий 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент услышит вызов радиста.
23. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить 4 бомбы, вероятности попадания которых равны 0,3, 0,4; 0,6; 0,7.
24. На стройке 4 автокрана. Для каждого автокрана вероятность того, что он работает в данный момент равна 0,8. Найти вероятность того, что в данный момент работает хотя бы один автокран.
25. Пусть вероятность того, что покупателю женской обуви потребуется обувь 37 размера равна 0,25. Найти вероятность того, что из четырех первых покупателей обувь этого размера:
а) никому не понадобится;
б) понадобится хотя бы одному.
26. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу выбранное изделие окажется высшего сорта равна 0,8. Найти вероятность того, что из трех проверенных изделий только два высшего сорта.
27. Вероятность попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле из первого орудия, если вероятность поражения цели из второго оружия равна 0,8.
28. Вероятность выигрыша по одному билету равна 1/7. Какова вероятность, купив 5 билетов, выиграть: а) по всем 5 билетам; б) ни по одному билету; в) хотя бы по одному билету.
29. В урне 5 белых, 7 черных шаров и 3 красных шара. Из этой урны один за другим вынимают все шары без возвращения и записывают их цвета. Найдите вероятность того, что в этом списке белый шар встретится раньше черного.
30. При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.
31. Студент успел подготовить к экзамену 20 вопросов из 25. Какова вероятность того, что из трех наудачу выбранных вопросов студент знает не менее двух?
32. Для одной торпеды вероятность попасть в корабль равна ½. Какова вероятность того, что 4 торпеды потопят корабль, если для его потопления достаточно одного попадания торпеды в цель.
33. Ящик содержит 90 годных и 10 дефектных деталей. Сборщик последовательно без возвращения достает из ящика 10 деталей. Найти вероятность того, что среди взятых деталей: а) нет дефектных; б) менее 3 дефектных.
34. В урне 2 белых и 4 черных шара. Два игрока достают из этой урны поочередно по одному шару, возвращая каждый раз извлеченный шар. Игра продолжается до появления белого шара. Определите вероятность того, что первым достанет белый шар начинающий игрок.
35. Решить предыдущую задачу в предположении, что шары не возвращаются в урну.
36. В урне 10 шаров. Вероятность того, что 2 извлеченных шара окажутся белыми, равна 2/15. Сколько в урне белых шаров?
37. В двух урнах находятся шары, причем в первой урне 5 белых шаров, 11 черных и 2 красных, а во второй соответственно 10, 8, 6. Из обеих урн наудачу извлекаются по одному шару. Какова вероятность того, что оба шара одного цвета.
38. Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый и второй вопросы билета, одинакова и равна 0,9; на третий 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить: а) на все 3 вопроса; б) хотя бы на 2 вопроса.
39. По результатам проверки контрольных работ оказалось, что в первой группе получили положительную оценку 20 студентов из 30, а во второй 15 из 25. Найти вероятность того, что наудачу выбранная работа, имеющая положительную оценку, написана студентом первой группы.
40. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе 0,9 и в третье 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б)хотя бы одно отделение получит газеты с опозданием.
41. Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. Вероятность безотказной работы в течение времени t первого узла равна 0,9, второго 0,95, третьего 0,8. Найти вероятность того, что в течение времени t прибор выйдет из строя.
42. Студент разыскивает нужную формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найти вероятность того, что эта формула содержится не менее, чем в двух справочниках.
43. Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,75; при втором 0,8; при третьем 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.
44. Вероятность своевременного выполнения студентом контрольной работы по каждой из трех дисциплин равна соответственно 0,6, 0,5 и 0,8. Найти вероятность своевременного выполнения контрольной работы студентом: а) по двум дисциплинам; б) хотя бы по двум дисциплинам.
45. Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй 0,6, третий 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.
46. Контролер ОТК, проверив качество сшитых 20 пальто, установил, что 16 из них первого сорта, а остальные – второго. Найти вероятность того, что среди взятых наудачу их этой партии трех пальто одно будет второго сорта.
47. Среди 20 поступающих в ремонт часов 8 нуждаются в общей чистке механизма. Какова вероятность того, что среди взятых одновременно наудачу 8 часов по крайней мере двое нуждаются в общей чистке механизма.
48. Среди 15 лампочек 4 стандартных. Одновременно берут наудачу 2 лампочки. Найти вероятность того, что хотя бы одна из них нестандартная.
49. В коробке смешаны электролампы одинакового размера и формы: по 100 Вт 7 штук, по 75 Вт 13 штук. Вытянуты наудачу 3 лампы. Какова вероятность того, что: а) они одинаковой мощности; б) хотя две из них по 100 Вт?
50. В коробке 10 красных, 3 синих и 7желтых карандашей. Наудачу вынимают 3 карандаша. Какова вероятность того, что они все: а) разных цветов; б) одного цвета?
51. Брак в продукции завода вследствие дефекта А составляет 4 %, а вследствие дефекта В 3,5 %. Годная продукция завода составляет 95 %. Найти вероятность того, что: а) среди продукции, не обладающей дефектом А, встретится дефект В; б) среди забракованной по признаку А продукции встретится дефект В.
52. Пакеты акций, имеющихся на рынке ценных бумаг, могут дать доход с вероятностью 0,5 (для каждого пакета). Сколько пакетов акций различных фирм нужно приобрести, чтобы с вероятностью, не меньшей 0,96875, можно было ожидать доход хотя бы по одному пакету акций?
53. Сколько раз нужно провести испытание, чтобы с вероятностью, не меньшей Р, можно было бы утверждать, что по крайней мере один раз произойдет событие, вероятность которого в каждом испытании равна р? Дать ответ при р = 0,4 и Р = 0,8704.
54. На полке стоят 10 книг, среди которых 3 книги по теории вероятностей. Наудачу берутся три книги. Какова вероятность, что среди отобранных хотя бы одна книга по теории вероятностей?
55. На связке 5 ключей. К замку подходит только один ключ. Найти вероятность того, что потребуется не более двух попыток открыть замок, если опробованный ключ в дальнейших испытаниях не участвует.
56. В магазине продаются 10 телевизоров, 3 из них имеют дефекты. Какова вероятность того, что посетитель купит телевизор, если для выбора телевизора без дефектов понадобится не более трех попыток?
| 72/125 | 12 а | 1/21 | 0,95 | 48 а | 0,282 | ||||
| 2 а | 0,81 | 12 б | 10/21 | 0,9984 | 0,347 | 48 б | 0,270 | ||
| 2 б | 0,01 | 13 а | 0,46 | 25 а | 0,36 | 0,636 | 49 а | 0,184 | |
| 2 в | 0,99 | 13 б | 0,42 | 25 б | 0,64 | 39 а | 0,032 | 49 б | 0,137 |
| 0,612 | 13 в | 0,12 | 0,384 | 39 б | 0,316 | 50 а | 0,0104 | ||
| 4 а | 3/25 | 13 г | 0,88 | 0,7 | 0,316 | 50 б | 0,625 | ||
| 4 б | 21/50 | 0,6 | 28 а | 1/75 | 0,788 | Не < 5 пакетов | |||
| 4 в | 29/50 | 0,204 | 28 б | (6/7)5 | 42 а | 0,54 | 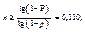 при р=0,4, р=0.8704, n³4 при р=0,4, р=0.8704, n³4
| ||
| 0,5 | 0,4 | 5/12 | 42 б | 0,995 | 0,708 | ||||
| 7/9 | 0,994 | 43 а | 0,46 | 0,4 | |||||
| 14/55 | 0,126 | 43 б | 0,7 | 0,992 | |||||
| 7/24 | 0,72 | 15/16 | 0,982 | ||||||
| 1/16 | 0,88 | 0,421 | |||||||
| (1-p)2 | 0,936 | 3/5 | 0,344 | ||||||
| 28/325 | 0,664 | 2/3 | 0,476 |
Студент должен знать:
- формулу полной вероятности и формулу Байеса;
- формулу Бернулли, Муавра –Лапласа и Пуассона;
Студент должен уметь:
- находить вероятность событий, используя формулы полной вероятности, Байеса, Бернулли, Муавра –Лапласа и Пуассона,
- находить наивероятнейшее число успехов.
Литература: [5] стр.44-59.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 2408; Нарушение авторских прав?; Мы поможем в написании вашей работы!