Основные теоретические сведения. - понятие случайной величины и ее виды;

РЯД РАСПРЕДЕЛЕНИЯ. ИНТЕГРАЛЬНАЯ И ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ.

Студент должен знать:

- понятие случайной величины и ее виды;

- способы задания случайной величины;

- закон распределения случайной величины;

Студент должен уметь:

- строить ряд распределения случайной величины;

- находить функцию распределения случайной величины.

Литература: [5] стр.60-72.

Величина, которая в результате опыта может принимать те или иные значения называются случайной величиной. Например, время ожидания автобуса на остановке, число свободных мест в вагоне поезда и т. д. Обозначать случайные величины будем заглавными латинскими буквами X, Y, Z и т. д.

Случайная величина называется дискретной, если мы можем перечислить все ее возможные значения и указать вероятность каждого значения.

Возможных значений может быть бесконечно много. Обычная дискретная величина задается рядом распределения в виде следующей таблицы.

X				...
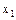
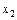
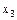
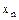
P				...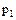

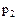
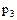
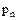
Здесь, 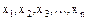- все возможные различные значения случайной величины, а 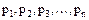- вероятности, с которой случайная величина принимает соответствующие значения,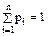

Не всегда можно задать случайную величину, указав вероятность каждого отдельного значения. В ряде случаев вероятность каждого отдельного значения равна 0. Любую случайную величину можно задать, указав ее функцию распределения.

Функция F(x)=P(X<x) называется интегральной функцией распределения случайной величины X или просто функцией распределения.

Функция распределения обладает следующими свойствами.

1. Монотонностью, то есть, если 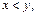то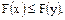

2. Для любых 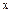справедливо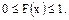

3.

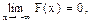
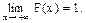
С помощью функции распределения можно подсчитать вероятность попадания случайной величины Х в интервал [a, b).

Назовем случайную величину непрерывной, если непрерывна ее функция распределения F(x).

Заметим, что в этом случае вероятность каждого значения случайной величины равна нулю.

Будем считать, что существует функция 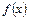такая, что

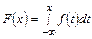при всех .

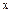В этом случае функцию 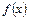назовем плотностью распределения случайной величины Х или дифференциальной функцией распределения. Справедливо равенство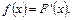

Вероятность попадания случайной величины Х в интервал (а,b) можно посчитать по формуле .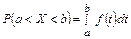

Свойство плотности распределения .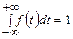

Дата добавления: 2014-11-29