Дискретные и непрерывные случайные величины

Ответы

Задачи

1. Имеется 2 одинаковых ящика с шарами. В первом ящике 2 белых и 1 черный шар, во втором 1 белый и 4 черных шара. Наудачу выбирают один ящик и вынимают из него шар. Какова вероятность того, что вынутый шар окажется белым?

2. Из урны, в которой находилось 5 белых и 6 черных шаров, потерялся один шар неизвестного цвета. Из урны извлечен наудачу один шар. Какова вероятность того, что вынутый шар окажется белым?

3. В цехе работают 20 станков. Из них 10 марки А, 6 марки В и 4 арки С. Вероятность того, что качество детали окажется отличным равна 0,9; 0,8; 0,7 соответственно. Какой процент отличных деталей выпускает цех в целом?

4. С первого станка-автомата на сборку поступают 40 %, со второго 30 %, а с третьего 20 %, с четвертого 10 % деталей. Среди деталей, выпущенных первым станком 2 % бракованных, вторым 1 %, третьим 0,5 %, четвертым 0,2 %. Найдите вероятность того, что поступившая на сборку деталь не бракованная.

5. Имеются 2 урны: в первой 3 белых шара и 2 черных; во второй 4 белых и 4 черных. Из первой урны во вторую перекладывают, не глядя, 2 шара. После этого из второй урны берут один шар. Какова вероятность того, что он белый?

6. Предположим, что 5 % всех мужчин и 0,25 % женщин – дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина?

7. На некоторой фабрике машина А производит 40 % всей продукции, а машина В 60 %. В среднем 9 единиц из 1000 единиц продукции, произведенной машиной А, оказывается браком, а у машины В брак 2 единицы из 500. Некоторая единица продукции, выбранная случайным образом из дневной продукции, оказалась браком. Какова вероятность того, что она произведена на машине В?

8. В первой урне находится один белый и 9 черных шаров, а во второй – 1 черный и 5 белых шаров. Из каждой урны удалили случайным образом по одному шару, а оставшиеся шары ссыпали в третью (свободную) урну. Найти вероятность вынуть белый шар из третьей урны.

9. Имеется две партии изделий по 10 и 12 штук, причем в каждой партии одно бракованное. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.

10. Для контроля продукции из трех партий деталей взята для испытания одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других все доброкачественные.

11. В первой урне содержится 10 шаров, из них 8 белых; во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих шаров наудачу взят один шар. Найдите вероятность того, что взят белый шар.

12. Два стрелка независимо друг от друга стреляют по одной мишени, делая по одному выстрелу. Вероятность попадания в мишень первого стрелка 0,8; для второго 0,4. Найдите вероятность того, что в мишень попал первый стрелок, если в мишени обнаружена одна пробоина.

13. На фабрике, изготовляющей болты, первая машина производит 25 %, вторая 35 % и третья 40 % всех изделий. В их продукции брак составляет 5, 4 и 2 % соответственно. а) Какова вероятность того, что случайно выбранный болт будет дефективным? б) Если болт дефективный, то какова вероятность того, что он изготовлен первой, второй или третьей машиной?

14. Туристы вышли из пункта О, выбирая наугад на разветвлении дорог один из возможных путей. Какова вероятность того, что они попадут в пункт А?

Рисунок 2. Рисунок 3.

15. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 с вероятностью 0,7; 4 с вероятностью 0,6 и 2 с вероятностью 0,5. Наудачу выбранный стрелок не попал в цель. К какой группе вероятнее всего принадлежал этот стрелок?

16. На трех дочерей – Алису, Марину и Елену в семье возложена обязанность мыть посуду. Поскольку Алиса старшая, ей приходится выполнять 40 % всей работы. Остальные 60 % работы Марина и Елена делят поровну. Когда Алиса моет посуду, вероятность для нее разбить что-либо равна 0,02. Для Марины и Елены эта вероятность равна соответственно 0,03 и 0,04. Родители не знают, кто мыл посуду вечером, но они слышали звон разбитой тарелки. Какова вероятность того, что посуду мыла Алиса? Марина? Елена?

17. В каждой из трех урн по 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую, после чего из второй урны наудачу извлечен один шар и переложен в третьюу. Найти вероятность того, что шар, извлеченный затем из третьей урны, окажется белым.

18. В группе из 20 стрелков имеется 4 отличных, 10 хороших и 6 непосредственных стрелков. Вероятность попадания в цель при одном выстреле для отличного стрелка равна 0,9; для хорошего 0,7; для посредственного 0,5. Найдите вероятность того, что: а) наудачу выбранный стрелок попадет в цель; б) 2 наудачу выбранных стрелка попадут в цель.

19. Четыре стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятности попадания для данных стрелков равны 0,4; 0,6; 0,7; 0,8. После стрельбы в мишени обнаружены 3 пробоины. Найдите вероятность того, что промахнулся четвертый стрелок.

20. Три автомата изготавливают детали, которые поступают на общий конвейер. Производительность автоматов относятся 2: 3: 5. Вероятность того, что деталь изготовлена на первом автомате отличного качества, равна 0,9, для второго 0,8, для третьего 0,7. Найти вероятность того, что наудачу взятая с конвейера деталь окажется отличного качества.

21. Число грузовых автомашин, проезжающих по шоссе мимо бензоколонки относится к числу легковых машин этого же направления как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; легковая 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.

22. У рыбака есть три излюбленных места рыбалки, которые он посещает с одинаковой вероятностью. Вероятность клева на первом месте равна 1/4, на втором 1/3, на третьем 1/2. Рыбак забросил удочку, и рыба клюнула. Найти вероятность того, что он удил на первом месте.

23. У рыбака есть три излюбленных места рыбалки, которые он посещает с одинаковой вероятностью. Вероятность клева на первом месте 1/3, на втором месте 1/2, на третьем месте равна 1/4. Рыбак забросил удочку 3 раза, и рыба клюнула 1 раз. Найти вероятность того, что он удил рыбу на первом месте.

24. Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность среди пяти случайно выбранных волокон смеси обнаружить менее двух окрашенных?

25. Изделия некоторого производства содержат 5 % брака. Найти вероятность того, что среди пяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных.

26. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их количество равно 7.

27. Батарея дала четырнадцать выстрелов по объекту, вероятность попадания в который равна 0,2. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.

28. Что вероятнее, выиграть у равносильного противника: 1) три партии из четырех или пять из восьми; 2) не менее трех партий из четырех или не менее пяти партий из восьми?

29. Вероятность попадания в цель при каждом выстреле из орудия равна 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20?

30. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех?

31. Вероятность того, что лампа останется исправной после 1000 часов работы, равна 0,2. Какова вероятность того, что хотя бы одна из трех ламп останется исправной после 1000 часов работы?

32. Контрольное задание состоит из 5 вопросов, на каждый из которых дается 4 варианта ответа, причем один из них правильный, а остальные неправильные. Найдите вероятность того, что учащийся, не знающий ни одного вопроса, дает: а) 3 правильных ответа, б) не менее 3 правильных ответов (предполагается, что ответы учащийся выбирает наудачу).

33. Проведено 5 независимых испытаний, каждое из которых состоит в одновременном подбрасывании 2 монет. Найдите вероятность того, что ровно в трех испытаниях появилось по два герба.

34. Вероятность рождения мальчика равна 0,515, девочки – 0,485. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек?

35. На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой из них равна 0,8. Найдите вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не менее 8 автомашин.

36. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено изделий а) ровно 3, б) менее 3, в) более 3.

37. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно 2; б) менее 2; в) более 2.

38. Вероятность рождения мальчика 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.

39. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

40. Вероятность поражения мишени стрелком при одном выстреле p = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.

41. Найти вероятность того, что при 400 испытаниях событие наступит 104 раза, если вероятность его появления в каждом испытании равна 0,2.

42. Прядильщик обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение одной минуты 0,004. Найти вероятность того, что в течение одной минуты обрыв произойдет в 5 веретенах.

43. Коммутатор учреждения обслуживает 100 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,02. Какое из двух событий вероятнее в течение одной минуты: позвонит 3 абонента, позвонит 4 абонента?

44. Вероятность рождения мальчика равна 0,5. Найдите вероятность того, что среди 200 новорожденных детей будет: а) 100 мальчиков; б) 90 мальчиков; в) 110 мальчиков; г) от 90 до 110 мальчиков.

45. Вероятность того, что покупателю потребуется обувь 41 размера, равна 0,2. Найдите вероятность того, что из 100 покупателей потребует обувь 41 размера: а) 25 человек; б) от 10 до 30 человек; в) не более 30 человек; г) не менее 35 человек.

46. 100 станков работают независимо друг от друга, причем вероятность бесперебойной работы каждого из них в течении смены равна 0,8. Найдите вероятность того, что в течении смены бесперебойно проработают: а) 85 станков; б) от 75 до 85 станков.

47. Вероятность выхода из строя за время t одного конденсатора равна 0,2. Найдите вероятность того, что за время t из 100 независимо работающих конденсаторов выйдут из строя: а) не менее 20 конденсаторов; б) менее 28 конденсаторов; в) от 14 до 26 конденсаторов.

48. Завод отправил на базу 5000 доброкачественных изделий. Вероятность повреждения каждого изделия в пути равна 0,0002. Найдите вероятность того, что среди 5000 изделий в пути будет повреждено:

а) 3 изделия; б) 1 изделие; в) не более 3 изделий; г) более 3 изделий.

49. Вероятность появления события в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

50. Какова вероятность того, что в столбике из 100 наугад отобранных монет число монет, лежащих «гербом» вверх, будет от 45 до 55.

51. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание.

52. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным, равна 0,6. Найти наивероятнейшее число образцов, которое товаровед признает годными.

53. Два стрелка одновременно стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка 0,8, а для второго 0,6. Найти наивероятнейшее число залпов, при которых оба стрелка попадут в мишень, если будет проведено 15 залпов.

54. Вероятность появления события в каждом из испытаний равна 0,3. Найти число испытаний n, при котором наивероятнейшее число появлений события в этих испытаниях будет равно 30.

55. Страховая компания разделяет застрахованных по классам риска: I класс – малый риск, II класс – средний, III класс – большой риск. Среди этих клиентов 50 % первого класса риска, 30 % второго и 20 % третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса риска равна 0,01, второго 0,03, третьего 0,08. Какова вероятность того, что: а) застрахованный получит денежное вознаграждение за период страхования; б) получивший денежное вознаграждение застрахованный относится к группе малого риска?

56. В данный район изделия поставляются тремя фирмами в соотношении 5: 8: 7. Среди продукции первой фирмы стандартные изделия составляют 90 %, второй 85 %, третьей 75 %. Найти вероятность того, что приобретенное изделие окажется: а) нестандартным; б) стандартным. Какова вероятность того, что оно изготовлено третьей фирмой?

57. Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго 0,3. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежала первому стрелку.

58. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55 % изделий, а второй остальные. Вероятность того, что первый контролер пропустил нестандартное изделие, равна 0,01, второй 0,02. Взятое наудачу изделие, маркированное как стандартное, оказалось нестандартным. Найти вероятность того, что изделие проверялось вторым контролером.

59. Вероятность изготовления изделия с браком на данном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае бездефектного изделия пропускает его с вероятность 0,96, а в случае изделия с дефектом с вероятностью 0,05. Определить: а) какая часть изготовленных изделий выходит с предприятия? б) какова вероятность того, что изделие, выдержавшее упрощенную проверку, бракованное?

60. В одной урне 5 белых и 6 черных шаров, а в другой 4 белых и 8 черных шаров. Из первой урны случайным образом вынимают 3 шара и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шара. Найти вероятность того, что все шары, вынутые из второй урны, белые.

61. Из п экзаменационных билетов студент А подготовил только т (т < n). В каком случае вероятность вытащить на экзамене «хороший» для него билет выше: когда он берет наудачу первым или вторым, …, или k – м (k < n) по счету среди сдающих экзамен?

62. Вероятность малому предприятию быть банкротом за время t равна 0,2. Найти вероятность того, что из восьми малых предприятий за время t сохраняться: а) два; б) более двух.

63. В среднем пятая часть поступающих в продажу автомобилей некомплектны. Найти вероятность того, что среди десяти автомобилей имеют некомплектность: а) три автомобиля; б) менее трех.

64. Производится залп из 6 орудий по объекту. Вероятность попадания в объект из каждого орудия равна 0,6. Найти вероятность ликвидации объекта, если для этого необходимо не менее четырех попаданий.

65. В среднем по 15 % договора страхования компания выплачивает сумму. Найти вероятность того, что из десяти договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров.

66. Предполагается, что 10 % открывающихся малых предприятий прекращают свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?

67. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье: а) не менее трех мальчиков; б) не более трех мальчиков.

68. Два равносильных противника играют в шахматы. Что более вероятно: а) выиграть 2 партии из 4 или 3 партии из 6? б) не менее 2 партий из 6 или не менее 3 партий из 6? (Ничья в расчет не принимается).

69. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакете недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) 3 ошибочно укомплектованных пакета; б) не более трех пакетов.

70. Строительная фирма, занимающаяся сборкой летних коттеджей, раскладывает рекламные листки по почтовым ящикам. Опыт работы компании показывает, что примерно в одном случае из двух тысяч следует заказ. Найти вероятность того, что при размещении 100 тыс. листков число заказов будет: а) равно 48; б) находиться в границах от 45 до 55.

71. В вузе обучаются 3650 студентов. Вероятность того, что день рождения студента приходится на определенный день года, равна 1/365. Найти а) наиболее вероятное число студентов, родившихся 1 мая, и вероятность такого события; б) вероятность того, что, по крайней мере, 3 студента имеют один и тот же день рождения.

72. Учебник издан тиражом 10000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован неправильно, равна 0,0001. Найти вероятность того, что а) тираж содержит 5 бракованных книг; б) по крайней мере 9998 книг сброшюрованы правильно.

73. Два баскетболиста делают по 3 броска мячом в корзину. Вероятности попадания мяча в корзину при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что: а) у обоих будет одинаковое количество попаданий; б) у первого баскетболиста будет больше попаданий, чем у второго.

74. Известно, что в среднем 60 % всего числа изготовляемых заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии окажется: а) 6 аппаратов первого сорта, если партия содержит 10 аппаратов; б) 120 аппаратов первого сорта, если партия содержит 200 аппаратов?

75. Вероятность того, что перфокарта набита оператором неверно, равна 0,1. Найти вероятность того, что: а) из 200 перфокарт правильно набитых будет не меньше 180; б) у того же оператора из десяти перфокарт будет неверно набитых не более двух.

76. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 50 % студентов. Найти вероятность того, что из 400 студентов работу успешно выполнят: а) 180 студентов, б) не менее 180 студентов.

77. При обследовании уставных фондов банков установлено, что пятая часть банков имеют уставный фонд свыше 100 млн. руб. найти вероятность того, что среди 1800 банков имеют уставный фонд свыше 100 млн. руб.: а) не менее 300; б) от 300 до 400 включительно.

78. Сколько нужно взять деталей, чтобы наивероятнейшее число годных деталей было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1?

79. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,01. Найти наиболее вероятное число опоздавших из 800 пассажиров и вероятность такого числа опоздавших.

80. Вероятность того, что деталь стандартна, равна 0,9. Найти: а) с вероятностью 0,9545 границы, в которых заключена доля стандартных среди проверенных 900 деталей; б) вероятность того, что доля стандартных деталей среди них заключена в пределах от 0,8 до 0,11.

81. В результате проверки качества приготовленных для посева семян гороха установлено, что в среднем 90 % всхожи. Сколько нужно посеять семян, чтобы с вероятностью 0,991 можно было ожидать, что доля взошедших семян отклонится от вероятности взойти каждому семени не более, чем на 0,03 (по абсолютной величине)?

82. Вероятность того, что дилер, торгующий ценными бумагами, продаст их, равна 0,7. Сколько должно быть ценных бумаг, чтобы можно было утверждать с вероятностью 0,996, что доля проданных среди них отклонится от 0,7 не более, чем на 0,04 (по абсолютной величине)?

83. У страховой компании имеются 10000 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 500 руб. Вероятность несчастного случая 0,0055, а страховая сумма, выплачиваемая пострадавшему, составляет 50000 руб. Какова вероятность того, что: а) страховая компания потерпит убыток; б) на выплату страховых сумм уйдет более половины всех средств, поступивших от клиентов?

	13/30					37 а	0,224
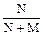
			ко второй		24, 25	37 б	0,1992	49 а	0,89
	0,83					37 в	0,5769	49 б	0,89
							0,0782	49 в	0,11
	0,52						0,0498		0,68
	20/21		0,088	32 а	0,088		0,273
			0,77	32 б	0,104		0,0006		14, 15
	38/105		3/7		0,088		0,1562
			3/13				первое		100, 101
			256/715
				36 а	0,0613
	6/17			36 б	0,9197
				36 в	0,019

Дата добавления: 2014-11-29