Примеры. Пример 1. Имеется 10 деталей, из них 6 стандартные

Пример 1. Имеется 10 деталей, из них 6 стандартные. Составить ряд распределения числа стандартных деталей из двух выбранных.

Решение: Очевидно, что при выборе двух деталей, число стандартных деталей может оказаться равным 0, 1, 2, то есть мы имеем дело с дискретной случайной величиной. Найдем вероятность, с которой принимается каждое значение, и составим ряд распределения. Считаем, что выбор каждой детали равновозможен, и применим для нахождения вероятностей классическое определение.

Число всех возможных исходов для выбора двух исправных деталей равно .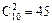

Число благоприятных вариантов для выбора только нестандартных деталей равно .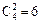

Число благоприятных вариантов для выбора одной исправной детали равно .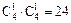

Число благоприятных вариантов для выбора только стандартных деталей равно .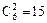

Таким образом,

Составим ряд распределения.

Х
Р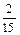

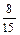
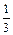
Для проверки убедимся, что сумма вероятностей равна 1.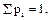

Пример 2. В партии из семи деталей четыре окрашенные. Наудачу взяты три детали. Построить ряд и многоугольник распределения случайной величины 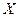- числа окрашенных деталей среди отобранных.

Решение: Случайная величина 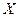может принять следующие четыре значения: 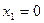, , 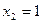, 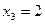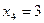. Вероятности этих значений равны:

, ,

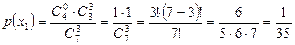
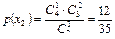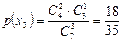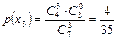
Складывая полученные вероятности, имеем:

.

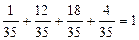Составим ряд распределения:

x
p	1/35	12/35	18/35	4/35

Построим многоугольник распределения случайной величины Х (рис.4).

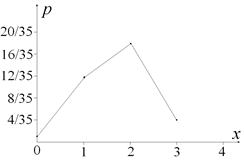
Рисунок 4. Многоугольник распределения

Пример 3. Найти интегральную функцию распределения случайной величины Х, заданной рядом распределения. Построить ее график.

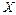
	-1
p	0,1	0,4	0,5

Решение. Чтобы найти вероятность события Х< x, разобьем числовую ось 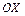на интервалы точками – 1, 0 и 2. Если 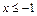, то событие 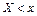невозможно и в этом случае 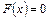. Если 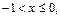то событие имеет место тогда и только тогда, когда 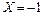, то есть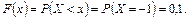

-1 0 2 х

Если 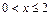, то событие может произойти только в том случае, если Х = -1 или Х = 0, то есть

И, наконец, если , то событие достоверно и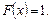

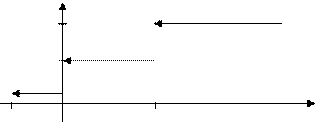
На координатной плоскости построим график (рис.4).

F(x)

0,5

0,1

-1 0 2 x

Рисунок 5. График интегральной функции распределения

Пример 4. Дискретная случайная величина Х задана законом распределения

X
p	0,3	0,1	0,6

Найти функцию распределения и начертить ее график.

Решение: Если 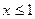, то 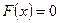, поскольку случайная величина не принимает значений меньших 1.

Если 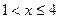, то .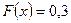

Если 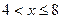, то 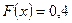– на этом интервале принимает значение 1 с вероятностью 0,3 и значение 4 с вероятностью 0,1. Поскольку эти события несовместны, то по теореме сложения вероятностей 0,3 + 0,1 = 0,4.

Если , то .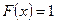

Итак, функция распределения аналитически может быть записана так:

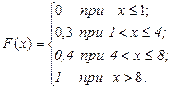
График данной функции:

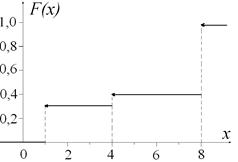
Рисунок 5. График функции распределения.

Пример 5. Найти функцию плотности непрерывной случайной величины, заданной функцией распределения

Построить графики функций F(x) и f(x). Найти вероятность попадания в интервал .

Решение. Найдем дифференциальную функцию распределения (функцию плотности):

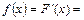
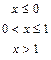
Построим график функции распределения (рис. 6) и график дифференциальной функции распределения (рис. 7)

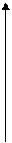F(x)

1

0 1 x

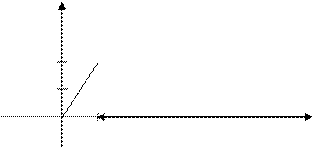Рисунок 6. График интегральной функции распределения

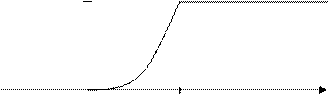
f(х)

0 1 х

Рисунок 7. График дифференциальной функции распределения

Найдем вероятность попадания случайной величины 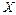в интервал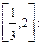

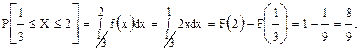
Пример 6. Случайная величина Х задана функцией распределения:

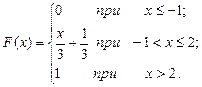
Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0,1).

Решение: Вероятность того, что 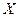примет значение, заключенное в интервале 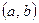, равна приращению функции распределения на этом интервале .

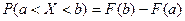Положив 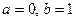, получим:

Пример 6. Разыгрываются две вещи стоимостью по 150 рублей и одна вещь стоимостью 300 рублей. Составьте закон распределения выигрышей, купившего 1 билет из 50.

Решение. Искомая случайная величина Х представляет собой выигрыш и может принимать три значения: х₁ = 0, х₂ = 150 и х₃ = 300 рублей.

Первому результату благоприятствует 47 случаев, второму результату – два случая и третьему – один случай. Найдем их вероятности:

; ; .

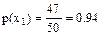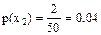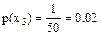Закон распределения случайной величины имеет вид:

Значения xi
Вероятности pi	0.94	0.04	0.02

В качестве проверки найдем

.

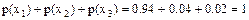Дата добавления: 2014-11-29