Примеры. Пример 1. Опыт заключается в трехкратном подбрасывании игральной кости

Пример 1. Опыт заключается в трехкратном подбрасывании игральной кости. Найти вероятность, что все три раза выпадет 6 очков.

Решение. Вероятность выпадения 6 очков равна 1/6 и все броски независимы в совокупности. Поэтому применима формула Бернулли. Здесь число опытов n = 3, успехом будем считать выпадение 6 очков. Вероятность успеха в одном опыте p = 1/6, вероятность неуспеха q = 5/6. Число успехов может быть любым от 0 до 3.

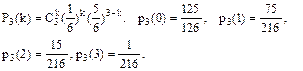
Для проверки желательно убедиться в том, что сумма всех вероятностей равна 1.

Пример 2. Футболист выполняет пенальти. Вероятность того, что он забьет гол равна 0,8. Найти вероятность того, что из серии 5 пенальти данный футболист забьет 3 мяча.

Решение: Воспользуемся формулой Бернулли:

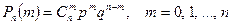
Найдем сначала число сочетаний:

.

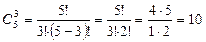
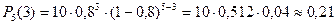Пример 3. Монета брошена 2N раз. Найти вероятность того, что герб выпадет ровно N раз.

Решение. Имеем схему Бернулли, в которой количество испытаний n=2N. Вероятность успеха (выпадение «герба») в одном испытании p=0,5. Тогда вероятность неуспеха (выпадение «решки») в одном испытании q=1-p=0,5. По условию количество успехов (количество выпадений герба) k=N.

При этом возможны два случая:

1 случай. Небольшое количество опытов. Тогда используем формулу Бернулли

.

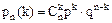Например, N=3, тогда

.

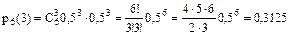2 случай. Большое количество опытов (при большой вероятности успеха). Тогда используем локальную формулу Муавра-Лапласа.

.

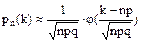В нашем случае, имеем

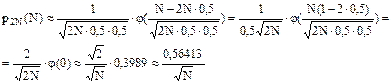
По таблице приложения 1 (стр.79) находим, что φ(0)=0,3989.

Например, при N=100, имеем .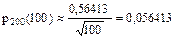

Пример 4. Найти вероятность того, что событие 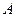наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение: Воспользуемся локальной теоремой Лапласа:

, .

, , , .

.

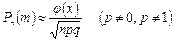
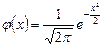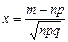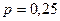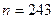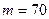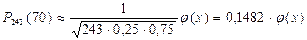Найдем значение аргумента .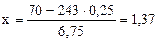

По таблице приложения 1 (стр.79) находим 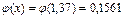. Искомая вероятность равна:

.

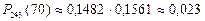Пример 5. Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение года равна 0,002. Какова вероятность отказа: а) двух элементов за год? б) не менее двух элементов за год?

Решение. Будем рассматривать работу каждого элемента как отдельное испытание. Обозначим А – «Отказ элемента за год».

P(A)=p=0,002; np=1000*0,002=2 < 9

а) Значит, вероятность отказа двух элементов за год найдем по формуле Пуассона: так как 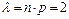, 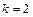(количество отказавших элементов). Тогда по таблице приложения 3 (стр. 81) находим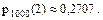

б) Обозначим через 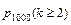– вероятность отказа не менее двух элементов за год. Вычислим 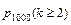, как вероятность противоположного события к событию 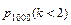, то есть:

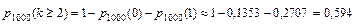
Так как (, ),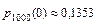

(, ).

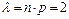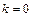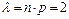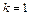Пример 6. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий:

В – наудачу взятая коробка содержит 13 бракованных изделий;

С – число бракованных изделий в коробке не превосходит 20

Решение. Изготовление детали – это испытание, в котором может появиться событие А – изделие бракованное – с вероятностью p=0,15. Находим np =15, npq =12,75. Можно применять формулы Лапласа:

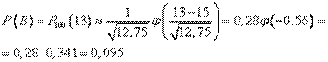
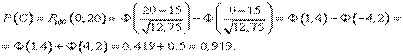
Приблизительно 9,5% всех коробок содержат 13 бракованных изделий и в 92% коробок число бракованных не превосходит 20.

Пример 6. Вероятность того, что деталь не прошла проверку ОТК равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100.

Решение. Из условия задачи имеем p = 0.2, q = 0.8, n = 400, m₁ = 70, m₂ = 100. Тогда

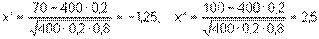
По интегральной формуле Муавра – Лапласа имеем

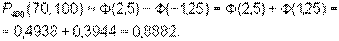
Пример 7. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.

Решение. Здесь n=50, p=0,9, q=1 − p = 1 − 0,9 = 0,1. Поэтому имеем неравенства:

50·0,9 − 0,1 ≤ k ≤ 50·0,9 + 0,1$

44,9 ≤ k ≤ 45,9

Следовательно, k = 45.

Пример 8. Данные проверки качества выпускаемых стандартных деталей показали, что в среднем брак составляет 7,5%. Определить наиболее вероятное число вполне исправных деталей в партии из 39 штук.

Решение. Получение бракованной детали и получение исправной детали — события противоположные. Обозначая вероятность выпуска исправной детали через p, будем иметь q=1 − p = 1 − p=0,075 (так как брак составляет 7,5%). Следовательно p=1-0,075=0,925. Так как здесь n= 39, то искомое число можно найти из неравенств:

39·9,925−0,075 ≤ k ≤ 39·0,925+0,925$

36 ≤ k ≤ 37.

Отсюда наивероятнейшее число исправных деталей равно 36 или 37.

Дата добавления: 2014-11-29