Описание моделируемого объекта

Теоретическое введение. Моделирование с использованием конечных автоматов

Дискретная модель элемента. Конечный автомат

Лабораторная работа N№ 4

Конечные автоматы и такие тесно связанные с ними конструк­ции, как, например, линейные грамматики и регулярные выраже­ния, относятся к важнейшим основным понятиям информатики. Различные варианты конечных автоматов и близкие им матема­тические объекты служат для описания и анализа технических уст­ройств, различных систем и процессов, программ и алгоритмов. Многие сложные концепции теоретической информатики — и при­том относящиеся не только к более общим моделям автоматов, таким как автоматы с магазинной памятью и машины Тьюрин­га, — были выработаны на базе теории конечных автоматов. Тео­рия автоматов порождает ряд легко формулируемых, но далеко не тривиальных проблем. Они приводят к весьма сложным алго­ритмам и отчасти проясняют причины, по которым необходимо систематическое развитие математического программирования и теории алгоритмов, сопровождаемое подробным анализом коррект­ности и сложности. Теория конечных автоматов имеет многочис­ленные приложения в технической и практической информатике и составляет существенную часть теоретической информатики. Это делает знание методов моделирования на основе теории автоматов необходимым каждому спе­циалисту по информатике.

В силовой установке требуется постоянно контро­лировать направление вращения цилиндрического вала с помощью автономно работающего прибора. Этот прибор должен в опреде­ленные моменты времени выдавать соответствующий направлению вращения вала сигнал, который далее может использоваться в дру­гих звеньях системы управления.

Допустим, что в качестве датчика на конце вала закреплена изолированная от него шайба, разделенная на четыре сектора, из которых одна пара противоположных секторов сделана проводя­щей, а другая — непроводящей. Пусть также у свободной стороны шайбы расположен скользящий контакт (щетка), который держит шайбу под постоянным напряжением. Два других скользящих кон­такта 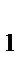X и X 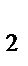размещены так, что они касаются края шайбы и про­бегают при ее вращении выделенные секторы один за другим, и, кроме того, могут одновременно находиться в пределах наимень­шего из секторов. Напряжения на контактах 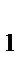X и X 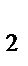рассматри­ваются как входы конструируемого автомата A, и считается, что эти входы (при соответствующем нормировании) принимают зна­чения 0 и 1. В качестве выхода автомата A можно использовать напряжение 1, если шайба вращается по часовой стрелке, и на­пряжение 0, если она вращается в противоположном направлении (рис. 7).

Рис. 7. Индикатор

Техническая реализация прибора далее обсуждаться не будет. Скажем только, что в системе предполагается наличие датчика тактов, устанавливающего моменты времени, в которые автомат A воспринимает входы и вырабатывает соответствующий выход. Следует отметить, что промежутки времени, в течение которых из­меряются напряжения на контактах, должны быть очень коротки­ми по сравнению с периодом вращения.

Дата добавления: 2014-11-28