Анализ поведения динамического элемента. Аналитическая реализация непрерывной линейной математической модели

Аналитическая реализация непрерывной линейной математической модели

При моделировании динамического элемента с запаздыванием необходимо провести моделирование ДЭ без запаздывания и моделирование запаздывания, как некоторой единой системы. Часто для идеального запаздывания используют передаточную функцию:

, где 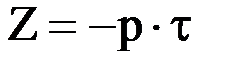. (55)

Моделирование запаздывания может осуществляться с помощью предельных переходов, степенных и специальных рядов.

Предельные переходы:

а)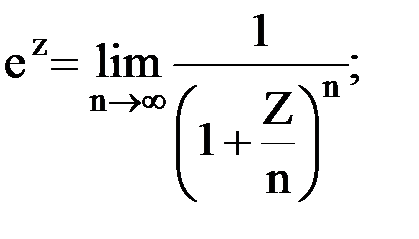

б)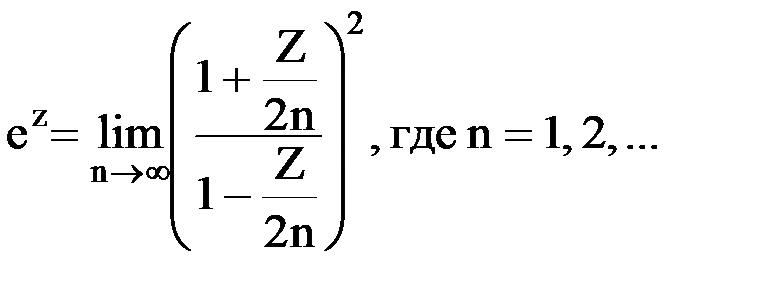

Степенной ряд:

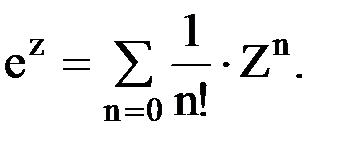
Специальный ряд:

ряд Падэ:

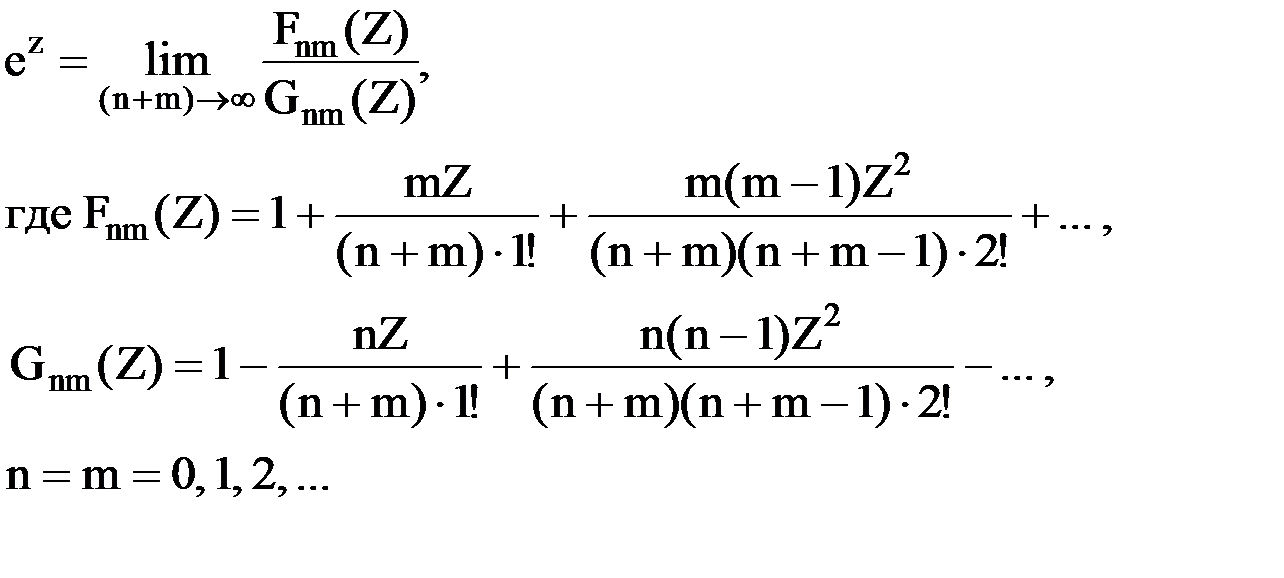
Если n = m = 1, то в области оригиналов получаем дифференциальное уравнение первого порядка, если же n = m = 2, то получаем дифференциальное уравнение второго порядка.

Используем в качестве математической модели запаздывания разложение в ряд Падэ.

В случае n = m = 0 имеем вырожденный случай, когда никакого запаздывания нет, т.е. W (p) = 1. В случае n = m = 1 имеем

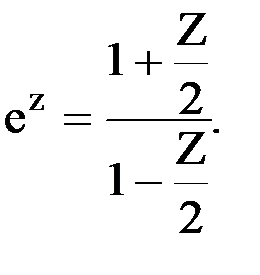
Т.к. Z = p, то

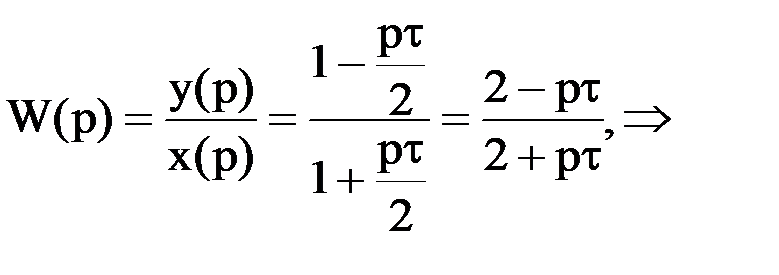
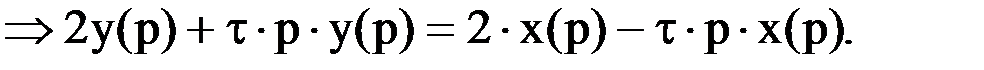
Переходя к оригиналам и полагая y(0) = 0 и x(0) = 0, имеем

.

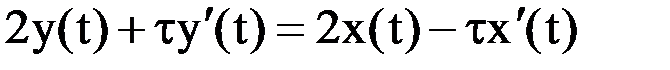Поскольку x(t) = Сonst = k, то 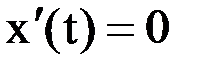и, следовательно, данное уравнение преобразуется к следующему виду:

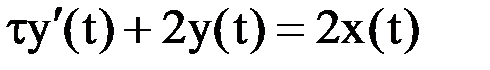или .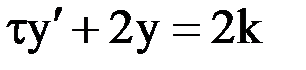

Уравнение 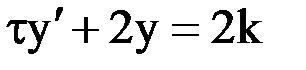является линейным неоднородным дифференциальным уравнением первого порядка с постоянными коэффициентами. Его решение ищем в ви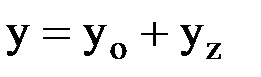де , где 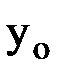— решение соответствующего однородного дифференциального уравнения, а 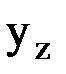— частное решение данного уравнения.

Характеристическое уравнение имеет вид:

.

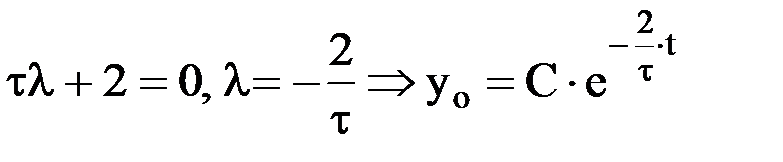Нетрудно видеть, что решение y = k является частным решением данного уравнения. Таким образом,

.

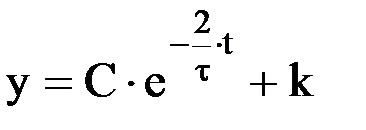Для определения значения постоянной С воспользуемся тем обстоятельством, что y(0) = 0. Следовательно, y(0) = C + k = 0 и C = – k. Таким образом, окончательно имеем

.

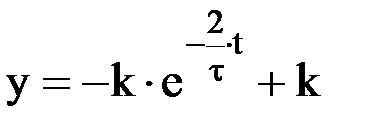Это уравнение представляет собой уравнение апериоди­чес­кого сходящегося процесса.

В случае n = m = 2 порядок изложения аналитической реализации модели аналогичен. Таким образом, имеем

,

.

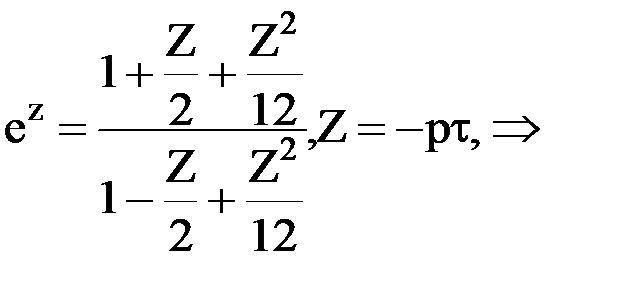
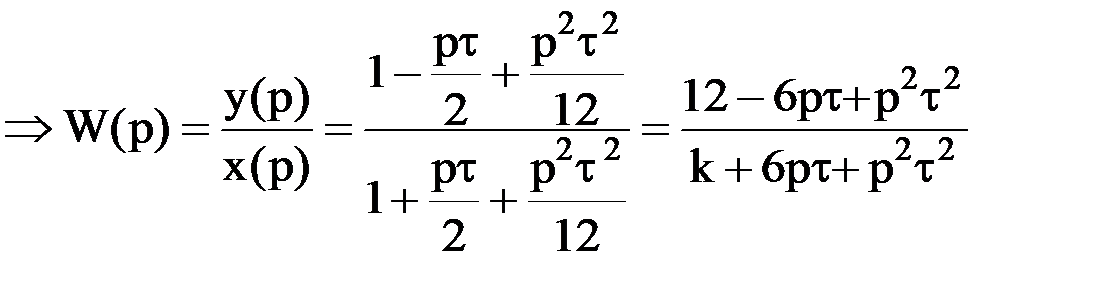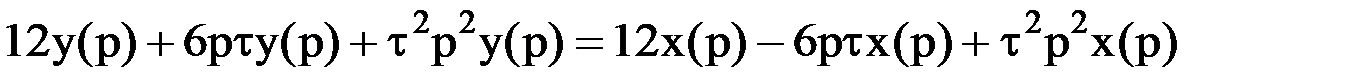Полагаем, что 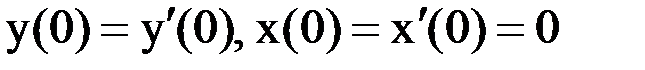. Переходя к ори­гиналам, имеем:

.

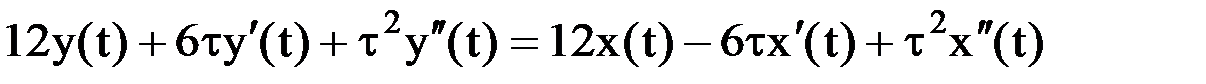Т.к. x(t) = Сonst = k, то

.

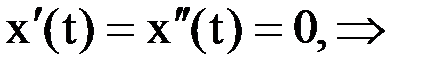
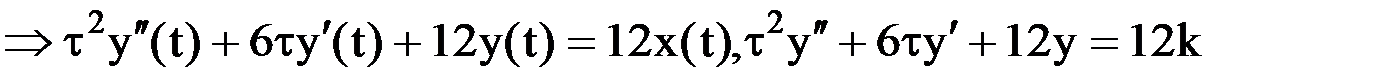Характеристическое уравнение имеет вид:

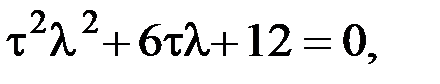
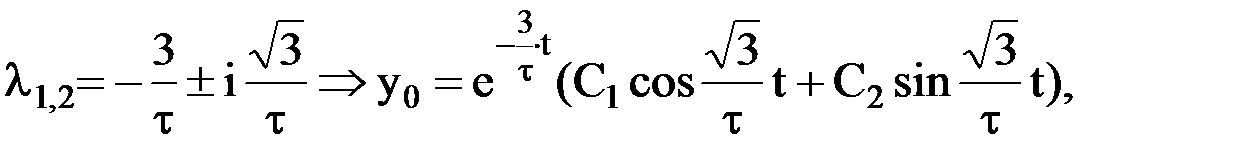
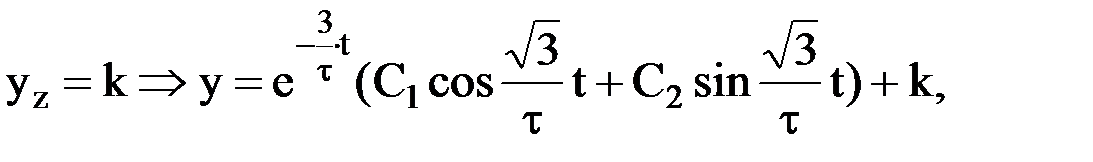
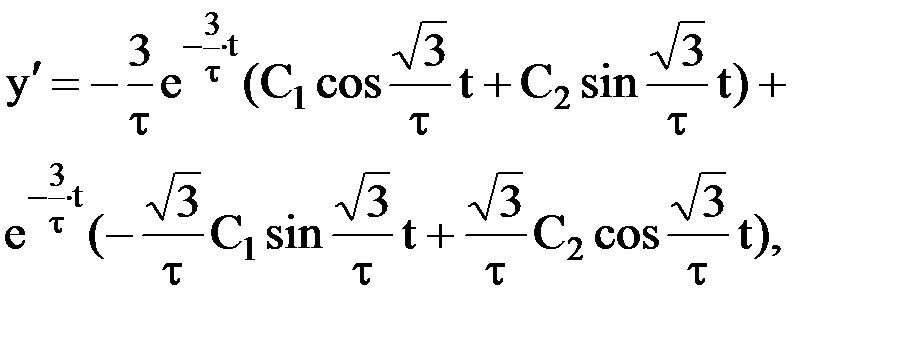
т.к. 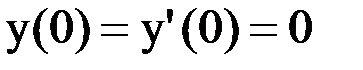, то имеем систему:

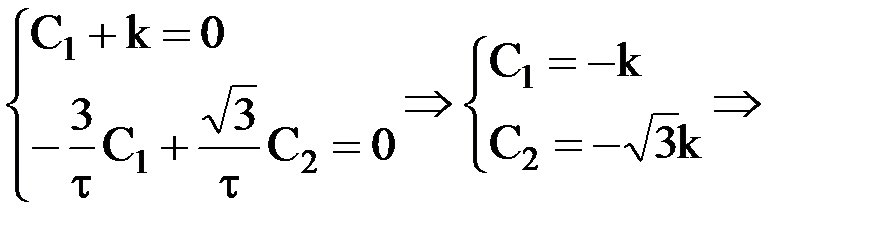
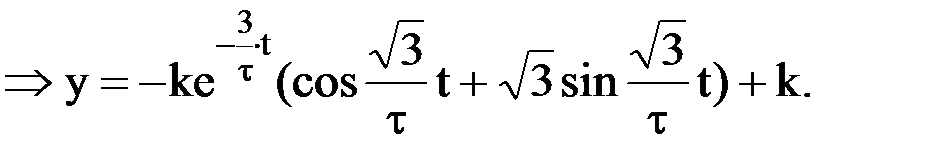
Полученное уравнение представляет собой уравнение периодического сходящегося процесса.

Соответствующие семейства кривых, отражающие влияние параметров на форму решения, представлены в графическом приложении 3.

Практически в реальных физических системах возможна реализация условий функционирования, соответствующих неотрицательным значениям параметров математической модели. Таким образом, на математическую модель накладываются естественные ограничения:

1. функция может являться периодической сходящейся;

2. функция может являться апериодической сходящейся.

Задание на лабораторную работу

Создать математическую модель линейного динамического элемента с запаздыванием с исполь­зо­ва­нием компьютера.

Исследовать поведение модели при различных значениях параметров A₀, A₁, A₂, t — см. выражение (31). Сравнить результаты компьютерного моделирования с результатами, полученными при теоре­ти­чес­ком решении задачи.

В отчете необходимо пред­ставить графики для двух случаев, соответствующих неотрицательным значениям пара­мет­ров модели — периодически и апери­оди­чески сходящегося решения:

1. соответствующего решения — y(t);

2. фазовой траектории решения на фазовой плоскости Oyy’.

Дата добавления: 2014-11-28