Симплексні методи в хімії

.................

Метод крутого сходження

Одержане за допомогою повного факторного експерименту рівняння регресії використовують не тільки для побудови математичної моделі хіміко-технологічного процесу, але і для його оптимізації. Оптимізацією процесу називають цілеспрямований пошук найкращих, у певному розумінні, умов його проведення.

Величина, що характеризує рівень оптимізації, називається критерієм оптимальності або цільовою функцією. Якість хіміко-технологічного процесу, як правило, виражається не однією, а декількома величинами – показниками. Бажано, щоб усі показники одночасно досягали своїх найкращих значень, але як правило, це неможливо.

Для здійснення оптимізації, необхідно володіти певними ресурсами. Наприклад, для збільшення виходу цільового продукту хімічної реакції ми повинні мати можливість варіювати в певних межах значеннями таких величин, як температура реакційної суміші, початкова концентрація реагентів та інші. Оптимізація здійснюється в умовах обмежень на ресурси оптимізації, деякі початкові та кінцеві параметри процесу.

Задача оптимізації формулюється у вигляді: Задано критерій оптимальності...

Y₁ = f (x₁, x₂,..., x _n)

та обмеження на інші кінцеві параметри...

m₂ <= Y₂ <= M₂

m₃ <= Y₃ <= M₃ m – нижня границя

............... M – верхня границя

m _k <= Y _k <= M _k

Задано обмеження на ресурси оптимізації:

x_1mіn <= x₁ <= x_1max

x_2mіn <= x₂ <= x_2max

x _{n mіn} <= x _n <= x _{n max}

Необхідно знайти такі значення ресурсів оптимізації (х₁^*, х₂^*,..., х_n ^*), при яких критерій оптимальності досягає свого екстремального значення.

Д.Бокс та К.Уілсон запропонували використовувати для оптимізації результати повного факторного експерименту.

Серед усіх функцій відгуку, що описують об’єкт оптимізації, вибирається одна з найбільш вагомих та приймають її в якості критерію оптимальності Y₁. Після цього накладаються обмеження на інші функції відгуку та фактори. Один з найбільш впливаючих факторів приймається за базовий і розраховують для нього добуток відповідного коефіцієнта регресії (метод повного факторного експерименту) на крок варіювання. Наприклад, для першого фактору цей добуток має вигляд b₁ ´ Dx₁. Після цього для базового фактору обирається крок (інтервал) варіювання Dх₁^*, з яким буде здійснюватись оптимізація. З метою більш точного знаходження координат оптимізації, приймають, що Dх₁^* £ Dх₁. Тоді розраховується відношення:

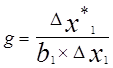(7.5.1)

Для всіх інших факторів крок варіювання при оптимізації розраховується за формулою:

(7.5.2)

Рух до оптимуму починають з центру плану, що був використаний для одержання рівняння регресії. Значення факторів х₁,х₂,...,х_n на кожному етапі оптимізації знаходять шляхом додавання Dх_і^* до відповідних попередніх значень. Тому оптимізацію за методом Бокса та Уілсона називають методом крутого сходження.

Особливості даного методу:

1) Рух з центру плану починається у бік найбільш швидко зростаючого критерію оптимальності. Це відбувається завдяки тому, що інтервали оптимізації Dх_і^* пропорційні коефіцієнтам регресії b_і.

2) Якщо здійснюється пошук мінімуму критерію оптимальності, то нові значення факторів х₁, х₂, …, х_n розраховуються шляхом віднімання Dх_і^*

3) Рух до екстремуму закінчується при виконанні наступних вимог:

а) значення факторів або функцій відгуку вийшли за межі накладених обмежень;

б) досягнуто критерій оптимальності.

4) Під час крутого сходження на поверхні відгуку спочатку знаходять локальний екстремум Y₁ у напрямку руху (рис.7.5.1). Якщо існує декілька екстремумів функцій відгуку необхідно навколо даного екстремуму здійснити новий факторний експеримент та реалізувати пошук нового оптимуму методом крутого сходження.

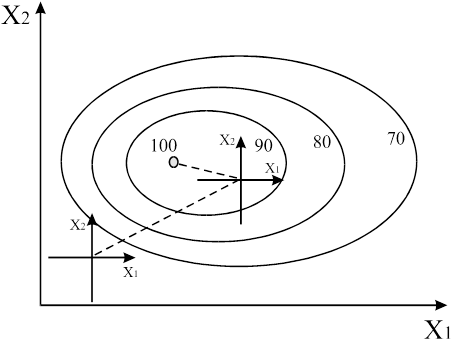
Рис.7.5.1.Оптимізація методом крутого сходження

Для оптимізації хіміко-технологічних процесів широко використовується симплексний метод. Симплексом називають правильний багатогранник з n+1 вершинами, де n - число впливаючих факторів. При кількості факторів, що дорівнює двом, симплекс являє собою правильний трикутник (рис.7.6.1).

Рис.7.6.1.Оптимізація симплексним методом

Початкова серія дослідів відповідає вершинам вихідного симплексу (т.1,2,3). Порівнюючи між собою результати дослідів в даних точках, знаходимо серед них “найгірший” з точки зору обраного критерію оптимальності. Нехай, самим “невдалим” є дослід в т.1. Даний дослід ми вилучаємо з симплексу, замість нього вводимо дослід в т.4, що розташований симетрично до т.1 відносно протилежної сторони трикутника. Далі процедуру порівняння нового симплексу проводимо знову, вилучаючи “невдалий” дослід і замінюючи його новими. Так ми одержуємо нові симплекси, що описують залежність між впливаючими факторами та функціями відгуку. Якщо досягнуто екстремум критерію оптимальності, подальше проходження симплексу закінчується. Це визначає, що новий крок повертає дослідника в попередню точку факторного простору (т.8 і т.10).

Необхідно відмітити, що симплексний метод є локальним методом пошуку екстремуму. Це означає, що в разі існування в факторному просторі, що розглядається, декількох екстремумів критерію оптимальності, даний метод дозволяє знайти той з них, що розташований ближче до точки вихідного симплексу. Тому, якщо існує декілька екстремумів, оптимізацію необхідно здійснювати з нової точки факторного простору з наступним порівнянням знайдених критеріїв оптимальності до вимог проведення хіміко-технологічного процесу.

У процесі оптимізації необхідно враховувати ті обмеження, що накладаються на впливаючі фактори та функції відгуку. При використанні симплексного методу дублювання дослідів є необов’язковим. Похибка в окремому досліді може тільки уповільнити процес оптимізації.

Сипмлексний метод широко використовується при вивченні властивостей сумішей, що залежать від концентрації компонентів суміші. В даному випадку факторний простір являє собою правильний симплекс.

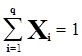(7.6.1)

з q – вершинами в (q-1)-вимірному просторі (де X_і - відносний вміст і -го компоненту суміші). Прикладом такої задачі є визначення залежності температур кристалізації сплавів трикомпонентних систем від складу. При цьому припускається, що досліджувана властивість (Тпл.) є неперервною функцією аргументу та може бути з певною точністю задана поліномом ступеня від q – змінних.

Поліном ступеня n від q змінних в загальному випадку має Сⁿq+n коефіцієнтів, але в нашій задачі змінні Х_і пов’язані між собою співвідношенням SХ_і=1, тому ми одержуємо поліном ступеня n від q-1 змінних, що відповідає кількості коефіцієнтів Сⁿq+n-1. Коефіцієнти поліному являють собою лінійну комбінацію значень, що спостерігаються у вузлах симплексної ґратки, та розраховуються за результатами дослідів. Кількість коефіцієнтів поліному відповідає кількості точок симплексної ґратки. Деякі {q,n} – ґратки наведені на рис.7.6.2.

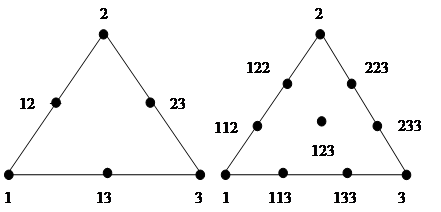
Рис.7.6.2.Симплексні ґратки:

а) {3,2}– квадратична гратка, б) {3,3}– кубічна гратка

Розглянемо більш детально метод математичного планування на симплексі з використанням {3,3}–гратки. В даному випадку, крім експериментальних значень температур топлення чистих компонентів та двох сплавів в кожній бінарній системі, ми повинні мати значення температури топлення потрійного сплаву, що розташований в центрі симплексного трикутника (рис.7.6.2.б.). Матриця планування для {3,3}–кубічної ґратки наведена в таблиці, де “відгук” - значення температур топлення відповідних сплавів.

Поліном, що описує кубічну гратку має вигляд:

Y=b₁X₁+b₂X₂+b₃X₃+b₁₂X₁X₂+b₂₃X₂X₃+b₁₃X₁X₃+q₁₂X₁X₂(X₁-X₂)+

+q₂₃X₂X₃(X₂-X₃)+q ₁₃X₁X₃(X₁-X₃)+b₁₂₃X₁X₂X₃ (7.6.2)

Таблиця 7.6.1.Матриця планування.

№	план	відгук	№	план	відгук
x1	x2	x3	x1	x2	x3
				y1			1/3	2/3	y233
				y2		2/3	1/3		y112
				y3		2/3		1/3	y113
	1/3	2/3		y122			2/3	1/3	y223
	1/3		2/3	y133		1/3	1/3	1/3	y123

Коефіцієнти поліному розраховуються за формулами:

b₁=Y₁, b₂=Y₂, b₃=Y₃,

b₁₂=9/4*(Y₁₁₂+Y₁₂₂-Y₁-Y₂) аналогічно розраховують b₁₃ та b₂₃,

q₁₂=9/4 * (3 * Y₁₁₂-3 * Y ₁₂₂-Y₁+Y₂), аналогічно розраховують q₁₃ та q₂₃,

b₁₂₃=27*Y₁₂₃-27/4*(Y₁₁₂+Y₁₂₂+Y₂₂₃+Y₂₃₃+Y₁₁₃+Y₁₃₃)+9/2*(Y₁+Y₂+Y₃)

Поліном із розрахованими коефіцієнтами використовується для визначення залежності: Y=f(X). Для цього необхідно підставити значення впливаючих факторів Х₁, Х₂, Х₃ до рівняння регресії.

Шляхом нанесення відповідних значень функції відгуку на факторний простір та з’єднанням між собою точок з однаковими значеннями функції відгуку, будується проекція поверхні відгуку на факторній площині за допомогою ліній постійного рівня.

Дата добавления: 2014-11-29