Використання матричних методів в хімії

Метою даної теми є огляд матричних методів, що використовуються при обробці кінетичних даних та при моделюванні кінетики хімічних реакцій.

Вихідним пунктом для більшості кінетичних досліджень - є складання схем можливого перебігу реакцій. При невеликому числі задіяних у ній компонентів даний процес не викликає труднощів. Із зростанням числа елементарних стадій зростають і труднощі при їх складанні. Настає момент, коли необхідно дати відповідь на питання – чи можливо крім наявних елементарних стадій знайти інші, що відповідають сумарній стехіометрії реакції. Тому задача дослідження полягає у вивченні всіх можливих елементарних стадій, що відповідають певним наборам ідентифікованих компонентів.

Перше обмеження, яке необхідно виконати – закон Ломоносова-Лавуазьє (закон збереження маси). Фактично, це є вимога розв’язати систему лінійних рівнянь. Для коректного складання системи лінійних рівнянь, що описують хімічну реакцію, необхідно представити систему у вигляді матричного добутку:

[ A ] ´ [ S ] = 0 (7.8.1)

У прямокутній матриці [A] кожний рядок описує атом, а кожний стовпчик – молекулу. У векторному стовпчику матриці [S] число елементів дорівнює числу стовпчиків у матриці [A] і кожний елемент являє собою невідомий стехіометричний коефіцієнт відповідної молекули в рівнянні, що описує сумарне перетворення. Умовно рахують, що дані елементи додатні для продуктів реакції та від’ємні – для реагуючих речовин. В подальшому матрицю [A] будемо називати стехіометричною.

Наприклад, якщо в реакційній суміші встановлено наявність таких речовин як HІ, Cl₂, HCl, І₂, то можливі елементарні реакції між ними будуть представлені матрицею [A]:

атом	число відповідних атомів у молекулі
	HІ	Cl2	HCl	І2
H
Cl
І

а вектор-стовпчик матриці [S]:

(7.8.2,3)

де G_і – відповідні стехіометричні коефіцієнти, які необхідно знайти (G₁ – для HІ, G₂ – Cl₂, G₃ – HCl, G₄ – І₂).

Для визначення [S] у відповідності до рівняння (7.8.1) необхідно перемножити матриці [A] і [S], та прирівняти елементи одержаного вектор-стовпчика до нуля:

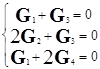(7.8.4)

У системі трьох рівнянь з чотирма невідомими для пошуку рішення одна заміна повинна бути обрана довільно. Нехай G₄ = 1. Тоді розрахунки системи (7.8.4) дають результат: G₁ = –2, G₂ = –1, G₃ = 2, що описує реакцію:

2HІ + Cl₂ = 2HCl + І₂

Необхідно відмітити, що встановлюючи коефіцієнт G₄ додатнім, ми приписуємо речовину І₂ до продуктів реакції. Для знаходження інших наборів G, що узгоджується з ідентифікованими компонентами, необхідно помножити попередній набір G на додатне або від’ємне число.

Особливу увагу приділяють випадкам, коли всі розраховані значення G дорівнюють нулю. Це відповідає системі, в якій ідентифіковані компоненти не відповідають сумарній стехіометрії реакції. Перевіримо дане припущення.

Досліджуємо систему, що складається з компонентів: (NH₄)₂CO₃, NH₃, H₂O, CO.

Стехіометрична матриця має вигляд:

атом	(NH4)2CO3	NH3	H2O	CO
N
H
C
O

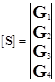(7.8.5,6)

переходить у систему

(7.8.7)

Нехай G₄ = 1, тоді G₁ = –1, G₃ = 2, але неможливо розрахувати значення G₂ (не виконується рівняння 2 системи). Єдиним розв’язком даної системи є випадок, коли всі значення G дорівнюють нулю.

При заміні в системі компоненту СО на СО₂ (вносяться відповідні зміни до стехіометричної матриці) одержуємо систему рівнянь:

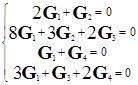(7.8.8)

при G₄ = 1 отримуємо G₁ = –1, G₃ = 1, G₂ = 2, що відповідає реакції:

(NH₄)₂CO₃ Þ 2NH₃ + H₂O + CO₂

Розрахувавши ступінь вільності ми можемо встановити напрямок перебігу реакцій. Ступінь вільності знаходять як різницю між числом задіяних молекул (кількість невідомих) та числом атомів (кількість рівнянь). В першому випадку ступінь вільності дорівнює одиниці, що вказує на можливість перебігу двох паралельних реакцій: прямої та зворотної, в другому – нулю (можлива лише пряма реакція розкладу карбонату амонію). Дана різниця легко знаходиться, якщо рівняння незалежні, що не завжди має місце в дійсності. Тому при розрахунках ступеня вільності особливу увагу звертають на визначення числа незалежних рівнянь у схемі реакції. Комз дав рішення даної проблеми, що базується на перевірці рангу реакційної матриці. Використання алгоритму Гаусса-Жордана дає можливість одночасно знайти кількість ступіней вільності та можливі елементарні акти, що сполучені з системою експериментально ідентифікованих компонентів.

Метод Гаусса-Жордана є загальним методом обертання квадратичних матриць або рішення систем лінійних рівнянь. На першому етапі перевіряється рівність нулю коефіцієнтів кожного рівняння. Нехай, і -те рівняння на даний момент перевірено. Помножимо його член на константу та одержане еквівалентне рівняння додамо до залишившихся n-1 рівнянь. Константу підбираємо таким чином, щоб в усіх даних n-1 рівняннях і -тий член скоротився. Таким чином, ми одержуємо нову еквівалентну систему рівнянь, в кожному з яких ми маємо одне невідоме та сталий член. Для мінімізації похибок, порядок в системі рівнянь зручно модифікувати таким чином, щоб рівняння з найбільшим із перевірених коефіцієнтів стало першим у системі.

Для пояснення розглянемо систему з набором ідентифікованих компонентів: HІ,Cl₂, HCl, І₂. При G₄ = 1 система (7.8.4) має вигляд:

(7.8.9), що пов’язана з матрицею:

(7.8.10)

Помножимо рівняння (7.8.10.1) на –1, додамо одержані рівняння до (7.8.10.3), що дасть нову, еквівалентну попередній систему:

(7.8.11)

Наступний етап полягає у використанні аналогічної послідовності операцій до (7.8.11.2), але в нашому випадку в цьому нема потреби, так як елементи другого стовпчика рівнянь (7.8.11.1) та (7.8.11.3) нульові. Додаємо вираз (7.8.11.3) до рівнянь (7.8.11.1) та (7.8.11.2) так, щоб скоротити член третього стовпчика. Внаслідок даних перетворень одержуємо матрицю:

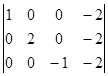(7.8.12), що трансформується в (7.8.12)

Розв’язком системи (7.8.12) буде: G₁= –2, G₂ = –1, G₃ = 2.

Метод Гаусса-Жордана також розповсюджується на матричні рівняння, що містять однакову або більшу кількість рядків, ніж стовпчиків. В такому випадку розрахунок дає матрицю, що містить таку ж або меншу ніж стовпчиків кількість ненульових рядків. Ранг матриці (або кількість незалежних рівнянь) дорівнює різниці між числом стовпчиків та рядків (числом молекул і числом атомів, з яких складаються дані молекули).

Більшість випадків використання методу Гаусса-Жордана приводить до реакційної матриці, що трансформується в матрицю з меншою кількістю ненульових рядків, ніж стовпчиків. Дана ситуація можна проілюструвати на прикладі фотохлорування метану. В експериментальній суміші наявні компоненти: CH₄, Cl₂, HCl, CH₃Cl, CH₂Cl₂, CHCl₃, CCl₄, які описується реакційною матрицею:

	CH4	Cl2	HCl	CH3Cl	CH2Cl2	CHCl3	CCl4
C
H
Cl

Дана реакційна матриця трансформується в систему:

(7.8.13)

Дана система має (7-4) ступенів вільності, тобто описується 4-ма видами незалежних рівнянь. Дані рівняння називаються базисними. Люба реакція, що пов'язана з початковою системою, може бути одержана за допомогою лінійної комбінації базисних реакцій. Для кожного типу систем базис знаходять таким шляхом. Останні чотири стовпчика реакційної матриці, що одержується в результаті використання алгоритму Гаусса-Жордана, послідовно піддають перевірці. В розглядаємому стовпчику для компонента, що описується, встановлюють коефіцієнт G = –1, а для трьох інших компонентів (три з чотирьох вихідних) дані коефіцієнти встановлюють рівними нулю. Тоді коефіцієнти перших трьох вихідних компонентів просто вилучають з стовпчика, що пов’язаний із досліджуваним продуктом.

CH₄ + Cl₂ Þ CH₃Cl + HCl можливі

CH₄ + 2Cl₂ Þ CH₂Cl₂ + 2HCl базисні

CH₄ + 3Cl₂ Þ CHCl₃ + 3HCl реакції

CH₄ + 4Cl₂ Þ CCl₄ + 4HCl

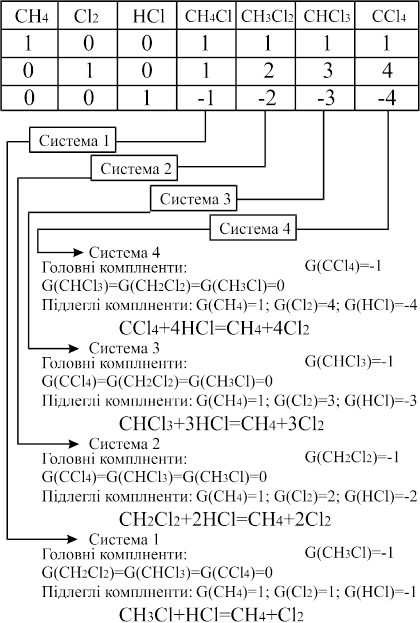
Компоненти, що описуються останніми чотирма стовпчиками називаються головними, так як встановлення G= –1 для одного з них робить їх вихідними. Інші три величини є похідними від величини, що встановлена головним коефіцієнтом. Тому їх називають підлеглими.

Дата добавления: 2014-11-29