Рассмотрим примеры

Число степеней свободы точки

Независимые возможные перемещения.

Для каждой точки и механической системы в целом с учётом наложенных на них связей можно указать определённое количество таких независимых между собой возможных перемещений, что всякое другое будет получаться в виде некоторой комбинации эти независимых. Количеством независимых между собой возможных перемещений точки (тела, системы) определяется число их степеней свободы.

Материальная точка, вынужденная двигаться вдоль некоторой линии, имеет одну степень свободы (рис. 1.2).

Рис. 1.2

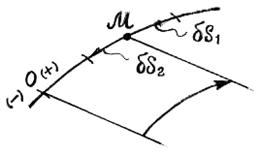Из данного положения 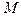она может получить возможное перемещение 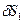или 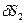в одну или другую сторону. Очевидно, что они не могут произойти одновременно и только одно из них можно считать независимым. Положение самой точки на линии
можно определить, например, дуговой координатой 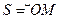(см. раздел ''Кинематика'', естественный способ задания движения точки). Если точка должна оставаться на некоторой поверхности, то она имеет 2 степени свободы.

Действительно, эта связь допускает два независимых возможных перемещения (например, взаимно перпендикулярных 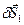и 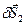, по касательным к поверхности) (рис. 1.3).

Рис. 1.3

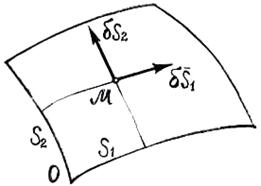Положение самой точки 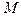на поверхности можно определить двумя криволинейными координатам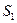и и 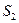. Именно так определяется положение корабля в открытом море (географи-ческими координатами – широтой и долготой местности), или декартовыми координатам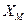и и 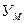определяется положение точки на плоскости и т.п.

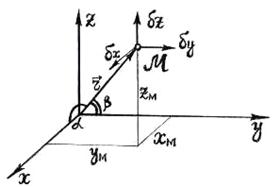
Свободная материальная точка имеет 3 степени свободы (рис. 1.4) – независимые возможные перемещения её могут происходить в трёх взаимно перпендикулярных направлениях 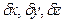. А любое другое возможное перемещение найдётся как линейная комбинация этих независимых возможных перемещений:

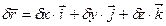. (1.1)

Рис. 1.4

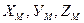Положение самой точки в пространстве тоже определяется тремя координатами . Вместо них можно использовать другие параметры. Например, ими могут быть длина вектора 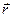(т.е. 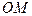) и углы 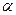и 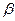, образуемые вектором 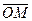с осям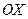и и 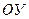и т.п.

Из приведенных примеров видно, что наложение на точку каждой удерживающей геометрической связи уменьшает на единицу число независимых возможных перемещений её и соответственно на единицу же уменьшается число степеней свободы (рис. 1.3). Например, линия в геометрии рассматривается как пересечение двух поверхностей. Поэтому,
если точка должна оставаться на некоторой линии, то число наложенных на неё геометрических связей равно двум. И точка на линии имеет 3 – 2 = 1 степень свободы (рис. 1.2). Неподвижная точка – это пересечение трёх поверхностей. И степень подвижности такой точки, конечно, равна нулю.

Дата добавления: 2014-11-29