
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матричный метод расчета УЗМИ
|
|
|
|
Рассмотрим волновод поперечного сечения длиной l (рис. 4). Общее решение уравнения (8) для этого случая - уравнения (9) в виде
 , (16)
, (16)
в силу второго из соотношений (1), амплитуда осевых условий n (z)
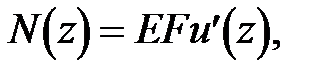
и с учетом (16а)
 , (17)
, (17)
Пусть амплитуда продольного смещения при z =0 равна 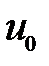 , а амплитуда осевого усилия
, а амплитуда осевого усилия 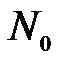 . Тогда соотношение (16а) и (17) примут вид
. Тогда соотношение (16а) и (17) примут вид
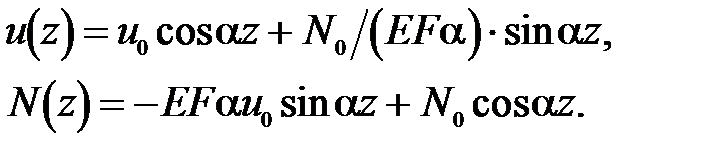
Значения смещения и усилия на правом торце волновода:
 (18)
(18)
 Рис. 4
Рис. 4
|
Используя векторные обозначения, уравнение (18) можно записать в более компактной форме  , где
, где  ; - вектора-столбца: A - матрица
; - вектора-столбца: A - матрица  вида:
вида:

которую принято называть матрицей перехода. Для участков УЗМИ с экспоненциальными, катеноидальными и коническими переходами (7) решение  также может быть выражено через
также может быть выражено через  , а элементы матрицы перехода A будут равны
, а элементы матрицы перехода A будут равны

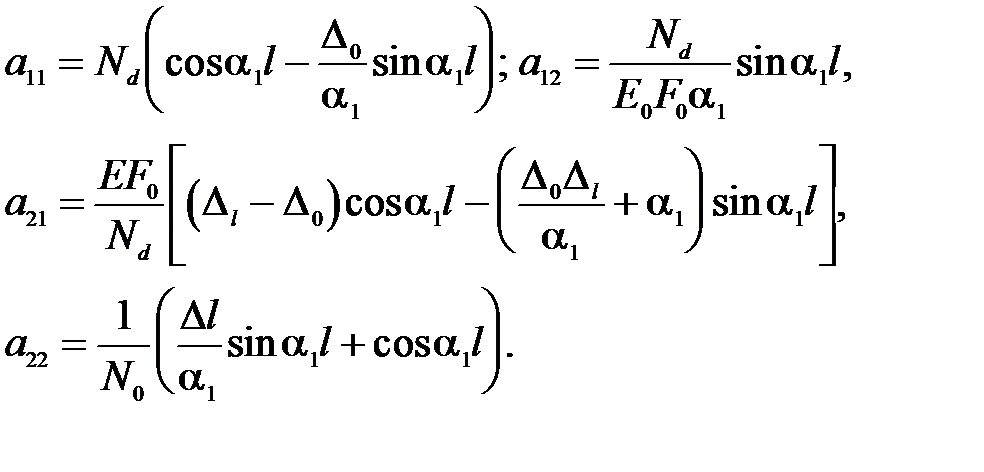 (20)
(20)
где 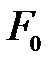 - площадь поперечного сечения в начале участка
- площадь поперечного сечения в начале участка
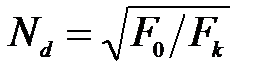 ;
; 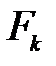 - площадь поперечного сечения в конце участка.
- площадь поперечного сечения в конце участка.
Для волновода с экспоненциальными переходами 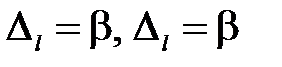 ;
;
Для волноводов с катеноидальными переходами 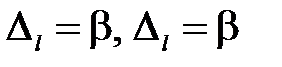
Для волноводов с коническими переходами 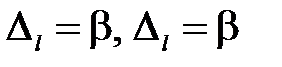 ,.
,.
Для крутых переходов (рупоров), когда 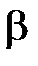 или
или  больше
больше 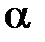 , все тригонометрические функции в матрице перехода следует заменить на соответствующие гиперболические (это не касается конических рупоров).
, все тригонометрические функции в матрице перехода следует заменить на соответствующие гиперболические (это не касается конических рупоров).
Допустим, УЗМИ состоит из участков, в пределах каждого из которых закон изменения площади поперечного сечения таков, что может быть аппроксимирован одной их функций (7), и для каждого из участков введена локальная система координат  , начало каждой из которых совпадает с левым (см. рис 4) краем соответствующего i-ого участка. Вектор решения при
, начало каждой из которых совпадает с левым (см. рис 4) краем соответствующего i-ого участка. Вектор решения при 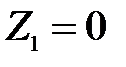 имеет вид:
имеет вид: 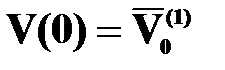 . Тогда решение в конце первого участка будет выглядеть так:
. Тогда решение в конце первого участка будет выглядеть так:  , но силу условий сплошности и равновесия вектор решения в начале следующего участка
, но силу условий сплошности и равновесия вектор решения в начале следующего участка  совпадает с
совпадает с  . Решение в конце второго участка:
. Решение в конце второго участка: 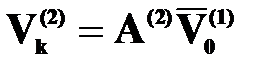 , но
, но  , тогда
, тогда 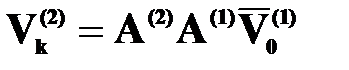 ,.
,.
Решение в конце i-ого участка:
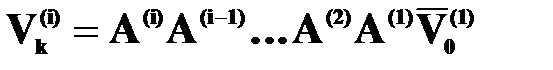
. Решение в конце n -ого участка: (т.е. при  , где
, где  - длина i-ого участка, l - полная длина ультразвуковой колебательной системы) имеет вид
- длина i-ого участка, l - полная длина ультразвуковой колебательной системы) имеет вид
 (21)
(21)
где 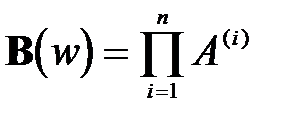 .
.
Собственные частоты (резонансные длины) УЗМИ находятся из  решения системы (21), при этом должны выполняться граничные условия на правом и левом краях интервала [0, 1].
решения системы (21), при этом должны выполняться граничные условия на правом и левом краях интервала [0, 1].
Рассмотрим различные варианты граничных условий:
1) левый и правый края свободны (N =0), тогда


в этом случае имеем следующее частотное уравнение:
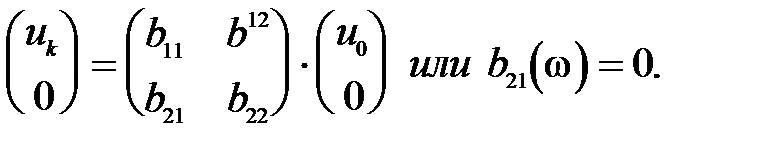
2) Левый край свободен (N =0), правый заделан (u =0), тогда 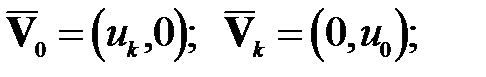
в этом случае имеем следующее частотное уравнение:

Решение частотных уравнений вида 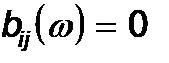 может быть найдено известными способами, например методом половинного или пропорционального деления, методом хорд, касательных, Ньютона-Зейделя и других.
может быть найдено известными способами, например методом половинного или пропорционального деления, методом хорд, касательных, Ньютона-Зейделя и других.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 602; Нарушение авторских прав?; Мы поможем в написании вашей работы!