Выбор материалов для элементов УЗМИ

Проблема правильного подбора материала для элементов УЗМИ имеет существенное значение, так как от решения этой про­блемы зависит прочность и надежность инструмента, его коррозион­ная стойкость, износостойкость, габариты, масса, КПД УЗМИ.

Проанализируем работу однополуволнового волновода постоян­ного поперечного сечения с целью выяснения влияния свойств мате­риала волновода на возможность получения максимальной ампли­туды колебаний. Для этого рассмотрим однополуволновой волновод постоянного поперечного сечения со свободными торцами, стацио­нарные колебания которого описываются уравнением (8), а решение имеет вид 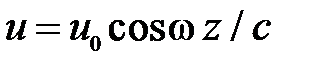, где 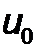- амплитуда колебаний торцов волно­вода, а продольная деформация волновода

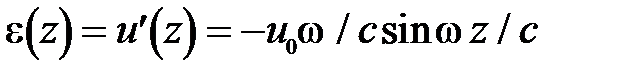
максимальна при и равна

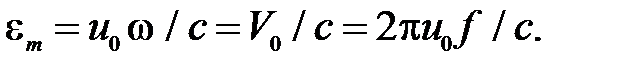(39)

Но, считая материал линейно-упругим вплоть до некоторого на­пряжения, равного допускаемого по усталостной прочности 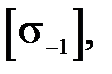, максимальная деформация не должна превышать величины 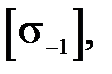. Приравнивая эту величину правой части равенства (39), используя также известное соотношение между c и E, получим выражение для амплитудного значения перемещения

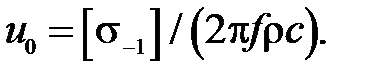(40)

Из этого выражения следует, что максимально возможное сме­щение торцов волновода зависит от механических свойств материала и резонансной частоты колебаний, и лишь материалы с высокой уста­лостной прочностью и низким волновым сопротивлением позволяют развивать большие амплитуды смещения.

Зависимость (40) можно несколько видоизменить, учитывая, что резонансная частота волновода постоянного поперечного сечения со свободными торцами определяется как 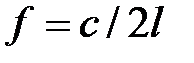, тогда

.

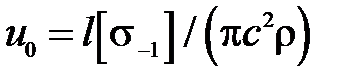Откуда следует, что наиболее сильно на амплитуду смещений влияет скорость звука c, однако с уменьшением последней также уменьшается и резонансная частота волновода (при l =cons t).

Соотношения, подобные (40), были получены в более общем виде и для волноводов переменного поперечного сечения Э.Эйснером и Х.Кренделлом, которое вместо соотношения (40) для амплитудного значения перемещения использовали аналогичное соотношение для максимальной колебательной скорости в волноводе с целью исклю­чения из рассмотрения частоты колебаний. Нетрудно предположить, что характер зависимости (40) для волновода постоянного попереч­ного сечения останется прежним и для волноводов переменного се­чения, так Эйснером и другими исследователями получена зависи­мость

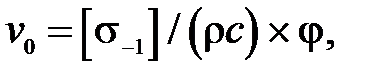(41)

где - безразмерный коэффициент, зависящий от закона изме­нения поперечного сечения (для волновода постоянного поперечного сечения 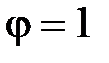, см. соотношение (40)) и получивший название фактора формы. Этот результат интересен тем, что максимальная возможная колебательная скорость в волноводе представляется в виде двух со­множителей, первый из которых зависит только из свойств мате­риала, а второй - только от формы волновода. Таким образом, подбор наилучшего материала можно производить вне зависимости от того, какой концентратор из этого материала будет выполнен, а материалы необходимо подбирать с максимально возможным значением . Анализируя механические свойства существующих материалов по ко­эффициенту , можно с уверенностью утверждать, что широко доступных материалов со свойствами, лучшими, чем у титановых сплавов, пока нет.

Большое значение имеет выбор материала, который бы обеспе­чивал минимальный вес УЗМИ продольных колебаний. Поскольку такой инструмент можно рассматривать как набор волноводов-кон­центраторов продольных колебаний, условие минимума веса G каж­дого из волноводов можно представить в виде

(42)

Это условие нельзя свести лишь к условию минимума плотности , потому что уменьшение плотности при постоянстве остальных па­раметров и свойств приводит к возрастанию скорости звука (т.е. ) и увеличению длины волновода, так как при фиксирован­ной резонансной частоте f длина волновода пропорциональна скоро­сти звука. Если F=F (z), то

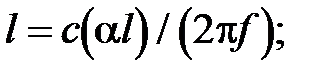
где 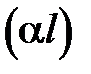- корень частотного уравнения для основного резонанса. Тогда условие (42) можно преобразовать к виду

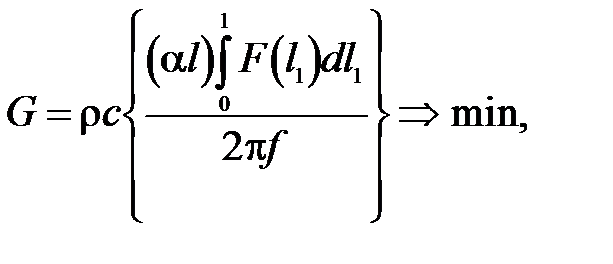
причем выражение, стоящее в фигурных скобках, зависит только от конфигурации волновода и частоты основного резонанса f. Из по­следнего выражения следует, что необходимо подбирать материал с наименьшим волновым сопротивлением 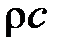для того, чтобы получить волновод, а следовательно, и УЗМИ наименьшего веса.

Что касается такого фактора, как потери на внутренне рассея­ние механической энергии и связанный с этим фактором КПД всего УЗМИ, то при выборе материала необходимо стремиться к тому, чтобы рассеиваемая мощность была минимальной, т.е. как следует из выражения (38), следует выбирать материал с минимальным .

Дата добавления: 2014-11-29