Определение собственных частот изгибных колебаний элементов УЗМИ

В связи с расширением номенклатуры медицинского ультразвукового инструментария все чаще возникают проблемы рас­чета рабочих окончаний, совершающих изгибные колебания. Уравне­ние, описывающее малые изгибные (поперечные) колебания прямо­линейного изотропного стержня, имеет вид [1]

(23)

где 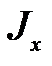- геометрический момент инерции поперечного сече­ния;

y(z,t) - поперечное смещение z -го сечения в момент времени t;

q(z,t) - внешняя нагрузка;

При решении задачи на собственные значения q(z,t)=0, а реше­ние уравнения (23) обычно ищется в виде

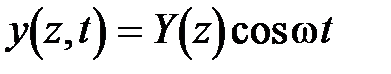(24)

После подстановки (24) в (23) и преобразований получим

(25)

Краевые условия. В простейших случаях, когда край бруса сво­боден или жестко закреплен, или шарнирно оперт, краевые условия выражаются следующими соотношениями:

а) коней стержня жестко закреплен; на таком конце прогиб y (z, t) (или его амплитудное значение Y (z)) и угол поворота 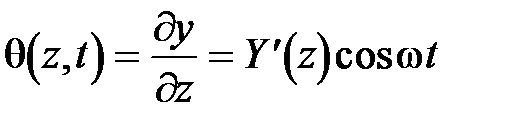равны нулю, т.е.

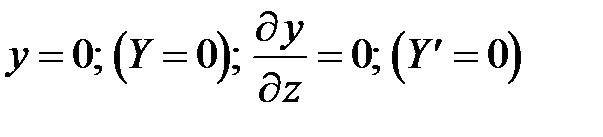; (26)

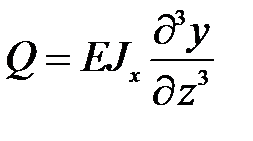б) конец стержня свободен; на таком конце изгибающий момент и поперечная сила равны нулю, следова­тельно

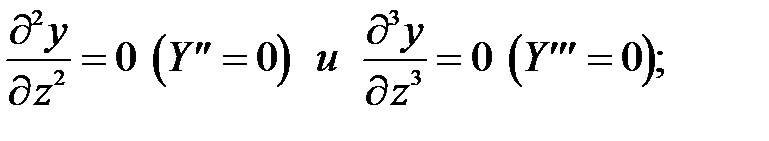(27)

в) конец стержня свободно оперт

(28)

Если заданы свойства материала бруса (элемента УЗМИ), т.е. плотность 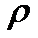, модуль Юнга E, а также размеры этого элемента, т.е. - длина элемента, то задача определения собственной частоты r сводится к численному решению дифференциального уравнения (25) для заданных граничных условий (26)-(28) и итера­ционному (например, методом бисекции) нахождению собственной частоты 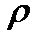. Рассмотрим, как это выполняется в случае , для которого существует аналитическое реше­ние уравнения (25).

Элемент УЗМИ постоянного поперечного сечения. Так как , то уравнение (25) после деления на примет вид

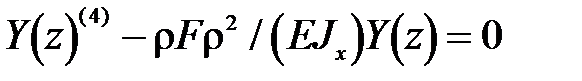(29)

или

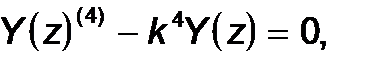(29)

где 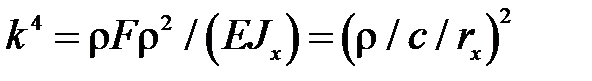- радиус инерции поперечного се­чения.

Характеристическое уравнение для дифференциального уравне­ния (29а):

.

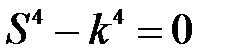Решение этого уравнения: .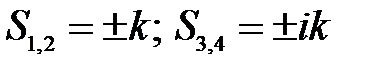

Тогда общее решение дифференциального уравнения (29а) будет выглядеть так:

Решение может быть также выражено через функции Крылова [1]

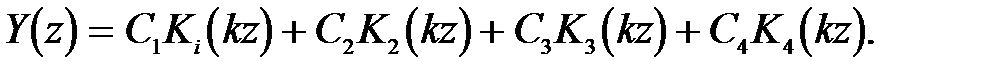(30)

Функции Крылова имеют вид:

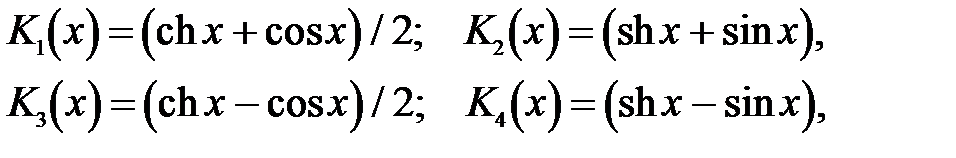
и обладают рядом преимуществ. Так, при аргументе x =0

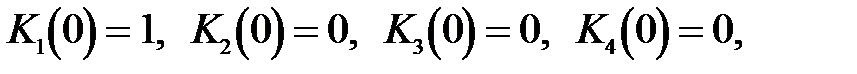(31)

а дифференцирование функций Крылова осуществляется про­стой круговой заменой индексов,

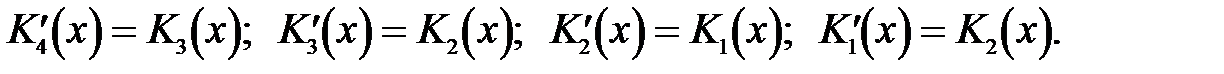
Найдем выражение для углов поворота 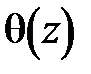, изгибающих мо­ментов M (z), поперечной силы Q (z), учитывая, что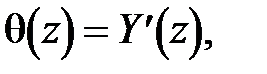 , тогда

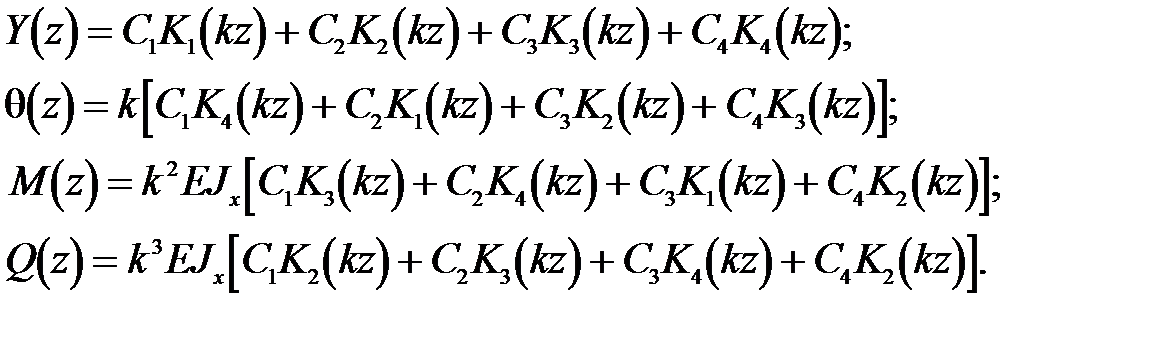(32)

Будем считать, что при z =0 заданы значения перемещений 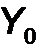, углов поворота 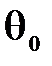, момента и поперечной силы 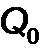. Выразим со­ответствующие значения констант 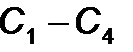через 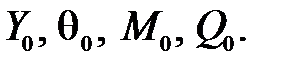Соотно­шения (32) при z =0, с учетом свойств функций Крылова (31), примут вид

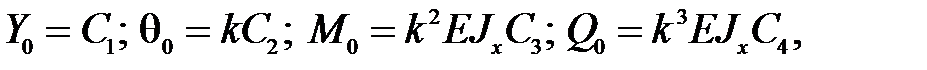
тогда

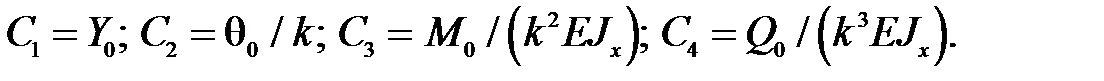
Подставляя полученные для 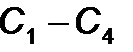соотношения в уравнения (32) и переходя к матричной форме записи, имеем

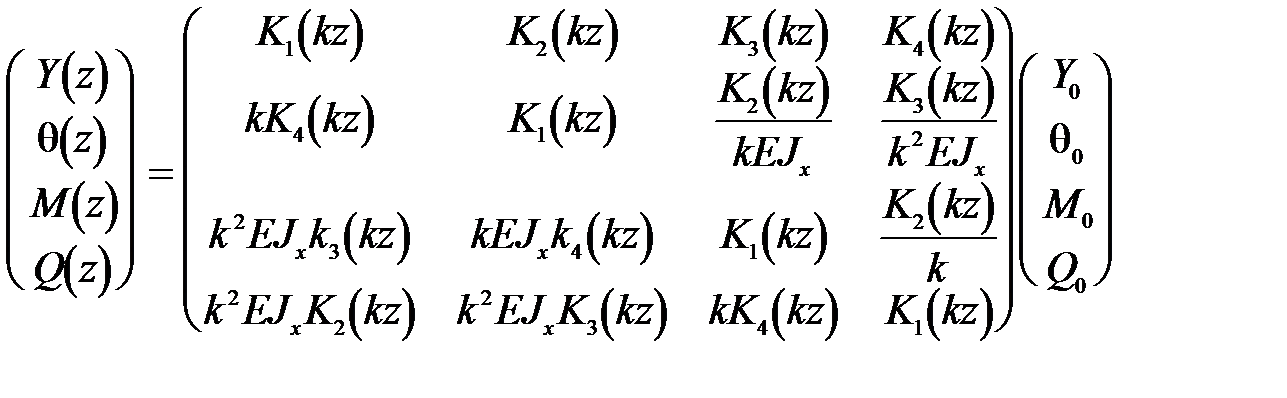(33)

или

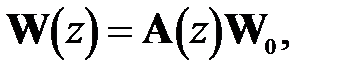(33а)

где 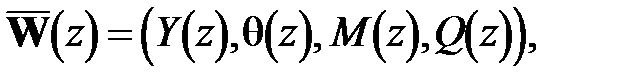- вектор-столбец;

A - соответствующая матрица коэффициентов;

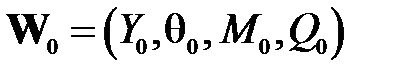- вектор-столбец.

Допустим, необходимо определить собственную частоту изгиб­ных колебаний стоматологического инструмента, изображенного на рис.8а. Расчетная схема инструмента изображена на рис.8б. Изложен­ный выше (см.§ 2 гл.2) матричный метод расчета УЗМИ можно также использовать и при изгибных колебаниях УЗМИ. Тогда при z =0 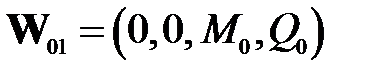, а при . Далее можно записать, что

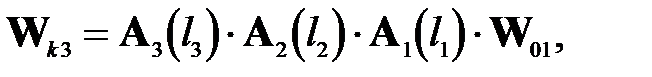(34)
где 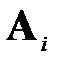- матрица перехода для i-ого участка (i =1,2,3).

Причем

или

где

или

Причем полученная система уравнений имеет нетривиальное решение в случае, когда

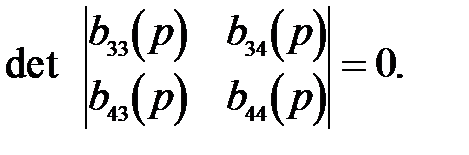(35)

Рис. 8

Применяя, на­пример, метод би­секции, задавая ин­тервал 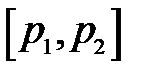, нахо­дят значение p, при котором уравнение (35) обращается в ноль. Это значение и есть резонансная частота изгибных ко­лебаний инстру­мента. При этом следует помнить, что корней уравнения (35) беско­нечное множество, и учитывать его при задании интервала поиска корней в итерационных методах.

Дата добавления: 2014-11-29