
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пьезоэлектрические преобразователи. Электроакустические преобразователи медицинского назначения
|
|
|
|
Электроакустические преобразователи медицинского назначения
В качестве электроакустических преобразователей на частотах от 20 до 80 кГц используются как магнитострикционные, так и пьезокерамические преобразователи. Однако на частотах свыше 80 кГц обычно применяются лишь пьезопреобразователи, так как потери в пьезопреобразователях на высоких частотах значительно меньше потерь в магнитострикционных преобразователях.
В пьезоэлектрических преобразователях в качестве активного элемента, осуществляющего электроакустическое преобразование энергии, применяются элементы из пьезоэлектрических материалов. Для приема ультразвуковых волн используется прямой эффект - возникновение электрической индукции D в пьезоэлементе в результате действия механических напряжений  , а для возбуждения - обратный пьезоэффект - возникновение деформаций при создании в пьезоэлементе переменного электрического поля.
, а для возбуждения - обратный пьезоэффект - возникновение деформаций при создании в пьезоэлементе переменного электрического поля.
Связь между деформацией  , электрическим полем
, электрическим полем 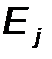 , упругим напряжением
, упругим напряжением 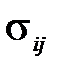 и электрической индукцией
и электрической индукцией  (где i, j, k =1, 2, 3) при малых величинах воздействия описывается линейными уравнениями прямого
(где i, j, k =1, 2, 3) при малых величинах воздействия описывается линейными уравнениями прямого
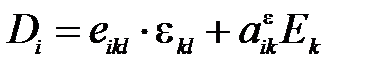 (43)
(43)
и обратного пьезоэффектов [6]
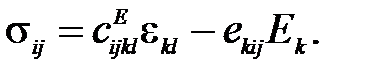 (44)
(44)
Для гексагонального класса симметрии  , к которому можно отнести широко распространенные пьезокерамики, полученные поляризацией внешним электрическим полем, уравнения (43) и (44) упрощаются и принимают вид:
, к которому можно отнести широко распространенные пьезокерамики, полученные поляризацией внешним электрическим полем, уравнения (43) и (44) упрощаются и принимают вид:
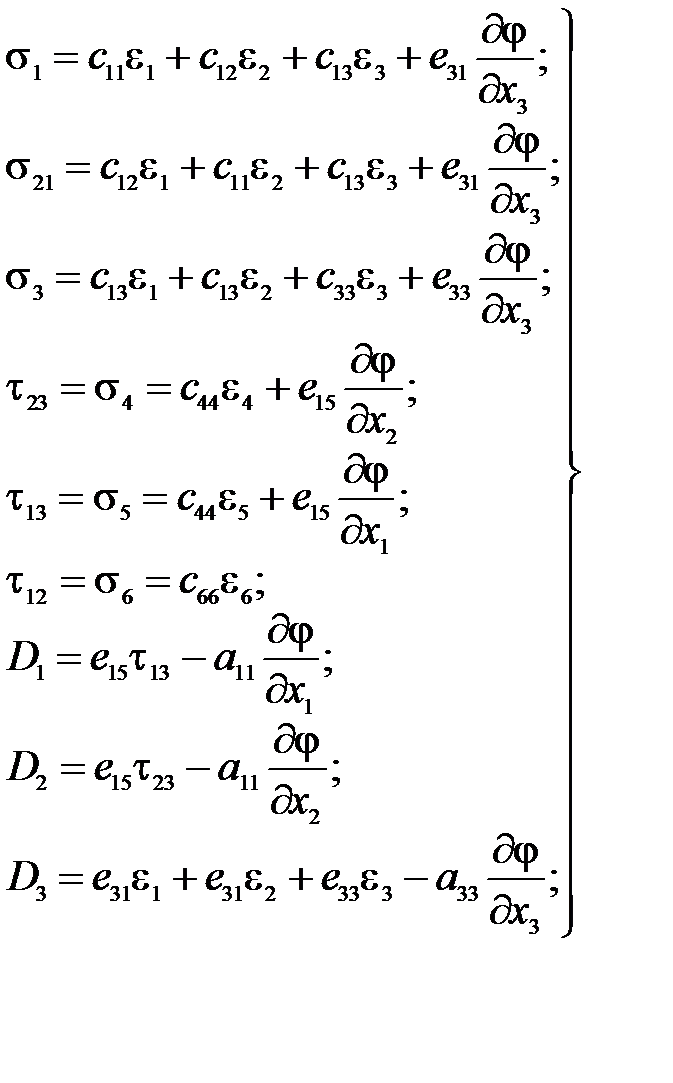
|
(45)
где 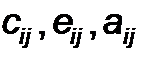 - соответственно упругие, пьезоэлектрические и диэлектрические постоянные; переход от тензорной записи к матричной осуществляем заменой индексов i, j или k, l на p или q по правилу
- соответственно упругие, пьезоэлектрические и диэлектрические постоянные; переход от тензорной записи к матричной осуществляем заменой индексов i, j или k, l на p или q по правилу  а также
а также  при i=j и
при i=j и 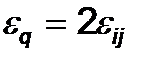 при
при  . Кроме того, в (45) учтено, что напряженность электрического поля
. Кроме того, в (45) учтено, что напряженность электрического поля  связана с потенциалом соотношением
связана с потенциалом соотношением 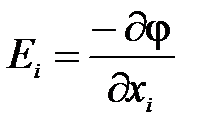 , i =1,2,3, а ось
, i =1,2,3, а ось 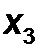 совпадает с направлением поляризации.
совпадает с направлением поляризации.
Для одномерного случая, когда пьезоэлемент совершает колебания лишь в направлении оси поляризации 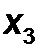 и вектор электрического поля E параллелен этой оси, уравнения (45) упрощаются:
и вектор электрического поля E параллелен этой оси, уравнения (45) упрощаются:
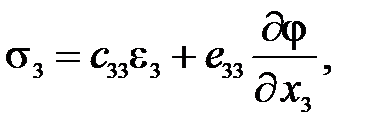 (46)
(46)
 (46а)
(46а)
Из-за большого различия скоростей распространения электромагнитных и упругих волн связью между ними пренебрежем, тогда процесс возбуждения и распространения межденных упругих волн описывается в соответствии с принципом д'Аламбера первым уравнением системы (1) в форме
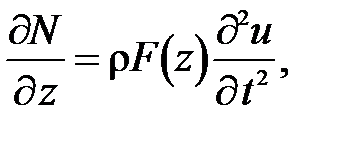 (47)
(47)
а соотношение для N в силу уравнения (46) примет вид
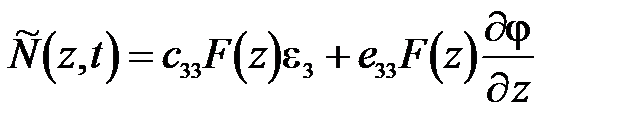
(здесь и далее ось  обозначена z), то так как
обозначена z), то так как 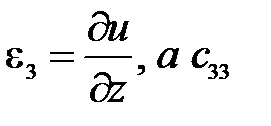 - это модуль Юнга E, то
- это модуль Юнга E, то
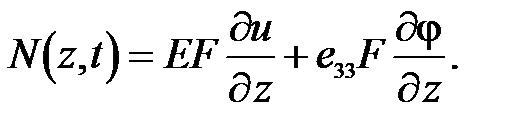
Однако в большинстве случаев УЗМИ работает в резонансном режиме, при котором вся подводимая к УЗМИ энергия идет на излучение в нагрузку и на рассеяние в элементах УЗМИ. Учтем потери на механический гистерезис, тогда последнее выражение для N примет вид
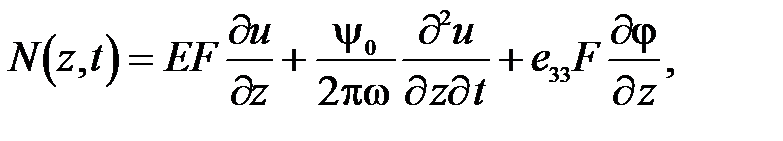 (48)
(48)
где 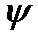 - коэффициент поглощения в материале УЗМИ.
- коэффициент поглощения в материале УЗМИ.
При стационарных продольных колебаниях, обусловленных разностью потенциалов 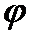 , меняющейся гармонически, т.е.
, меняющейся гармонически, т.е.
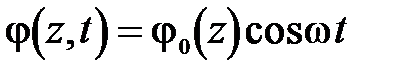 (49)
(49)
или
 , (50)
, (50)
где 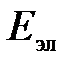 - напряженность электрического поля.
- напряженность электрического поля.
Решение системы уравнений (47), (48) ищется в виде
 (51)
(51)
тогда уравнение (47) после подстановки в него соотношений (51) распадается на два:
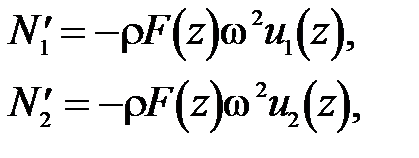 (52)
(52)
а уравнение (48) после приравнивания слагаемых при cos и sin с учетом (50) и того что  , распадается также на два:
, распадается также на два:
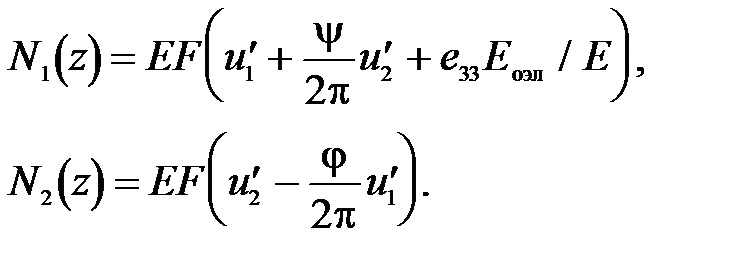
Разрешая полученные выражения для  относительно
относительно 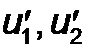 , имеем
, имеем
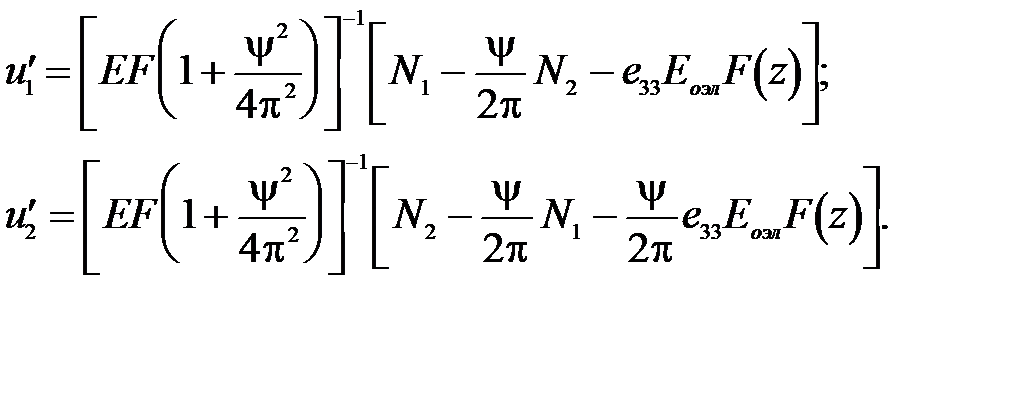 (53)
(53)
Таким образом, система обыкновенных дифференциальных уравнений (52), (53) четвертого порядка, разрешенная относительно первых производных, может быть легко решена на ЭВМ с применением численных методов (например, методом Адамса, Рунге-Кутта, Хемминга и т.п.).
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!