Система управления с подчиненным регулированием координат

В теории автоматического управления для замкнутого контура с передаточной функцией

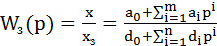(7.12)

известны различные критерии оптимизации с помощью настройки регулятора, последовательно включенного с объектом управления. Широкое применение для ЭП нашел динамический оптимум, так называемый Betragsoptimum – модульный оптимум (МО), означающий следующее: замкнутый контур динамически оптимален, если он одина-ково передает на выход разночастотные входные сигналы на возможно большем интервале частот, т. е. на этом интервале модуль АЧХ замкнутого контура

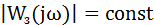. (7.13)

Условие (7.13) выполняется, если при ω>0 возможно большее число производных модуля АЧХ по частоте стремится к нулю, т.е.

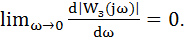(7.14)

Условию (7.14) соответствуют определенные соотношения коэф-фициентов числителя и знаменателя передаточной функции замкнутого контура (7.12):

,

,

……………………………………………………….

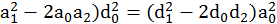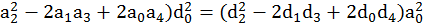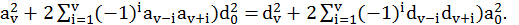(7.15)

Teopетически МО может дать бесконечно большую полосу пропускания контура (ω_п.п→∞), если в выражении (7.12) т = п и а_i = d_i (рис. 7.3). Однако практически это недостижимо из-за ограниченных возможностей реальных регуляторов и конечной полосы пропускания датчиков.

Рис. 7.3. Амплитудно-частотные характеристики (1 – 3) замкнутого контура регулирования

Поэтому модульный оптимум называют также техническим оптимумом. Оптимизация на максимум полосы пропускания является также оптимиза-циией по быстродействию. Чем шире полоса пропускания, тем меньше время переходного процесса контура.

В инерционном контуре регулирования можно выделить две части – с большой инерционностью и с весьма малой инерционностью, обусловлен-ной фильтрами датчиков и преобразователей сигналов и характеризуемой не-которой малой постоянной времени Т_μ.

Передаточная функция объекта управления с учетом Т_μ имеет вид

, (7.16)

где k_О.У – коэффициент усиления объекта управления. Принимая для регу-лятора передаточную функцию вида

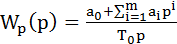, (7.17)

получаем для замкнутого контура передаточную функцию

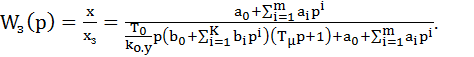(7.18)

Коэффициенты регулятора а₀, а_i, T₀ находятся из уравнений (7.15). Очевидно, что условие (7.13) будет выполнено максимально, если при-нять т = к, а₀ = b₀, а_i = b_i. Тогда при b₀ = 1

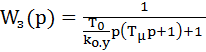. (7.19)

Согласно первому уравнению (7.15);

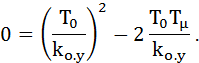
Откуда

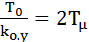, (7.20)

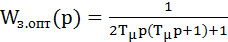. (7.21)

Таким образом, регулятор, компенсирующий инерционности объекта управления, имеющий интегральную составляющую с постоянной време-ни T₀=2k_о.уT_μ, обеспечивает максимальное быстродействие замкнутому кон-туру.

Для объекта управления в виде колебательного звена второго порядка потребуется пропорционально – интегрально - дифференциальный (ПИД) регулятор; для апериодического звена первого порядка – пропорциональ-но-интегральный (ПИ) регулятор; для интегрального звена – пропорцио-нальный (П) регулятор.

Если для интегрального объекта управления с передаточной функ-цией

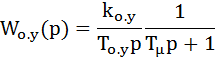
использовать вместо П-регулятора ПИ-регулятор с передаточной функ-цией

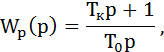
то передаточная функция замкнутого контура получит вид

(7.22)

Подключив к входу контура апериодическое звено с передаточной функцией

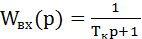, (7.15)

то настройка полученной системы на МО по уравнениям даст значения параметров ПИ-регулятора:

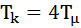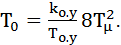; (7.23)

Данная настройка носит название симметричный оптимум (СО). Этому названию соответствует симметричная относительно точки час-тоты среза ω_ср=1/2T_μ ЛАЧХ оптимизированного разомкнутой контура с передаточной функцией

(7.24)

Если сложный объект управления представляет собой последова-тельность перечисленных выше инерционных звеньев W₁, W₂,, W₃,…,W_n, соединенных друг с другом контролируемыми координатами х₁ х₂, х₃,..., x_n, то для каждой координаты может быть составлен замкнутый контур с регулятором, настроенным на описанный выше динамический оптимум типа МО или СО (рис. 7.4) и настройка регуляторов W_pl, W_p2, W_p3,..., W_pn производится в направлении от внутреннего контура с номером 1 к контуру с номером п, являющемуся внешним контуром (рис.7.4,п=3). В состав объекта управления контура с номером i входит настроенный оптимально замкнутый контур с номером i - 1. Если для каждого следующего после первого контура компен-сировать регулятором W_pi инерционности звена W_i пренебрегая его ма-лой постоянной времени Т_μ, то получим

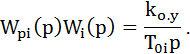
Рис. 7.4. Структурная схема системы подчиненного регулирования координат ЭП

Настраивая интегральную составляющую регулятора по условию МО (7.20)

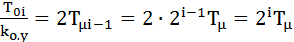, (7.25)

получаем передаточную функцию замкнутого i-го контура

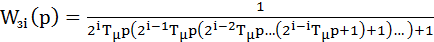, (7.26)

где Т_μ – малая постоянная времени, отнесенная к первому контуру.

Чем больше контуров в системе подчиненного регулирования, тем меньше быстродействие внешнего контура. По сравнению с однокон-турной системой быстро действие n-контурной системы уменьшается в 2^n-1 раз.

Трехконтурная система описывается дифференциальным уравне-нием четвертого порядка. Однако настройка на модульный оптимум поз-воляет без большой погрешности оценивать динамические показатели системы по уравнению второго порядка

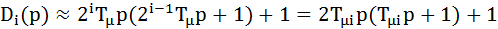. (7.27)

Данному уравнению соответствует переходная функция h(t)=x(t)\x₃, т.е. переходный процесс отработки замкнутым контуром скачка зада-ющего сигнала х₃. Эта функция имеет вид

. (7.28)

Перерегулирование составляет 4,3 %, а время переходного процесса ~ 4Т_μ.

Дата добавления: 2014-11-29