Гипербола. Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых от двух заданных точек этой же плоскости

Эллипс

УРАВНЕНИЯМИ

Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых от двух заданных точек этой же плоскости, называемых фокусами, есть постоянное число 2 а, большее, чем фокальное расстояние 2 с между фокусами .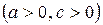

Пусть М – произвольная точка эллипса, а F ₁ и F ₂ – его фокусы. Отрезки MF ₁ и MF ₂ так же, как и длины этих отрезков r ₁ и r ₂ называются фокальными радиусами точки М эллипса. В силу данного определения эллипса

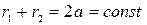. (5.3)

Выразим фокальные радиусы r ₁ и r ₂ через координаты точек М, F ₁ и F ₂. Для этого введем на плоскости декартову прямоугольную систему координат хОу, принимая середину отрезка F ₁ F ₂ за начало координат, а за ось Ох – прямую F ₁ F ₂, ориентированную от точки F ₁ к точке F ₂ (рис.3.8). В выбранной системе координат фокус F ₁ будет иметь координаты – с, 0, а фокус F ₂ – координаты с, 0. Обозначая координаты точки М через х и у, будем иметь

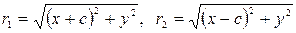
и соотношение (5.3) принимает вид

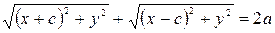. (5.4)

На первый взгляд, не ясно, относится ли уравнение (5.4) к уравнениям кривых второго порядка типа (5.2). Выполним некоторые преобразования уравнения (5.4), в частности, избавимся от иррациональности. Перенесем первый радикал в правую часть и обе части полученного уравнения возведем в квадрат:

.

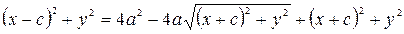Отсюда после преобразований находим

.

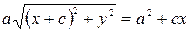Возводя обе части этого уравнения в квадрат, получим

,

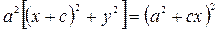или

.

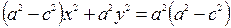Так как по условию 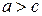, то 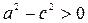. Обозначая 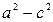через 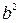и учитывая, что 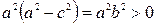, получим

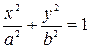. (5.5)

Мы доказали, что координаты любой точки М (х, у) эллипса удовлетворяют уравнению (5.5), следовательно, и уравнению кривой второго порядка (5.2) при условии, что

.

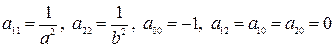Однако уравнение (5.5) еще нельзя назвать уравнением эллипса, так как не доказано обратное утверждение, а именно: если числа х и у удовлетворяют уравнению (5.5) и при этом 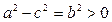, то точка М с координатами х и у удовлетворяет соотношению (5.4), т.е. лежит на эллипсе.

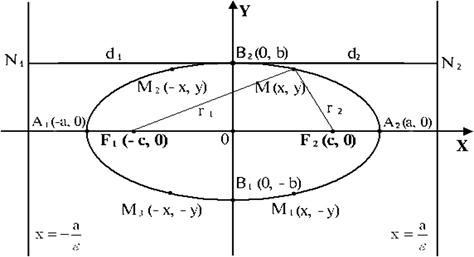
Рис. 3.8

Докажем это. Пусть координаты точки М (х, у) удовлетворяют уравнению (5.5). Тогда из уравнения (5.5) находим .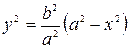

Определим фокальные радиусы точки М (х, у)

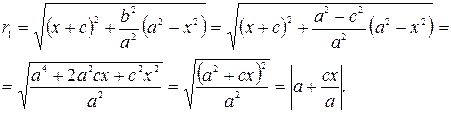
Аналогично можно получить значение r ₂:

.

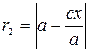Так как

,

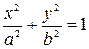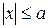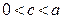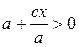то , а так как , то и 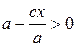, следовательно,

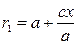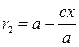, , (5.6)

откуда

.

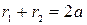Таким образом, уравнение (5.5) является уравнением эллипса и называется каноническим.

Свойства эллипса:

1. Из канонического уравнения эллипса (5.5) следует, что эллипс относится к кривым второго порядка.

2. Из уравнения (5.5) следует, что .

Геометрически это значит, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые 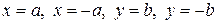, т.е. эллипс есть ограниченная кривая.

3. Так как в каноническое уравнение эллипса координаты х и у входят в четной степени (а именно, во второй), то если на эллипсе лежит точка М (х, у), то на том же эллипсе лежат точки М ₁(х,– у) и М₂ (– х, у), симметричные с точкой М относительно осей Ох и Оу, и точка М₃ (– х,– у), симметричная с точкой М относительно начала координат (рис.3.8). Поэтому оси координат Ох и Оу для эллипса, заданного каноническим уравнением (5.5), являются осями симметрии, а начало координат – центром симметрии.

Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Таким образом, эллипс 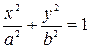имеет четыре вершины: 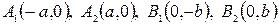(рис.3.8).

Величины 2 а и 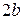называется соответственно большой и малой осями эллипса, а а и 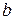– большой и малой полуосями.

Разрешая уравнение эллипса относительно у и беря для него лишь неотрицательное значение

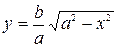(5.7)

и считая, что 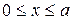, получим точки эллипса (5.5), лежащие в первой четверти. Из уравнения (5.7) следует, что значения у с возрастанием х от нуля до х = а убывают, причем 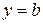при х = 0 и у = 0 при х = а. Добавив к дуге, заданной уравнением (5.7), дуги, ей симметричные относительно осей координат и начала координат, получим замкнутую линию, которая и будет представлять график эллипса в целом.

Итак, эллипс – замкнутая линия, имеющая единственный центр симметрии и только две (если 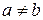) взаимно перпендикулярные оси симметрии.

Кривая, имеющая центр симметрии, называется центральной.

4. Если в уравнении (5.5) 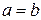, то получим уравнение окружности

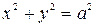(5.8)

с центром в начале координат и радиусом а.

Таким образом, окружность – это эллипс, у которого фокусы совпадают с центром симметрии, т.е. фокальное расстояние 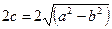равно нулю.

Для характеристики эллипса вводят отношение 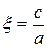, которое называют эксцентриситетом эллипса

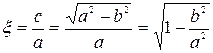. (5.9)

Эксцентриситет характеризует отклонения эллипса от окружности – степень «вытянутости» эллипса. Для окружности 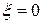. Для эллипса .

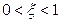Прямые 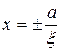называются директрисами (направляющими) эллипса. Поскольку 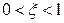, то 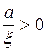и, значит, директрисы эллипса отстоят от его центра дальше, чем вершины (рис.3.8). Окружность (для которой 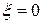) не имеет директрис.

Особенность директрис состоит в том, что отношение фокального радиуса любой точки эллипса к соответствующему расстоянию до директрисы есть величина постоянная, равная эксцентриситету эллипса. Действительно (см. рис.3.8),

.

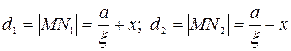Тогда, с учетом (5.6)

, .

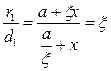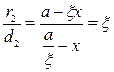Таким образом, .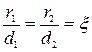

5. В случае 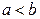большей полуосью будет b и фокусы расположены на оси Оу на расстоянии 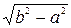от центра эллипса.

6. Как следует из уравнения (5.5), эллипс задан, если заданы его полуоси а и b или а и с. По этим полуосям можно построить эллипс.

Одним из способов построения эллипса является следующий. Берут нерастяжимую нить длиной 2 а; концы нити закрепляют в фокусах F ₁ и F ₂; карандашом натягивают нить и вычерчивают эллипс.

В заключение рассмотрим параметрические и полярные уравнения эллипса.

Параметрическими уравнениями эллипса являются уравнения

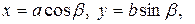(5.10)

где 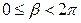. В этом легко убедиться, подставив эти уравнения в каноническое уравнение эллипса (5.5):

.

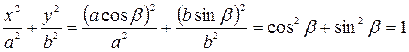Параметр 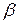называется эксцентрическим углом точки эллипса. Если задана точка М эллипса, то для нахождения 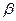надо построить окружность на большей оси эллипса как на диаметре и через точку М провести прямую, параллельную малой оси эллипса. Точка Р пересечения этой прямой с окружностью, лежащая по ту же сторону от большой оси эллипса, что и точка М, называется прообразом точки М (при установлении взаимнооднозначного соответствия между точками окружности и эллипса). Угол от оси Ох до луча ОР и является эксцентрическим углом 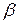, соответствующим взятой точке М на эллипсе (рис.3.9).

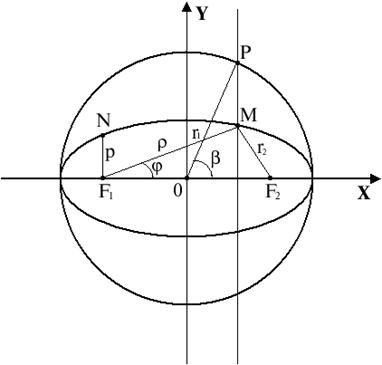
Рис. 3.9

Для установления полярного уравнения введем полярную систему координат так, чтобы ее полюс совпадал с фокусом F ₁, а полярная ось – с лучом F ₁ x (рис.3.9).

Согласно определению эллипса, .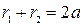

По условию r ₁ =r. Тогда r ₂ =2a – r.

Из треугольника MF ₁ F ₂ по теореме косинусов находим

,

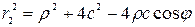откуда

.

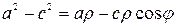Учитывая, что 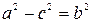, получаем 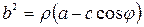. Отсюда

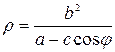, или .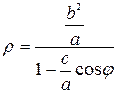

Обозначим 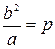. Число р называется фокальным параметром эллипса; оно равно длине перпендикуляра, восстановленного из фокуса к фокальной оси до пересечения с эллипсом, т.е. 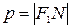(рис.3.9).

Таким образом, уравнение эллипса в полярных координатах имеет вид

,

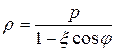где 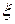и р – соответственно эксцентриситет и фокальный параметр эллипса.

Можно показать, что если за полюс полярной системы координат взять фокус F ₂. а направление полярной оси оставить прежним, то уравнение эллипса в полярных координатах примет вид

.

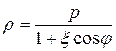Определение. Гиперболой называется геометрическое место точек, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное положительное число 2 а, меньшее, чем расстояние 2 с между фокусами.

Пусть М – произвольная точка гиперболы, а F ₁ и F ₂ – ее фокусы. Отрезки F ₁ M и F ₂ M так же, как и их длины r ₁ и r ₂, называются фокальными радиусами гиперболы. Поэтому

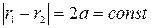. (5.11)

Введем на плоскости прямоугольную систему координат, принимая середину отрезка F ₁ F ₂ за начало координат, а за ось Ох – прямую F ₁ F ₂, ориентированную от точки F ₁ к точке F ₂. В выбранной системе координат фокус F ₁ имеет координаты – с, 0, а фокус F ₂ – координаты с, 0. Обозначая координаты точки М гиперболы через х, у, получим

, ,

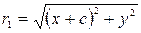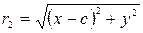и соотношение (5.11) принимает вид

.

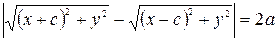Преобразуя это уравнение так же, как и для эллипса (п.1.1), получим уравнение

.

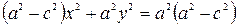Однако теперь 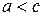. Обозначая разность 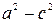через 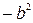: 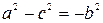или 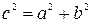, имеем

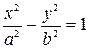. (5.12)

Итак, координаты любой точки гиперболы удовлетворяют уравнению (5.12). Справедливо и обратное утверждение: если координаты точки удовлетворяют этому уравнению, то эта точка лежит на рассматриваемой гиперболе. Доказательство аналогично тому, что было выполнено при выводе уравнения эллипса.

Следовательно, уравнение (5.12) является уравнением гиперболы: оно называется каноническим уравнением гиперболы.

Свойства гиперболы:

1. Гипербола есть кривая второго порядка.

2. Каноническое уравнение гиперболы (5.12) содержит текущие координаты в четных степенях, следовательно, гипербола, как и эллипс, имеет две оси симметрии – оси координат и один центр симметрии – начало координат.

3. Из уравнения (5.12) следует, что 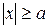, т.е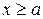. или , или 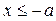. Поэтому гипербола состоит из двух ветвей. Левая ветвь лежит в полуплоскости 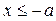, а правая – в полуплоскости 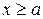. Между прямым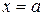и и нет ни одной точки гиперболы.

4. Ось симметрии Оу не пересекает гиперболу, заданную уравнением (5.12), и называется мнимой осью; ось Ох пересекает гиперболу в двух точках: 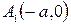и 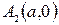. Эта ось называется действительной осью гиперболы. Точки, в которых действительная ось пересекает гиперболу, называется вершинами гиперболы.

Числа а и 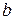в каноническом уравнении (5.12) гиперболы называются соответственно действительной и мнимой полуосями гиперболы.

5. Решая уравнение (5.12) относительно у, беря для него лишь положительное значение

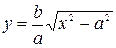(5.13)

и считая 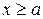, мы получим точки гиперболы, лежащие в первой четверти. Из уравнения (5.13) следует, что с неограниченным возрастанием х от а значения у также неограниченно возрастают. Затем, воспользовавшись тем, что гипербола симметрична относительно осей координат, мы получим точки гиперболы, лежащие в остальных (второй, третьей и четвертой) четвертях (рис.3.10).

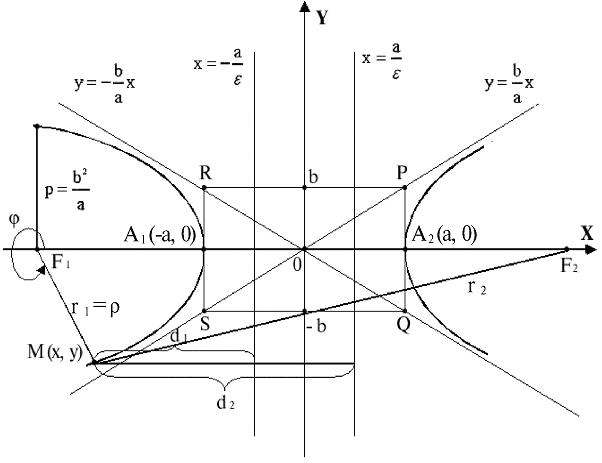
Рис. 3.10

6. Прямые, определяемые уравнениям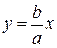и и 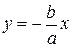, называются асимптотами гиперболы. Асимптота гиперболы – это прямая, обладающая тем свойством, что точка на гиперболе, удаляющаяся от начала координат в бесконечность, неограниченно приближается к ее асимптоте (рис.3.10).

Асимптоты гиперболы совпадают с диагоналями прямоугольника с вершинами 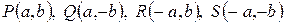(рис.3.10).

Дадим теперь способ построения гиперболы, использующий асимптоты. Строим прямоугольник SRPQ (стороны этого прямоугольника 2 а и 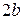); проводим прямые, совпадающие с диагоналями этого прямоугольника, т.е. проводим асимптоты; затем вычерчиваем гиперболу с вершинами в точках А ₁ и А ₂.

7. Отношение расстояния от центра гиперболы до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы:

.

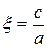Так как для гиперболы 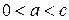, то 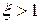и эксцентриситет гиперболы больше единицы.

Две прямые, заданные уравнениям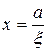и и 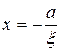, называются директрисами гиперболы.

Так как 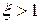, то директрисы гиперболы отстоят от ее центра на расстоянии, меньшем действительной полуоси (рис.3.10). Директрисы гиперболы обладают тем же свойством, что и директрисы эллипса, т.е.

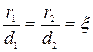(рис.3.10).

В заключение рассмотрим параметрические и полярное уравнения гиперболы.

Перепишем уравнение (5.12) гиперболы в виде

.

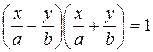Отсюда видно, что

, .

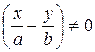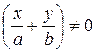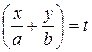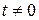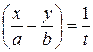Положим , тогда и , следовательно

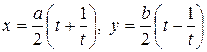. (5.14)

Мы доказали, что координаты любой точки гиперболы могут быть представлены в виде (5.14), где 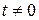. Обратно, при любом 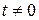точка с координатами (5.14) лежит на гиперболе

,

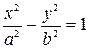в чем легко можно убедиться, подставляя в это уравнение вместо х и у их выражения из формул (5.14). Следовательно, уравнения (5.14) являются параметрическими уравнениями гиперболы.

Для установления полярного уравнения гиперболы введем полярную систему координат так, чтобы ее полюс совпал с фокусом F ₁. а полярная ось – с положительным направлением оси Ох. Координаты любой точки М гиперболы обозначим через ρ и φ, т.е. 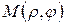(см. рис.3.10).

Запишем уравнение гиперболы в виде 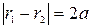, или для правой ветви

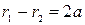, (5.15)

а для левой

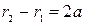. (5.16)

Запишем уравнение (5.16) в полярных координатах. Для любой точки М левой части гиперболы 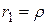. Тогда .

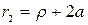По теореме косинусов из треугольника 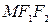(рис.3.10) находим

,

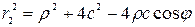или

,

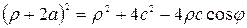откуда

.

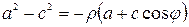Учитывая, что 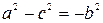, а 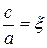, получаем

.

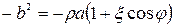Обозначив фокальный параметр гиперболы через 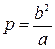(см. рис.3.10), приходим к полярному уравнению левой ветви гиперболы:

.

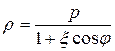Аналогично выводится полярное уравнение правой ветви гиперболы:

.

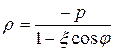Если полюс поместить в правый фокус F ₂, а направление полярной оси сохранить, то полярное уравнение правой ветви гиперболы принимает вид

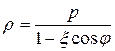, (5.17)

а левой

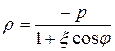. (5.18)

Дата добавления: 2014-11-29