Моделирование оптимального управления уровнем

В ЁМКОСТИ С ПОМОЩЬЮ ПИ-РЕГУЛЯТОРА

В данном разделе рассматривается задача определения оптимальных настроек ПИ-регулятора уровня жидкости в емкости.

На рисунке 1.1 представлен объект управления и принципиальная схема регулирования уровня жидкости в ёмкости.

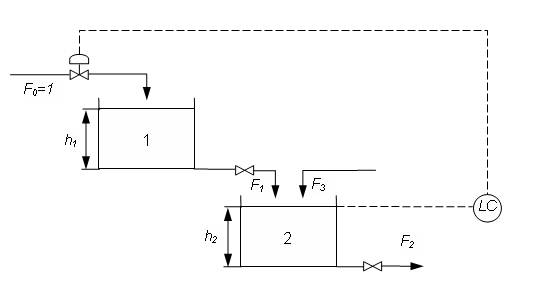
Рисунок 1.1 – Принципиальная схема регулирования уровня жидкости

в ёмкости

Регулирование уровня в емкости осуществляется по принципу отклонения регулируемой величины от заданного значения. Уровень в ёмкости 2 поддерживается на заданном значении регулированием входного потока в ёмкость 1. Эта ёмкость играет роль запаздывания в системе. Задача регулятора заключается в том, чтобы сохранять заданный уровень в ёмкости 2, несмотря на возмущения, которые происходят в потоке F ₃.

Уравнения математического описания при постоянной плотности можно записать в следующем виде:

для ёмкости 1: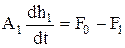

для ёмкости 2: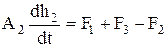

Уравнения расходов через вентили задаются в виде:

, .

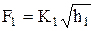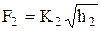Возмущения, которые происходят в потоке F ₃ смоделируем в виде импульсного возмущения,показанного в протоколе решения задачи (см.рисунок 1.2),

Уравнение пропорционально-интегрального регулятора представим в виде:

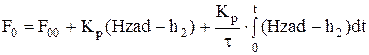
Критерий качества регулирования по отклонению регулируемой величины от заданного значения запишем в следующем виде:

Таблица 1.1 – Спецификация принятых обозначений и их размерность.

Обозначения	Наименование	Размерность
a1,a2	Площади поперечного сечения емкостей	м^2
Fi	Расход соответствующего потока, .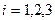
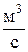
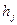
	Уровень жидкости в соответствующей ёмкости,	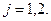м
k1, k2	Коэффициенты, характеризующие пропускную способность вентилей емкостей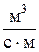
Кр	Пропорциональная составляющая регулятора	-
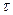
	Время изодрома	с
АМР	Амплитуда	-
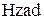
	Заданное значение уровня во второй емкости h2, который нужно поддерживать постоянным	м

Математическое описание процесса регулирования уровня в ёмкости представим в виде системы дифференциальных уравнений:

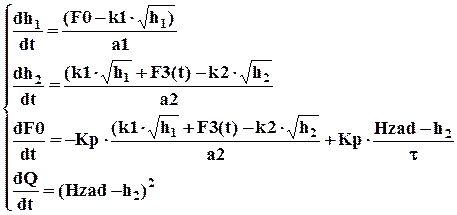
Начальные условия при :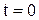

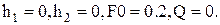
Третье уравнение системы представляет собой уравнение для ПИ- регулятора, записанное в виде дифференциального уравнения.

Постановка задачи. Для исследуемой системы найти такие значения параметров настройки ПИ-регулятора: коэффициент пропорциональности -Kp и время изодрома- 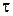,при которых критерий качества регулирования был бы минимальным.

При интегрировании системы дифференциальных уравнений на каждом шаге решения оптимальной задачи воспользуемся методом Эйлера.

В соответствие с этим методом система дифференциальных уравнений сводится к решению системы рекуррентных соотношений:

,

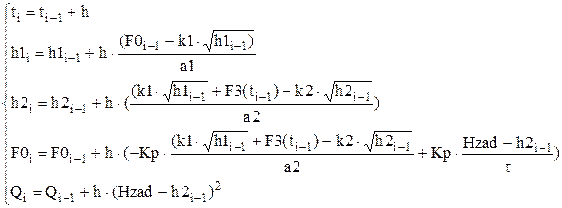где

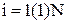,N-число частей разбиения интервала интегрирования.

Для решения оптимальной задачи воспользуемся функцией Minimize в системе компьютерной математики Mathcad.

На следующих рисунках 1.2-1.6 показаны протоколы решения задачи.

Рисунок 1.2-Задание исходных данных

Рисунок 1.3- Программа для вычисления качества регулирования

На рисунке 1.3 представлен фрагмент программы, которая реализует вычисление критерия оптимизации с использованием метода Эйлера.

В ней приняты следующие обозначения:

2.1- Таблица условных обозначений в программе:

Переменная	Предыдущий шаг	Следующий шаг
t	tpr	tsl
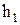
	h1pr	h1sl
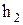
	h2pr	h2sl
F0	F0pr	F0sl
Q	Qpr	Qsl

Интервал времени интегрирования равный 200 с разбит на 10000 частей.

Рисунок 1.4-Решение задачи оптимизации

На рисунке 1.4 представлен фрагмент программы для решения задачи оптимизации с помощью функции Minimize.

На рисунках 1.5 -1.6 представлены результаты проверки найденного оптимального режима и проиллюстрированы полученные результаты при найденных оптимальных настройках регулятора.

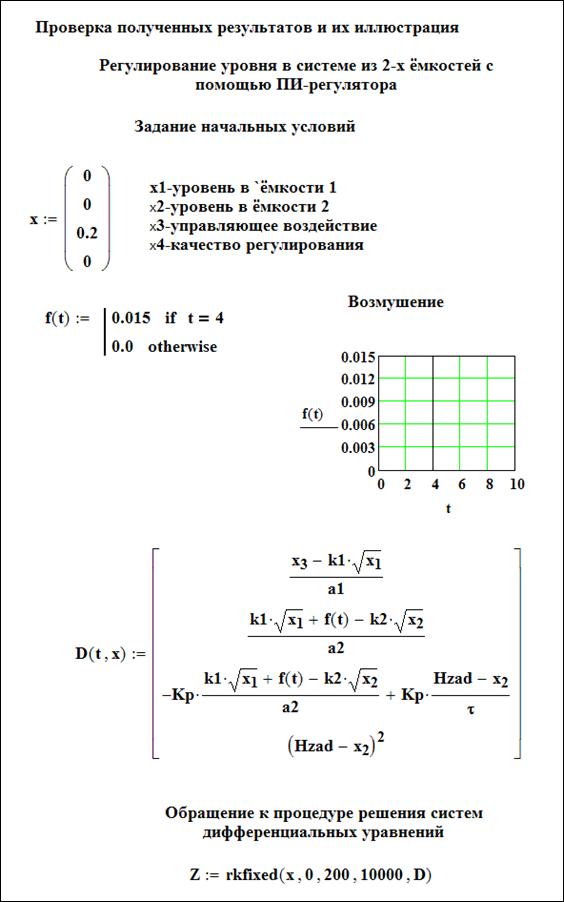
Рисунок 1.5-Проверка полученных результатов

Рисунок 1.6-Результаты моделирования оптимального управления

На рисунке 1.6 представлены результаты моделирования процесса управления уровня в емкости при оптимальных настройках регулятора. Как видно из результатов моделирования значение критерия качества составляет 61.4,при значениях коэффициента пропорциональности равного 2 и времени изодрома -10.3 с. При оптимизации коэффициент пропорциональности был ограничен значением 2,для того чтобы управляющее значение не было слишком большим.

Дата добавления: 2014-11-29