С помощью пи-регулятора при наличии запаздывания

РЕГУЛИРОВАНИЕ ТЕМПЕРАТУРЫ В ЕМКОСТИ

В данном разделе рассматривается задача определения оптимальных настроек ПИ-регулятора температуры жидкости в емкости, с помощью нагревателя. На рисунке 1.1 представлен объект управления и принципиальная схема регулирования температуры жидкости в ёмкости.

Рисунок 3.1 - Принципиальная схема регулирования

температуры жидкости в ёмкости.

Математическое описание объекта управления имеет следующий вид:

Начальные условия при t=0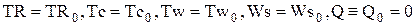

Второе и третье уравнение в системе представляют собой изменение во времени температуры чехла термопары - 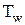и температуры,измеренной с помощью термопары - с учетом запаздываний- .

Уравнение для пропорционально-интегрального регулятора (ПИ) по отклонению может быть представлено в следующем виде:

,

где ошибка регулирования определяется соотношением: .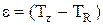

В работе это уравнение представлено в виде дифференциального уравнения в виде:

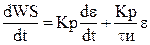
с начальными условиями при t=0 .

Это уравнение входит четвертым в математическое описание объекта управления.

Критерий качества регулирования по отклонению регулируемой величины от заданного значения запишем в следующем виде:

.

Критерий качества записан в дифференциальной форме в виде пятого уравнения в системе уравнений математического описания.

Таблица 3.1 – Спецификация принятых обозначений и их размерность

Обозначения	Наименование	Размерность
Q	Параметр, характеризующий качество регулирования	-
TR	Температура в ёмкости	^0С
WS	Величина, пропорциональная количеству теплоты, подаваемой в реактор (управляющее воздействие)	-
T0	Температура входного потока Т0	^0С
M	Масса жидкости в ёмкости	кг
r	Удельная теплота парообразования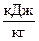
cp	Теплоёмкость
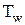
	Температура чехла термопары	^0С
	Температура термопары	^0С

На рисунках 3.2- 3.4 представлены результаты моделирования процесса управления уровня в емкости при некоторых настройках регулятора.

Интегрирование системы дифференциальных уравнений осуществляется с помощью встроенной функции rkfixed.

Рисунок 3.2-Протокол задания исходных данных

Рисунок 3.3-Интегрирование системы дифференциальных уравнений

Как видно из результатов моделирования значение критерия качества составляет более 6000,при значениях коэффициента пропорциональности -0.1 и времени изодрома-6 с.

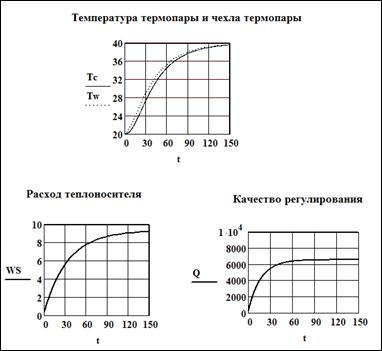
Рисунок 3.4-Результаты моделирования температуры жидкости в емкости

Нахождения оптимальных настроек регулятора. Для исследуемой системы найти такие значения параметров настройки ПИ - регулятора: коэффициент пропорциональности -Kp, время изодрома- 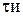,при которых критерий качества регулирования был бы минимальным.

Рисунок 3.5- Протокол задания исходных данных при решении

оптимальной задачи

На рисунках 3.5-3. представлены результаты решения оптимальной задачи.

Рисунок 3.6-Программа для вычисления критерия оптимизации

Рисунок 3.7- Результаты решения оптимальной задачи

Рисунок 3.8-Полученные результаты

Для интегрирования системы дифференциальных уравнений на каждом шаге решения оптимальной задачи воспользуемся методом Эйлера.В соответствие с этим методом система дифференциальных уравнений сводится к решению системы рекуррентных соотношений (см.рисунок 3-6).

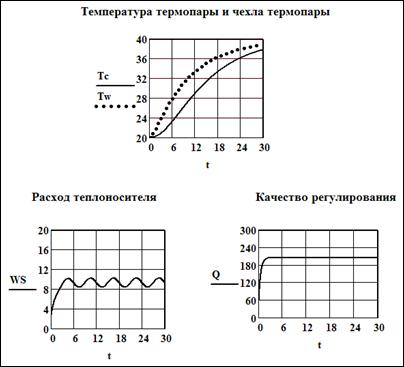
Рисунок 3.9- Полученные результаты

Как видно из результатов вычислений при наличии синусоидального

изменения расхода входного потока система управления при найденных параметрах настройки регулятора коэффициента пропорциональности Kp=16.6 и времени изодрома =1 поддерживает заданное значение температуры в ёмкости.

Дата добавления: 2014-11-29