Основные подходы к изучению движения сплошных сред

Изучение движения жидкости может быть произведено с двух точек зрения.

С точки зрения Лагранжа: объектом изучения служит сама движущаяся жидкость или отдельные ее частицы, рассматриваемые как материальные частицы, сплошным образом заполняющие движущийся объем жидкости. Здесь изучение состоит:

1) в исследовании изменений, которые претерпевают различные векторные и скалярные величины, характеризующие движение некоторой фиксированной частицы жидкого объема (например, скорость, плотность и т.д.) в зависимости от времени;

2) в исследовании изменений тех же величин при переходе от одной частицы жидкого объема к другой. При этом величины, характеризующие движение, рассматриваются как функции времени и тех чисел, которыми отмечается индивидуальность взятой частицы.

За такие числа принимают декартовы координаты жидкой частицы – x₀, y₀, z₀ в некоторый начальный момент времени t₀; Тогда при движении жидкого объема координаты частицы будут

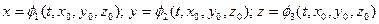(1)

причем при t=t₀ функции φ₁, φ₂, φ₃ тождественно обращаются в x₀, y₀, z₀:

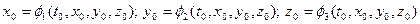
Для x₀, y₀, z₀ имеем:

,

где a, b, c – заданные величины.

По Лагранжу переменные t,a,b,c - аргументы, определяющие значение различных векторных и скалярных функций, которыми характеризуется движение жидкости. Это переменные Лагранжа.

Таким образом, имеем:

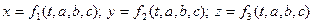(2)

Проекции скорости и ускорения имеют вид:

; (3)

, (4)

плотность будет ρ=f(a,b,c,t) и т.д.

С точки зрения Эйлера объектом изучения является не сама жидкость, а неподвижное пространство, заполненное движущейся жидкостью, и изучается:

1) изменение различных элементов движения в фиксированной точке пространства с течением времени;

2) изменение этих элементов при переходе к другим точкам пространства. Иначе говоря, различные векторные и скалярные элементы движения рассматриваются как функции точки и времени c аргументами x, y, z, t – переменные Эйлера.

Например, v = F (r, t) или

, (5)

и т.д.

Таким образом, по Эйлеру объектами изучения являются различные векторные и скалярные поля, характеризующие движение жидкости, например, поле скорости, поле ускорений, поле плотностей и т.д.

Переход от переменных Лагранжа к переменным Эйлера и обратно может быть осуществлен при помощи уравнений (2), которые должны иметь однозначные решения относительно a,b,c:

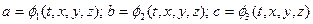(6)

Из взаимной разрешимости уравнений (2) и (6) следует, что ни один из функциональных определителей

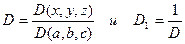
не обращаются в нуль или бесконечность. Пусть, например, некоторая величина A задана в переменных Эйлера A=F(x,y,z,t) и требуется составить ее производные по переменным Лагранжа; тогда имеем:

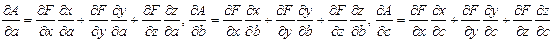; (7)

. (8)

Заметим, что (8) дает выражение для полной или индивидуальной производной функции F:

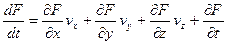. (9)

Применяя (9) к функциям v_x, v_y, v_z, имеем выражения для проекций ускорения в переменных Эйлера:

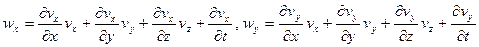
(10)

Обратный переход от переменных Эйлера к переменным Лагранжа может быть произведен при помощи уравнений (5), которые в переменных Лагранжа принимают вид:

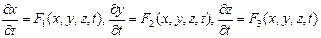. (11)

Интегрируя эти уравнения, найдем

, (12)

где c₁, c₂, c₃ – произвольные постоянные, появляющиеся вследствие интегрирования. Полагая a=c₁, b=c₂, c=c₃, приходим к уравнениям (2), определяющим движение в переменных Лагранжа.

Дата добавления: 2014-11-29