Завдання №8

Завдання №7.

У магазин надходять однакові вироби з трьох заводів, причому 1-ий завод постачає 45% виробів, 2-ий – 35%, 3-ій – 20%. Серед виробів 1–го заводу 85% першосортних, 2-го – 80%, 3-го – 95%. Куплено один виріб. Він виявився першосортним. Визначити ймовірність того, що куплений виріб випущений 3– їм заводом.

Розв'язання.

При розв'язуванні цієї задачі використовуємо формулу Бейеса (11). Знайдемо 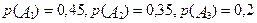- ймовірності того, що куплений виріб виготовлений i-им заводом. Ці події складають повну групу подій. Визначимо умовні ймовірності наступних подій:

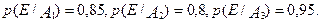
Це ймовірності того, що куплений виріб першосортний, за умови, що він надійшов з i-го заводу. Знайдемо за формулою (10)

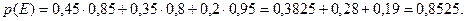
Тоді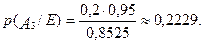

Ймовірність появи деякої події в усякому з 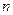незалежних випробувань дорівнює 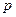=0,2.. Визначити ймовірність того, що число 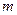появ події задовольнить наступній нерівності: 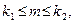якщо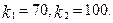

Розв'язання. За умовою, р=0.2; q=0.8; n=400; 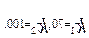Скористаємося інтегральною теоремою Лапласа - формули (15):

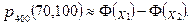
Обчислимо нижню і верхню границі інтегрування:

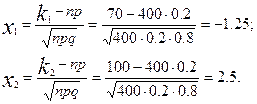
Таким чином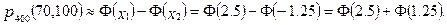

За таблицею додатка знаходимо

Шукана ймовірність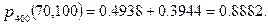

Завдання №9. За даними технологічного контролю в середньому 2% виготовлених на заводі годинників мають потребу в додатковому регулюванні. Знайти ймовірність того, що з 100 годинників:

1. Потребує додаткового регулювання рівно 3 годинника;

2. Потребує додаткового регулювання не більш ніж 3 годинника;

3. Потребує додаткового регулювання не менш ніж 3 годинника.

Розв'язання. Оскільки n=100 велике, а p=0.002 мале, необхідні ймовірності можна знайти за допомогою формули Пуассона, де 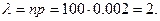Тоді за формулою (14):

1.

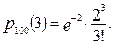
2.

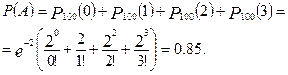
3.

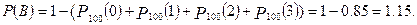
Завдання №10.

Дано густину розподілу 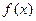випадкової величини 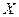, причому 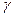- невідомий параметр.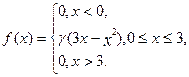

Знайти: 1) параметр 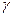; 2) математичне сподівання 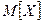, дисперсію 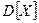; 3) функцію розподілу випадкової величини 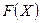; 4) побудувати їхні графіки; 5) знайти ймовірність виконання нерівності .

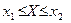Розв'язання.

1) Так як усі значення випадкової величини укладені на відрізку [0,3], то 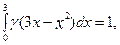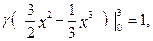звідки 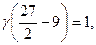тобто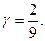

2) Математичне сподівання знайдемо за формулою (23)

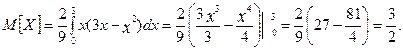
Дисперсію знайдемо за формулою (24). Для цього за формулою (26) знайдемо

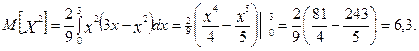
За формулою (24) 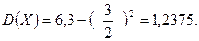Знайдемо ще за формулою (27)

3) Функцію розподілу знайдемо, використовуючи оизначення (16).

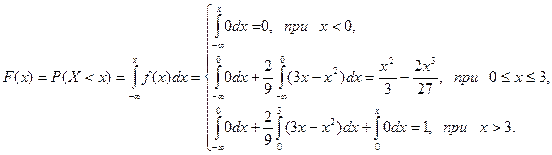
Остаточно одержуємо, що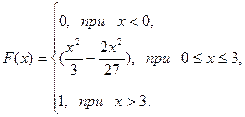

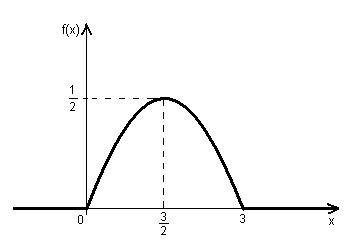
Графіком функції f(x) в інтервалі (0,3) є парабола 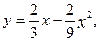а поза цим інтервалом графік співпадає з віссю абсцис.

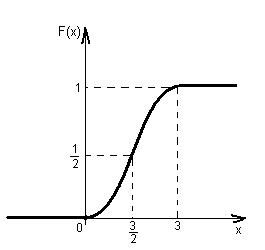
4. Графік функції F(x)

5. Ймовірність влучення випадкової величини X у проміжок (1,2) знайдемо з рівності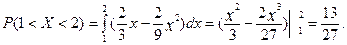

Дата добавления: 2014-11-29