Завдання №14. 1 страница

Нехай у результаті випробувань випадкова величина X прийняла значення з частотами 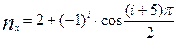, i=1,2,3,…,10,... Потрібно:

а) скласти таблицю статистичного розподілу, розбивши проміжок (0,50) на десять ділянок однакової довжини, побудувати гістограму відносних частот, а також визначити середнє значення, дисперсію і середнє квадратичне відхилення цієї випадкової величини.

б) вирівняти ці дані випробувань, застосовуючи закон розподілу з рівномірною густиною.

в) перевірити, чи узгоджується даний статистичний розподіл з теоретичним, застосовуючи критерії згоди Пірсона і Романовського.

Розв'язання. а) перш за все складемо значення величин 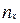у вигляді таблиці

I	(0,5)	(5,10)	(10,15)	(15,20)	(20,25)	(25,30)	(30,35)	(35,40)	(40,45)	(45,50)

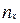
Обсяг вибірки n=21.

Статистичний розподіл має вигляд:

I	(0,5)	(5,10)	(10,15)	(15,20)	(20,25)	(25,30)	(30,35)	(35,40)	(40,45)	(45,50
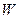
	1/7	2/21	1/21	2/21	1/7	2/21	1/21	2/21	1/7	2/21

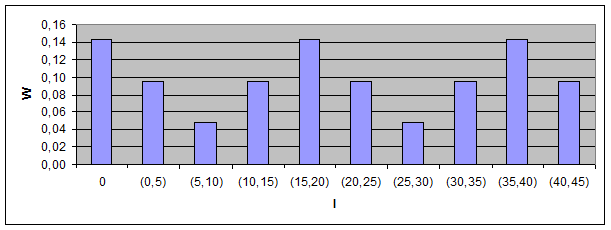
Гістограма відносних частот.

Середнє значення випадкової величини X для вибірки знайдемо за формулою

.

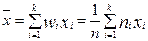Статистичну дисперсію випадкової величини, заданої статистичним розподілом, знайдемо за формулою , а середнє квадратичне відхилення .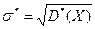

Знайдемо

Тоді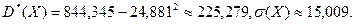

б) Із зростанням обсягу вибірки n середнє значення 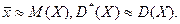Тому маємо .

Складемо систему лінійних рівнянь для рівномірного закону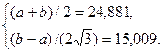

Розв′яжемо останню систему, знайдемо a=-1,1153, b=50.877, звідки 1/(b-a)=0,019.

Отже, теоретичний розподіл має рівномірну густину

в) Перевіримо, чи узгоджується даний статистичний розподіл з отриманим теоретичним, що має рівномірну густину. Для цього знайдемо ймовірності влучення випадкової величини, розподіленої за отриманим законом з рівномірною густиною в інтервали(-5,0),(0,5),…,(50,55):

(-5,0)	(0,5)	(5,10)	(10,15)	(15,20)	(20,25)	(25,30)	(30,35)	(35,40)	(40,45)	45,50)	(50,5) (50,55)
,021	0,095	0,095	0,095	0,095	0,095	0,095	0,095	0,095	0,095	0,095	0,017

Складемо розрахункову таблицю для обчислення :

W	P	W-P
	0,021	-0,021	0,000441	0,021
0,1429	0,095	0,0479	0,002294	0,02415
0,0952	0,095	0,0002	0,00000004	0,00000042
0,0476	0,095	-0,0474	0,00224676	0,02365
0,0952	0,095	0,0002	0,00000004	0,00000042
0,1429	0,095	0,0479	0,002294	0,02415
0,0952	0,095	0,0002	0,00000004	0,00000042
0,0476	0,095	-0,0474	0,00224676	0,02365
0,0952	0,095	0,0002	0,00000004	0,00000042
0,1429	0,095	0,0479	0,002294	0,02415
0,0952	0,095	0,0002	0,00000004	0,00000042
	0,017	-0,017	0,000289	0,017

Знайдемо за формулою 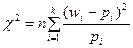. Отже, 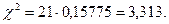У нашій задачі використовується число розрядів статистичної таблиці l=12, число умов, що накладаються на частоти t=3, тому що використовуються наступні три умови:

де - математичне сподівання і дисперсія в теоретичному законі розподілу. Визначимо число ступенів вільності r = l – t = 12 – 3 = 9. Тоді у таблиці (див. підручник) знаходимо: якщо то p=0,9643; якщо 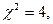то p=0,9114. Звідки 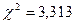. Знайдемо

Отже, можна сказати, що заданий статистичний розподіл цілком узгоджується із законом розподілу, що має рівномірну густину. За критерієм згоди Пірсона, якщо 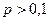, то можна зробити висновок, що гіпотеза про прийнятий теоретичний розподіл не суперечить даним випробувань.

За критерієм В.І. Романовського, якщо величина , то розбіжність теоретичних та практичних випробувань можна вважати невипадковою. У нас тобто розбіжність теоретичних та практичних випробувань можна вважати випадковою.

Завдання №.15.

Випадкова величина Х має нормальний розподіл з відомим середнім квадратичним відхиленням . Знайти довірчі інтервали для оцінки невідомого математичного сподівання a по вибірковим середньої 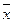, якщо обсяг вибірки n=36 і задана надійність оцінки .

Розв'язання. Довірчий інтервал, що покриває параметр 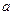із надійністю 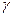, одержимо зі співвідношення ; точність оцінки . Знайдемо t. Із співвідношення одержимо

З таблиці додатку знаходимо

Знайдемо

Довірчий інтервал буде такий: 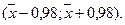Наприклад, якщо , то довірчий інтервал має наступні довірчі границі:

Таким чином, Значення невідомого параметру 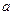, погоджуючись з данними вибірки, задовольняють нерівності

4.4. Варіанти задач до розрахунково-графічної роботи № 6.

Завдання №1.

Кидаються два гральних кубики. Необхідно:

1. Описати простір елементарних подій;

2. Указати склад підмножин, що відповідають подіям:

а) A= {сума очок кратна N};

б) B= { сума очок непарна};

в) C={ сума очок кратна N чи непарна};

г) D={ сума очок кратна N і парна};

д) A+B, BC, ;

3. Визначити ймовірність того, що:

а) сума числа очок не перевершує N;

б) добуток числа очок не перевершує N:

в) добуток числа очок ділиться на N.

Вар-ты

N

Вар-ты

N

Завдання №2.

Є вироби чотирьох сортів: виробів 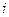- го сорту є , 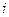=1,2,3,4. Для контролю навмання беруть 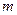виробів. Визначити ймовірність того, що серед них першого сорту, другого, третього і четвертого сорту відповідно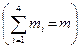

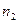
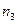
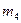
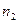
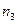
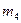
Завдання №3.

Серед 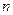лотерейних квитків 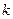виграшних. Навмання взяли 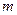квитків. Визначити ймовірність того, що серед них 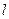виграшних.

n

l

m

k

n

l

m

k

Завдання №4.

У двох партіях і доброякісних виробів відповідно. Навмання вибирають по одному виробу з кожної партії. Яка ймовірність знайти серед них:

а) хоча б один бракований;

б) два бракованих;

в) один доброякісний й один бракований.

Завдання №5.

З 1000 ламп належать 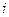- ій партії, 1,2,3, . У першій партії 7% бракованих ламп, у другий – 5 %, у третій – 6%. Навмання вибирається одна лампа. Визначити ймовірність того, що обрана лампа – бракована.

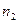
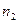
Завдання №6.

У першій шухляді білих і 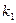чорних куль, у другій - 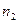білих і 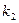чорних куль. З першої шухляди в другу переклали 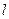куль, потім із другої шухляди витягнута одна куля. Визначити ймовірність того, що обрана із другої шухляди куля – чорна.

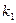
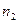
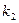
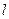
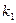
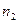
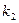
Дата добавления: 2014-11-29