Завдання № 12

Дискретна випадкова величина X має тільки два можливих значення, і , причому . Ймовірність того, що вона прийме значення дорівнює 0,6.

Знайти закон розподілу величини X, якщо математичне сподівання і дисперсія відомі: М(Х)=1,4, D(Х)=0,24.

Розв′язання.

Так як , то ймовірність того, що випадкова величина X прийме значення х₂, дорівнює Р₂= 1-0,6=0,4. Запишемо закон розподілу X:

X	x1	x2
P	0,6	0,4

Для відшукання і складемо два рівняння, виражаючи математичне сподівання і дисперсію через і .

Маємо

і, отже,

Далі

Враховуючи те, що D(X)=0,24, одержимо рівняння

Отже, маємо систему рівнянь

Розв′яжемо її, одержимо:

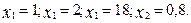
За умовою 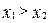, тому задачі задовольняє перший розв'язок.

Шуканий закон розподілу має вид:

X
P	0,6	0,4

Завдання №13. У двох шухлядах знаходяться по шість кульок; у 1-ій шухляді: одна куля з №1,дві кулі — з № 2, три кулі з №3; у 2-ій шухляді: дві кулі -з № 1, три кулі -з № 2, одна куля -з № 3. Нехай X — номер кулі, вийнятої з першої шухляди, У-номер кулі, вийнятої з другої шухляди. З кожної шухляди вийняли по кулі.

1.Скласти таблицю закону розподілу системи випадкових величин (X, Y);

2.Знайти математичні сподівання і дисперсії випадкових величин X і Y;

3. Знайти коефіцієнт кореляції цих випадкових величин.

Розв'язання.

Випадкова точка (1;1) має кратність 1*2=2,тому що в 1-ій шухляді куль з №1 одна, у 2-ої шухляді куль з №1 дві. Тоді згідно основного принципу комбінаторики кількість наслідків дорівнює 1*2=2.

Аналогічно, випадкова точка (1,2) має кратність 1*3=3;

(1,3) - 1*1=1;

(2,1) - 2*2=4;

(2,2) - 2*3=6;

(2,3) - 2*1=2;

(3,1) - 3*2=6;

(3,2) - 3*3=9;

(3,3) - 3*1=3.

Усього випадкових точок 6*6=36. Так як відношення кратності точки до всієї кількості точок дорівнює ймовірності появи цієї точки, то таблиця закону розподілу системи випадкових величин має вид:

Х Y
	1/18	1/12	1/36
	1/9	1/6	1/18
	1/6	¼	1/12

Сума всіх ймовірностей, зазначених у таблиці, дорівнює одиниці.

1. Знайдемо математичні сподівання випадкових величин Xі Y.

Маємо:

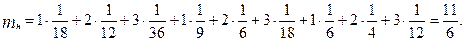
2. Знайдемо дисперсії випадкових величин Xі В:

Звідси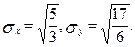

3. Знайдемо коефіцієнт кореляції:

Тому що , то і коефіцієнт кореляції .

Елементи математичної статистики

Дата добавления: 2014-11-29