Завдання №14. 2 страница

Завдання №7.

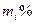У магазин надходять однотипні вироби з трьох заводів, причому завод поставляє виробів ( 1,2,3) Серед виробів i – го заводу 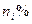першосортних. Куплено один виріб. Він виявився першосортним. Визначити ймовірність того, що куплений виріб було випущено j – им заводом.

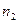
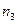
J

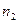
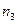
J

Завдання №8.

Ймовірність того, що відбулася деяка подія в кожному з 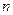незалежних випробувань дорівнює 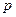. Визначити ймовірність того, що число 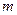того, що подія відбулася, задовольнить наступній нерівності:

а) варіанти 1 – 11: ;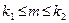

б) варіанти 12 – 21: 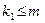(не менше, ніж );

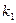в) варіанти 22 – 30: (не більше, ніж ).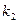

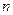
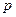
	0.8	0.8	0.8	0.7	0.7	0.7	0.7	0.6	0.75	0.75	0.75	0.7	0.7	0.7	0.6

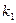
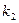
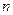
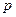
	0.6	0.6	0.8	0.8	0.8	0.8	0.3	0.3	0.3	0.4	0.4	0.4	0.8	0.6	0.8

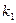
Завдання №9.

За даними технологічного контролю в середньому n% виготовлених на заводі годинників мають потребу в додатковому регулюванні. Знайти ймовірність того, що з N годинників:

1. додаткового регулювання потребують рівно k годинників;

2. додаткового регулювання потребують не більш k годинників;

3. додаткового регулювання потребують не менш k годинників.

№

n%

N

k

№

n%

N

k

Завдання №10.

Дано густину розподілу 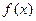випадкової величини 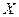. Знайти параметр 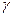, математичне сподівання 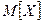, дисперсію 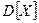, функцію розподілу випадкової величини 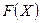, побудувати їхні графіки, знайти ймовірність виконання нерівності .

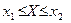а) варіант 1- 8: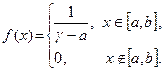

б) варіант 9 – 16: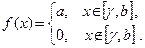

в) варіант 17– 24:

г) варіант 25 – 31:

A	2.5	1.5	1.2		-1	-2	-.5
B			2.5	3.5			2.5	1.8	2.4	3.5	2.8	2.8	2.6	2.6
x	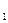				-.7	-3	-1	1.3	1.5	2.5		-1	1.5	1.4
x	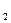3.3	2.6	2.3	2.8	1.1	-2		1.6			2.5

A		-4	-3				-1	-.5	-.5	0.5	0.2	0.5	0.4	1.4
B	4.8	-2	-1			1.5	1.5	-1
x	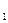4.5	-1	-1					-1	-1
x	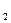					0.5						0.5

Завдання №11.

ВАРІАНТ1.

Ймовірність влучення в ціль при одному пострілі для даного стрільця дорівнює 0,8. Стрілець робить 3 постріли. Скласти закон розподілу випадкової величини X - числа влучень у ціль. Знайти математичне сподівання і дисперсію випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 2.

Ймовірність влучення в ціль при одному пострілі для даного стрільця дорівнює 0,9. Скласти закон розподілу випадкової величини X - числа влучень у ціль при двох пострілах. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРИАНТЗ.

Гральна кістка кинута 3 рази. Скласти закон розподілу випадкової величини X - числа появи шістки. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 4.

Гральна кістка кинута 2 рази. Скласти закон розподілу випадкової величини X - числа появи двійки. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 5.

Гральна кістка кинута 4 рази. Скласти закон розподілу випадкової величини X - числа появи трійки. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 6.

Скласти закон розподілу імовірностей числа появи події А в трьох незалежних випробуваннях, якщо ймовірність появи події в кожному випробуванні дорівнює 0,6, знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 7.

Монета кидається 3 рази. Скласти закон розподілу випадкової величини X - числа появи герба.. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 8.

Монета кидається 2 рази. Скласти закон розподілу випадкової величини X - числа появи герба.. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 9.

Монета кидається 4 рази. Скласти закон розподілу випадкової величини X - числа появи герба.. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 10.

Монета кидається 5 разів. Скласти закон розподілу випадкової величини X - числа появи герба.. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 11.

Монета кидається 6 разів. Скласти закон розподілу випадкової величини X - числа появи герба.. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 12

Виконується 4 постріли по мішені. Ймовірність влучення при кожному пострілі дорівнює 0,8. Скласти закон розподілу випадкової величини X - числа влучень у мішень. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 13.

По мішені ведуться постріли до першого влучення або до витрати всіх патронів. Скласти закон розподілу випадкової величини X — числа витрачених патронів, якщо ймовірність влучення при окремому пострілі дорівнює 0,8, а число наявних патронів 3. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 14.

По мішені ведуться постріли до першого влучення або до витрати всіх патронів. Скласти закон розподілу випадкової величини X - числа витрачених патронів, якщо ймовірність влучення при кожному пострілі дорівнює 0,6, а число наявних патронів 4. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 15.

По мішені ведуться постріли до першого влучення або до витрати всіх патронів. Скласти закон розподілу випадкової величини X - числа витрачених патронів, якщо ймовірність влучення при кожному пострілі дорівнює 0,8, а число наявних патронів 5. Знайти математичне сподівання і дисперсію цієї величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 16.

По мішені ведуться постріли до першого влучення або до витрати всіх патронів. Скласти закон розподілу випадкової величини X - числа витрачених патронів, якщо ймовірність влучення при кожному пострілі дорівнює 0,85, а число наявних патронів 4. Знайти математичне сподівання і дисперсію цієї величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 17.

Ймовірність влучення в мішень при одному пострілі для даного стрільця дорівнює 0,5. Скласти закон розподілу випадкової величини X - числа влучень у мішень при 5 пострілах. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 18.

Скласти закон розподілу випадкової величини X - числа появи події А в 2 незалежних випробуваннях, якщо ймовірність появи події в кожному випробуванні дорівнює 0,3. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 19.

Скласти закон розподілу випадкової величини X - числа появи події А в трьох незалежних випробуваннях, якщо ймовірність появи події в кожнім випробуванні дорівнює 0,1, знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 20.

Скласти закон розподілу випадкової величини X - числа появи події А в чотирьох незалежних випробуваннях, якщо ймовірність появи події в кожному випробуванні дорівнює 0,4. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 21.

У партії 10% нестандартних деталей. Навмання відібрані три деталі. Скласти закон розподілу випадкової величини X - числа нестандартних деталей серед трьох відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 22.

У партії 10% нестандартних деталей. Навмання відібрані дві деталі. Скласти закон розподілу випадкової величини X - числа нестандартних деталей серед двох відібраних. Знайти математичне сподівання.і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 23.

У партії з 8 деталей маємо 6 стандартних. Навмання відібрані дві деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед двох відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 24.

У партії з 8 деталей маємо 6 стандартних. Навмання відібрані три деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед трьох відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 25.

У партії з 6 деталей маємо 4 стандартних. Навмання відібрані дві деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 26.

По мішені ведуться постріли до першого влучення або до витрати всіх патронів. Скласти закон розподілу випадкової величини X - числа витрачених патронів, якщо ймовірність влучення при кожнім пострілі дорівнює 0,75, а число наявних патронів 3. Знайти математичне сподівання і дисперсію цієї величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 27.

По мішені ведуться постріли до першого влучення або до витрати всіх патронів. Скласти закон розподілу випадкової величини X - числа витрачених патронів, якщо ймовірність влучення при кожнім пострілі дорівнює 0,6, а число наявних патронів 4. Знайти математичне сподівання і дисперсію цієї величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 28.

У партії з 7 деталей маємо 4 стандартних. Навмання відібрані три деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 29.

У партії з 6 деталей маємо 3 стандартних. Навмання відібрані три деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ВАРІАНТ 30.

У партії з 8 деталей маються 4 стандартних. Навмання відібрані три деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед відібраних. Знайти математичне сподівання і дисперсію цієї випадкової величини. Знайти функцію розподілу F(x) і накреслити її графік.

ЗАВДАННЯ 12.

Дискретна випадкова величина X має тільки два можливих значення, і , причому . Ймовірність того, що вона прийме значення дорівнює p. Знайти закон розподілу величини X, якщо математичне сподівання M(X) і дисперсія D(X) відомі.

ВАРІАНТИ ДО ЗАВДАННЯ

№вар.	P	M(X)	D(X)	№ вар.	P	M(X)	D(X)
	0,5	3,5	0,25		0,8	1,4	0,64
	0,5				0,8	1,6	1,44
	0,1	1,9	0,09		0,8	1,8	2,56
	0,2	2,6	0,64		0,8
	0,5	5,5	0,25		0,6	1,4	0,24
	0,2	1,8	0,16		0,6	1,8	0,96
	0,2	2,8	0,16		0,6	2,2	2,16
	0,1	2,8	0,36		0,6	2,6	3,84
	0,4	2,2	0,96		0,5	1,5	0,25
	0,5	2,5	2,25		0,5
	0,9	1,4	1,44		0,5	3,5	0,25
	0,9	1,1	0,09		0,5
	0,9	1,2	0,36		0,1	1,9	0,09
	0,9	1,3	0,81		0,2	2,6	0,64
	0,8	1,2	0,16		0,5	5,5	0,25

Дата добавления: 2014-11-29