
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Центр паралельних сил та центр ваги
|
|
|
|
В даній темі при її вивченні необхідно звернути увагу на послідовне складання паралельних сил.
Розглянути поняття центр паралельних сил та центр ваги твердого тіла і плоскої фігури.
Ознайомитись із способами визначення координат центра ваги тіла.
Вивчити формули радіуса вектора і координат центра паралельних сил і порядок знаходження центра ваги елементарних плоских фігур.
Розглянути приклад розв’язання задач з використанням формул для знаходження центра ваги плоскої фігури.
Приклад. Визначити координати центра ваги однорідної пластини. Розміри в мм задані на рис. 5.
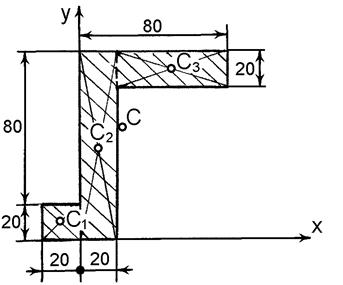 (М 1:2)
(М 1:2)
рис. 5
Розв'язання.
Покажемо осі координат 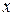 і
і 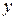 . Розбиваємо пластину на частини, які утворені трьома прямокутниками. Для кожного прямокутника проводимо діагоналі, точки перетину яких
. Розбиваємо пластину на частини, які утворені трьома прямокутниками. Для кожного прямокутника проводимо діагоналі, точки перетину яких 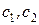 і
і 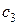 відповідають центрам ваги кожного прямокутника. У прийнятій системі координат неважко отримати значення координат цих точок. А саме:
відповідають центрам ваги кожного прямокутника. У прийнятій системі координат неважко отримати значення координат цих точок. А саме: 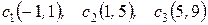 . Площі кожного тіла відповідно дорівнюють: І –
. Площі кожного тіла відповідно дорівнюють: І – 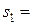 4
4 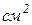 ; ІІ –
; ІІ – 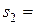 20
20 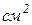 ;
;
ІІІ – 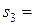 12
12 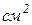 . Площа всієї пластини дорівнює:
. Площа всієї пластини дорівнює: 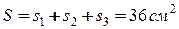 .
.
Для визначення координат центра ваги заданої пластини використаємо вираз (1.159). Підставимо значення всіх відомих величин у дані рівняння, отримаємо
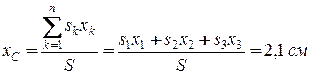 ,
,
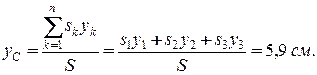
За обчисленими значеннями координат центра ваги пластини можна позначити точку  на рисунку. Як бачимо, центр ваги (геометрична точка) пластини розташований за її межами.
на рисунку. Як бачимо, центр ваги (геометрична точка) пластини розташований за її межами.
При розгляді даної теми необхідно використовувати посібник: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 94 – 110.
Теоретичні відомості
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1024; Нарушение авторских прав?; Мы поможем в написании вашей работы!