Центр паралельних сил та центр ваги. 1. Послідовне складання паралельних сил

1. Послідовне складання паралельних сил. Центр паралельних сил.

2. Формули радіуса вектора і координат центра паралельних сил.

3. Центр ваги твердого тіла і плоскої фігури.

Література

1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.

2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.

1. Послідовне складання паралельних сил. Центр паралельних сил.

Припустимо, що до тіла у точках прикладена система паралельних і однаково спрямованих сил (рис.1) додамо геометрично сили 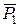і , тобто визначимо їх рівнодійну 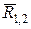. Вона буде дорівнювати

. (1.139)

Рис. 2.

Точка 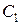прикладання цієї рівнодійній 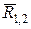визначається за відомим правилом додавання двох паралельних сил, які мають однаковий напрямок. Оскільки сили 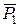і прикладені у точках і 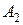, то, з'єднавши ці точки прямою, можна відшукати положення точки 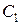на цій прямій за відомим рівнянням

. (1.140)

Далі аналогічно додамо сили 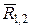і 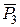, отримуючи їх рівнодійну , яка є фактично рівнодійною трьох сил і буде дорівнювати

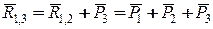. (1.141)

Точка прикладання цієї рівнодійної також визначається за вказаним вище правилом на прямій .

Таким же чином поводимося з рештою сил, послідовно їх додаючи, і остаточно отримаємо рівнодійну 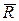системи паралельних сил. Вона буде прикладеною в точці 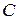, спрямована у той же бік, що і задані паралельні сили, величина її буде дорівнювати

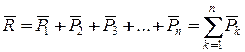. (1.142)

Повернемо всі задані сили навколо їх точок прикладання в один бік на один і той же кут і тепер знайдемо їх рівнодійну. Також починаємо з додавання сил 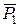і . Але, як бачимо з рис. 1.56, а також з рівнянь (1.139) і (1.140), ні модуль рівнодійної 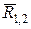, ні положення точки її прикладання 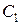на прямій 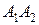, не змінюються. Змінюється лише напрямок, який буде паралельним новому напрямку сил.

Якщо провести до кінця додавання паралельних сил, які вже мають новий напрямок, то будемо бачити, що і рівнодійна 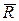у даному випадку не змінює ні свого модулю, ні положення точки прикладання 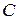. Змінюється лише напрямок її лінії дії.

Таким чином, точка прикладання рівнодійної 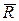системи паралельних сил завжди співпадає з точкою 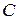, положення якої по відношенню до положення точок , або, взагалі, до тіла завжди буде незмінним. Ця точка має назву центра паралельних сил.

Центр паралельних сил – це точка прикладання їх рівнодійної, яка не змінює свого положення при повороті усіх сил на один і той же кут, в один і той же бік.

2. Формули радіуса вектора і координат центра паралельних сил.

Припустимо, що до тіла у точках прикладена система паралельних сил , яка зведена до рівнодійної сили 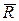, що прикладена у точці 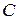(рис. 2). Виберемо просторову декартову систему координат 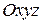так, щоб б одна з осей (наприклад, вісь 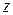) була паралельна заданим силам. Знайдемо моменти усіх сил відносно осей координат і .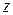

Рис. 2.

Позначимо у прийнятій системі координат координати точок прикладання сил 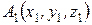, , 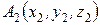,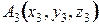..., і – точка прикладання рівнодійної .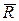

Обчислимо спочатку моменти всіх сил відносно осі 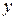. Оскільки

,

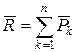то за теоремою Вариньона

,

а тому

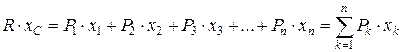. (1.143)

Звідки координата буде дорівнювати

. (1.144)

Аналогічно визначимо моменти усіх сил відносно осі 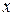. Матимемо

, (1.145)

звідки координата 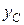буде дорівнювати

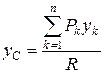. (1.146)

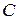Далі повернемо всі сили на один і той же кут в один бік (наприклад, на кут 90^о, перпендикулярно до площини ). Положення точки , як відомо, при повороті усіх сил на один і той же кут, в один і той же бік не змінюється. Також обчислимо моменти усіх сил відносно осі 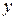. Матимемо

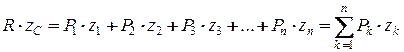, (1.147)

звідки координата буде дорівнювати

. (1.148)

Таким чином, остаточно отримаємо формули для координат центра паралельних сил

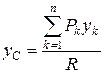, , . (1.149)

3. Центр ваги твердого тіла і плоскої фігури.

На довільну частинку тіла, яке розміщене поблизу поверхні землі, діє сила, що має вертикальний донизу напрямок і яка має назву сила ваги (або просто ваги). Якщо вважати радіус землі достатньо великим (6,4 тис. км), то для тіл, розміри яких у порівнянні з цим радіусом є малими, сили вали (тяжіння), що діють на частинки тіла, можна вважати паралельними, вони зберігають свою власну величину, незважаючи на будь-які повороти тіла.

Рис. 3.

Маємо тіло, яке умовно можна поділити на декілька частин (рис. 1.58). Кожна частина має силу ваги 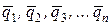. Як бачимо, це є система паралельних сил, рівнодійну якої можна знайти. Використовуючи (1.142), визначаємо цю рівнодійну

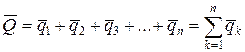. (1.150)

При будь-якому повороті тіла сили 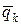залишаються прикладеними до тих же самих точок і залишаються паралельними між собою. Змінюється лише напрямок цих сил по відношенню до тіла. А тому рівнодійна буде при довільному повороті тіла прикладена у точці, яка є центром паралельних сил. Ця точка має назву центра ваги тіла.

Таким чином, центр ваги тіла – це точка, яка незмінно пов'язана з цим тілом, в якій прикладена сила тяжіння тіла і яка не змінює свого положення при повороті тіла на довільний кут.

Визначимо координати центра ваги як центра паралельних сил 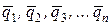на підставі виразів (1.149), а саме

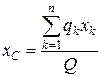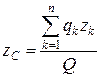, , , (1.151)

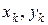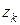де і - координати прикладання сили тяжіння частини тіла .

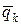Якщо тіло є однорідним, то вага кожної частини пропорційна її об'єму, а саме

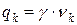, (1.152)

де 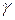- питома вага (вага одиниці об'єму); 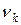- об'єм частини тіла.

вага усього тіла визначається за такою формулою

, (1.153)

де 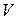- об'єм тіла; 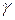- питома вага тіла.

Тепер підставимо (1.152) і (1.153) у (1.151). Причому питома вага 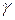, як загальний множник, скорочується. Отримаємо:

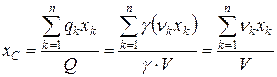. (1.154)

Аналогічно поводимось і при визначенні двох інших координат. остаточно матимемо координати центра ваги об'єму:

, , . (1.155)

Як бачимо, центр ваги однорідного тіла залежить тільки від його геометричної форми. А тому, вираз (1.155) носить назву – центр ваги об'єму.

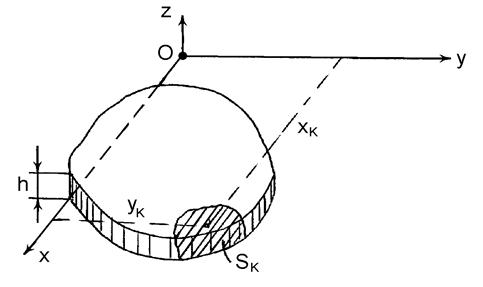
Рис. 4

Тепер, якщо розглядати тіло, яке є пластиною (рис. 4), товщина якої відносно мала, то координата центра її ваги буде дорівнювати . Для визначення двох інших координат використаємо вирази (1.151). Пластину треба уявити у вигляді декількох частин, які мають власну вагу. Далі вважаємо, що вага кожної частки пластини буде дорівнювати

, (1.156)

де 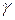- питома вага (вага одиниці об'єму); - товщина пластини;
- площа частини пластини.

Вага всієї пластини буде дорівнювати

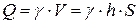, (1.157)

де - площа пластини.

Тепер підставимо (1.156) і (1.157) у перші два вирази (1.151). Зробимо це спочатку для координати , отримаємо

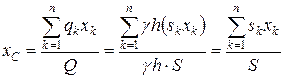. (1.158)

таким же чином обчислимо значення і другої координати 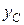. Остаточно матимемо координати центра ваги тонкої пластини

, . (1.159)

Точка, координати якої визначаються формулами (1.159), має назву центра ваги площі.

В результаті вивчення теми слухачі повинні

Знати:

- послідовне складання паралельних сил;

- поняття центр паралельних сил та центр ваги твердого тіла і плоскої фігури;

- способи визначення координат центра ваги тіла;

- формули радіуса вектора і координат центра паралельних сил;

- порядок знаходження центра ваги елементарних плоских фігур.

Вміти:

- розв’язувати задачі з задач з використанням формул для знаходження центра ваги плоскої фігури.

Питання для самоперевірки:

1. Що називають центром паралельних сил?

2. За якими формулами визначаються координати центра паралельних сил?

3. За якими формулами визначаються положення центра ваги тіла, об'єму і площі?

4. Що таке центр ваги тіла?

5. Які існують способи визначення координат центра ваги тіла?

6. Як визначити координати центра ваги дуги кола?

7. Як визначити координати центра ваги трикутника?

8. Як визначити координати центра ваги сектора?

Висновок по темі: Таким чином, центр ваги тіла – це точка, яка незмінно пов'язана з цим тілом, в якій прикладена сила тяжіння тіла і яка не змінює свого положення при повороті тіла на довільний кут.

Центр паралельних сил – це точка прикладання їх рівнодійної, яка не змінює свого положення при повороті усіх сил на один і той же кут, в один і той же бік.

2. Кінематика

2.1 Кінематика точки

Під час вивчення даної теми необхідно ознайомитись з основні поняттями та визначення в кінематиці.

Вивчити способи опису руху точки: векторний, координатний, натуральний.

Розглянути основні кінематичні характеристики руху точки: швидкість і прискорення.

Опрацювати приклад розв’язання задач з визначення траєкторії руху точки.

Дата добавления: 2014-11-29