
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кільця та поля
|
|
|
|
Групи
Півгрупи
Множина Х із заданою на ній бінарною асоціативною операцією називається півгрупою. Півгрупу з нейтральним елементом прийнято називати моноїдом або просто півгрупою з одиницею.
Наведемо деякі приклади півгруп та півгруп з одиницею (моноїдів).
1) Нехай Ω - довільна множина й М(Ω) - множина всіх її перетворень (відображень Ω в себе). Задамо на М(Ω) операцію, яка є природною композицією відображень. Тоді М(Ω) стає некомутативною півгрупою з одиницею. Нейтральним елементом є тотожне відображення.
2) Множина матриць з дійсними значеннями Мn(R) розміру n x n відносно множення матриць є некомутативним моноїдом з нейтральним елементом – одиничною матрицею;
3) Нехай знову Ω - довільна множина й Р(Ω) - множина всіх підмножин цієї множини. Задаємо на Р(Ω) операцію перетину множин. Тоді Р(Ω) стає комутативним моноїдом. Нейтральним елементом тут є множина Ω.
4) Множина цілих чисел, які діляться на деяке фіксоване натуральне число n > 1, відносно операції множення утворює комутативну півгрупу без одиниці.
Півгрупа з одиницею, в якій для кожного елемента існує обернений, називається групою.
Іншими словами, групою називається множина G, на якій задана бінарна операція (символ операції пропускаємо) з наступними властивостями:
(G1) операція асоціативна: (x y) z = x (y z) для всіх x, y, z Î G;
(G2) G містить нейтральний (одиничний) елемент е: e x = x e = x для всіх x Î G;
(G3) для кожного елемента x Î G існує обернений x -1, x -1 x = x x -1= e.
Група, в якій операція є комутативною, тобто для будь-яких x, y Î G виконується умова x y = y x, називається комутативною (абелевою) групою.
Група називається скінченною, якщо вона має скінченне число елементів. У протилежному випадку група називається нескінченною. Якщо група G скінченна, то число її елементів позначається | G | і називається порядком групи.
З аксіом групи (G1) - (G3) випливають наступні прості наслідки.
1. Закон скорочення: якщо x y = x z, то y = z (ліве скорочення);
якщо y x = z x, то y = z (праве скорочення);
2. Для кожного елемента групи обернений елемент єдиний;
3. Для кожної пари елементів a, b Î G рівняння a x = b та y a = b мають єдині розв’язки.
Наступні множини є групами відносно вказаних операцій:
1) множина Z цілих чисел відносно додавання;
2) множини Q \ { 0 }, R \ { 0 }, C \ { 0 } відносно множення. Позначатимемо ці групи відповідно Q*, R*, C*;
3) множини Q, R, C відносно додавання;
4) множина Cn коренів n -го степеня з одиниці відносно множення;
5) множина Aut(M) всіх бієктивних відображень множини M на себе. Якщо множина M є скінченною і має n елементів, то в цьому випадку вказані бієктивні відображення називаються підстановками n елементів, а множина Sn всіх підстановок утворює групу підстановок n елементів;
6) множина GLn(C) невироджених (тобто з відмінним від нуля визначником) комплексних матриць розміру n x n відносно множення матриць.
Зауважимо, що для кожного натурального числа n можна збудувати абелеву групу, яка має порядок n. Для цього треба розглянути фактор-множину Zn = { 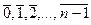 } класів еквівалентності цілих чисел, порівняних за модулем n. Перетворимо цю множину в групу, задавши на ній операцію додавання Å класів цілих чисел за модулем n. Щоб додати два класи
} класів еквівалентності цілих чисел, порівняних за модулем n. Перетворимо цю множину в групу, задавши на ній операцію додавання Å класів цілих чисел за модулем n. Щоб додати два класи 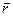 і
і 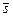 потрібно спочатку додати цілі числа r і s, а потім знайти остачу від ділення знайденої суми на число n. Клас знайденої остачі й буде результатом додавання класів
потрібно спочатку додати цілі числа r і s, а потім знайти остачу від ділення знайденої суми на число n. Клас знайденої остачі й буде результатом додавання класів 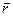 і
і 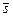 . Множина Zn разом із заданою на ній операцією додавання Å є абелевою групою, яка має порядок n.
. Множина Zn разом із заданою на ній операцією додавання Å є абелевою групою, яка має порядок n.
Далі наведено таблицю Келі для операції додавання Å групи Z 5:
| Å | 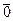
| 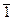
| 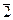
| 
| 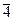
|
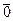
| 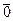
| 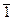
| 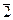
| 
| 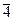
|
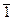
| 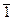
| 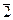
| 
| 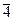
| 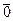
|
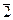
| 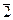
| 
| 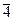
| 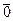
| 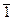
|

| 
| 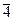
| 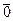
| 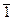
| 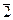
|
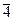
| 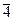
| 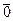
| 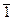
| 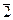
| 
|
Непорожня підмножина Н групи G називається підгрупою, якщо вона є групою відносно визначеної в групі G операції.
Зауважимо, що не всяка підмножина А групи G є підгрупою. Розглянемо, наприклад, підмножину A = { 1, i} групи C4 = { 1, -1, i, -i} з операцією множення комплексних чисел. Маємо i i = -1. Як бачимо добуток двох елементів множини A не належить до цієї множини. Інакше кажучи, множина A не замкнена відносно визначеної в групі G операції. Якщо тепер розглядати множину A у відриві від групи, але з операцією, яка була визначена в групі, то не для всіх пар елементів цієї множини існує добуток.
Розглянемо ще підмножину B = { 1, 2, …, 2 n, …} групи Q *. Тут групова операція не виходить за межі множини B, але всі елементи, крім 1, не мають обернених у цій множині.
Переконаємося в справедливості такого критерію: підмножина Н групи G є підгрупою, тоді і лише тоді, коли:
а) для всіх h1, h2 Î H: h1 h2 Î H;
б) для всіх h Î H: h- 1Î H.
Дійсно, умова а) дозволяє ввести на множині Н ту саму операцію, яка була в групі. Зрозуміло, що ця операція є асоціативною. Умова б) гарантує існування обернених елементів в Н. Нарешті, з умов а) і б) випливає, що нейтральний елемент групи належить до Н: якщо h Î H, то h- 1Î H і тоді h h- 1= е Î H.
Далі наведено приклади підгруп:
1) кожна група G має дві так звані тривіальні підгрупи {е} і G;
2) в ланцюгу Z Ì Q Ì R Ì C кожна попередня група є підгрупою наступної;
3) група Cn є підгрупою групи C*. Отже, нескінченна група може мати скінченні підгрупи;
4) множина всіх парних підстановок n елементів є підгрупою групи Sn. У той же час множина всіх непарних підстановок не утворює підгрупу;
5) множина всіх матриць, визначник яких рівний ±1, є підгрупою групи GLn(C).
Елемент g групи G називається елементом скінченого порядку, якщо існує таке натуральне n, що gn = e. Найменше натуральне число з такою властивістю називається порядком елемента g і позначається через O(g).
Наприклад, у групі C*, O(i) =4, O(cos( 2 p / 5 )+ i sin( 2 p / 5 )) = 5,елемент 2 має нескінченний порядок.
Група, в якій кожний елемент має скінчений порядок, називається періодичною.
Розглянемо всі степені (додатні та від’ємні) фіксованого елемента g групи G: e, g, g 2, …, g- 1, g- 2, …. Зрозуміло, що ця множина є підгрупою групи G. Вона називається циклічною підгрупою, а елемент – її твірним елементом.
Далі наведено приклади циклічних підгруп:
1) множина C 4 = {i, i 2=-1, i 3= -i, i 4=1 } – циклічна підгрупа групи C* з твірним елементом i;
2) нехай a Î S 3є підстановкою a = ( 1, 2 ). Тоді a 2= e, a 3= e, a 4= e і т.д ., a- 1= a. Отже, множина {e, a} є циклічною підгрупою групи S 3;
3) матриця 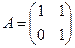 породжує циклічну підгрупу групи GL 2 (C). Легко перевірити, що
породжує циклічну підгрупу групи GL 2 (C). Легко перевірити, що 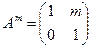 , m Î Z. Маємо приклад нескінченної циклічної підгрупи.
, m Î Z. Маємо приклад нескінченної циклічної підгрупи.
Група G називається циклічною, якщо знайдеться такий елемент g Î G, що породжена ним циклічна підгрупа співпадає з G.
Прикладами скінченних циклічних груп є групи Cn i Zn. Група Z відносно додавання є нескінченною циклічно групою з твірним елементом 1 (степенем елемента тут є його кратне). Зрозуміло, що будь-яка циклічна група є абелевою.
Нехай Н – підгрупа групи G, g – фіксований елемент у G. Лівим суміжним класом групи G за підгрупою Н (з представником g) називається множина елементів вигляду gh, де h пробігає всі елементи підгрупи Н; цю множину позначатимемо через gH. Аналогічно визначається правий суміжний клас групи G за підгрупою Н.
Далі наведено приклади суміжних класів:
1) нехай G = S 3 – група парних підстановок з 3 елементів. Позначимо елементи групи S 3так: e = 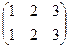 , a =
, a = 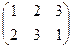 , b =
, b = 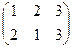 , c =
, c = 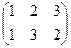 , d =
, d = 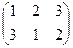 , a 2 =
, a 2 = 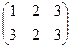 .
.
H = { e, a, a 2} – підгрупа парних підстановок групи S 3.
Таблиця Келі виконання операції композиції підстановок для групи S 3 виглядає так:
| ◦ | e | a | b | c | d | a 2 |
| e | e | a | b | c | d | a 2 |
| a | a | a 2 | d | b | c | e |
| b | b | c | e | a 2 | d | |
| c | c | d | a 2 | e | a | b |
| d | d | b | a | a 2 | e | c |
| a 2 | a 2 | e | c | d | b | a |
Ліві суміжні класи за підгрупою H:
eH ={ e, a, a 2}, aH ={ e, a, a 2}, a 2 H ={ e, a, a 2},
bH ={ b, c, d }, cH ={ b, c, d }, dH ={ b, c, d }.
Праві суміжні класи за підгрупою H:
He ={ e, a, a 2}, Ha ={ e, a, a 2}, Ha 2={ e, a, a 2},
Hb ={ b, c, d }, Hc ={ b, c, d }, Hd ={ b, c, d }.
Як бачимо, у даному прикладі eH = He, aH = Ha, bH = Hb, cH = Hc, dH = Hd, a 2 H = Ha 2, тобто ліві суміжні класи співпадають з відповідними правими суміжними класами.
Проте таке співпадіння не завжди має місце, як показує такий приклад:
2) нехай G = S 3, H = {e, b}. Лівий суміжний клас, породжений елементом d, складається з двох елементів: dH = {de, db} = {d, a}. Правий суміжний клас Hd = {ed, bd} = {d, a 2 }. Як бачимо, в цьому випадку dH ¹ Hd;
3) нехай G = Z, H – підгрупа цілих чисел, кратних числу 5. Суміжний клас, утворений числом 1, є множиною 1 + 5 Z = { 1, 1±5, 1±2·5, … }. Це всі цілі числа, які при діленні на 5 дають остачу 1.
Очевидно, що існує тільки 5 різних класів групи Z за підгрупою 5 Z: 5 Z, 1 + 5 Z, 2 + 5 Z, 3 + 5 Z,4 + 5 Z.
Зафіксуємо деяку підгрупу H групи G і розглянемо всі можливі ліві суміжні класи за цією підгрупою, утворені елементами групи G. Перш за все ясно, що кожний елемент g Î G належить до деякого класу, а саме, до класу gH, бо g = ge Î gH.
Далі, якщо підгрупа H скінченна і має n елементів, то кожен суміжний клас також має n елементів. Дійсно, якщо h 1 ¹ h 2, то gh 1 ¹ gh 2, бо за законом скорочення із gh 1 = gh 2 отримуємо h 1 = h2.
Для нескінченної підгрупи ці міркування означають, що множини gH та H рівнопотужні. Тоді й ліві суміжні класи рівнопотужні.
Усе раніше сказане справедливе й для правих суміжних класів.
Лема. Усякі два суміжні класи або не перетинаються або співпадають.
Доведення. Треба довести: із g 1 H Ç g 2 H ¹ Æвипливає g 1 H = g 2 H. Нехай g 0 Î g 1 H Ç g 2 H, тобто g 0 = g 1 h 1 = g 2 h 2, де h 1, h 2 Î H. Тоді g 1 H Í g 2 H. Це випливає з низки рівностей: для будь-якого h Î H: g 1 h = g 1 (h 1 (h 1 )- 1 )h = g 0 h ' = g 2 h 2 h ' = g 2 h '' Î g 2 H.
Аналогічно можна довести, що g 2 H Í g 1 H.
Теорема Лагранжа. Порядок будь-якої підгрупи H скінченої групи G є дільником порядку групи.
Доведення. Кожен елемент g Î G належить принаймні до одного класу, а саме до класу gH. Тому суміжні класи утворюють покриття групи. За доведеною лемою бачимо, що група є об’єднанням суміжних класів, які не перетинаються. Число класів позначатимемо через j і назвемо індексом підгрупи H у групі G. Оскільки всі класи мають однакове число елементів, то n = j m, де n – порядок групи G; m – порядок підгрупи H. Теорему доведено.
Наслідок. Група простого порядку не має жодних підгруп, крім тривіальних. Порядок елемента скінченої групи ділить порядок групи. Група простого порядку завжди циклічна.
Не слід думати, що для будь-якого дільника m порядку групи завжди існує підгрупа порядку n. Так, у групі A 4 (парні підстановки в S 4) порядку 12 не існує підгруп порядку 6.
Підгрупа Н групи G називається нормальною підгрупою, якщо gH = Hg для всіх g Î G. Остання умова означає, що відповідні ліві й праві суміжні класи за нормальною підгрупою співпадають. Сукупність суміжних класів за нормальною підгрупою утворює групу. Операція множення суміжних класів визначається за допомогою рівності g 1 H•g 2 H = (g 1 g2)H. Ця група називається фактор-групою групи G за нормальною підгрупою Н і позначається G / Н.
Відображення f: G 1 ® G2 групи (G 1, •) в групу (G 2, *) називається гомоморфізмом, якщо для будь-яких елементів x, y Î G 1, f(x • y) = f(x) * f(y).
Розглянемо два приклади.
а) C 2 = { -1, 1 } – група квадратних коренів з одиниці. Групова операція визначається рівностями 1·1 = 1, 1·(-1) = (-1)·1 = -1, (-1)·(-1) = 1.
б) S 2 – група підстановок другого порядку. Елементами є підстановки e = ( 1 ), a = ( 1, 2 ). Тут ee = e, ea = ae = a, aa = e.
Розглянемо тепер довільну групу другого порядку, абстрагуючись від природи її елементів. Вона мусить мати нейтральний елемент e і ще один елемент a, відмінний від нейтрального. Групова операція задається наступною таблицею Келі:
| Т | е | а |
| е | е | а |
| а | а | е |
Це єдино можливий варіант таблиці. Дійсно, рівності еТе = е, еТа = аТе = а випливають із визначення нейтрального елемента. Рівність аТа неможлива, бо це означало б, що а – нейтральний елемент. Значить, аТа = е.
Групи C 2і S 2 мають таку саму таблицю; в першому випадку треба замінити e i a на 1 і –1. Зауважимо, що ці групи є циклічними, а тому й абелевими.
Отже, з точки зору побудови закону композиції всі групи другого порядку не відрізняються між собою. Це можна виразити ще так. Нехай (G 1, •) = {e 1, a1}, (G 2, * ) = {e 2, a 2 } – дві групи. Існує бієктивне відображення f: G 1 ® G 2, визначене рівностями f(e 1 ) = e 2, f(a 1 ) = a 2, при якому зберігаються закони композиції. Це означає, що f(e 1 • a 1 ) = f(e 1 ) * f(a 1 ), f(а 1 • a 1 ) = f(а 1 ) * f(a 1 ). Справді, f(e 1 • a 1 ) = a 2 та f(а 1 • a 1 ) = e 2, f(e 1 ) * f(a 1 ) = e 2 * a 2 = a 2 та f(а 1 ) * f(a 1 ) = a 2 * a 2 = e 2.
Слід зауважити, що друге можливе тут відображення g: G 1 ® G 2, визначене рівностями g(e 1 ) = а 2, g(a 1 ) = е 2, не зберігає законів композиції. Це видно з наступного: g(а 1 • a 1 ) = a 2та g(а 1 ) * g(a 1 ) = e 2 * e 2 = e2. Отже, g(а 1 • a 1 ) ¹ g(а 1 ) * g(a 1 ).
Бієктивне відображення f: G 1 ® G 2групи (G1, •) в групу (G 2, *) називається ізоморфізмом, якщо для будь-яких елементів x, y Î G 1, f(x • y) = f(x) * f(y).
Іншими словами, ізоморфізмом з групи G 1 в групу G2 називається бієктивний гомоморфізм з групи G 1 в групу G2 .
Дві групи G1 i G2 називаються ізоморфними, якщо існує ізоморфізм групи G 1в групу G 2; це позначають G 1 @ G 2.
Таким чином, нами встановлено, що всі групи другого порядку ізоморфні. Проте, як далі бачимо, існують неізоморфні групи, навіть якщо існує бієктивне відображення однієї групи на іншу.
Групи Q+ додатних раціональних чисел відносно множення й Q раціональних чисел відносно додавання неізоморфні. Правда, існують бієктивні відображення множини Q+ на множину Q, але жодне з них не може бути ізоморфізмом. Справді, яке б не було бієктивне відображення f: Q+ ® Q, завжди існують такі елементи а Î Q і х Î Q+, що f( 2 ) = а і f(х) = а/ 2. Якби це відображення було ізоморфізмом, то повинно бути f(х 2 ) = а/ 2 + а/ 2 = а = f( 2 ). Звідси за бієктивністю відображення х 2 = 2, що неможливо, бо х - додатнє раціональне число.
Дві скінченні ізоморфні групи мають однакові таблиці Келі в такому розумінні: якщо всі елементи аі в першій таблиці замінити відповідно на f(аі) (f - ізоморфізм груп), то отримаємо другу таблицю.
Покажемо, що існує лише одна таблиця для групи третього порядку G={e, a, b}. Перший рядок та перший стовпець таблиці мусять мати вигляд: e, a, b. Як можна заповнити порожні місця? Зауважимо, що в кожному рядку й у кожному стовпці повинні бути всі елементи без повторень незалежно від порядку групи. Дійсно, коли б ai aj = ak і as aj = ak, то було б ai aj=as aj. Звідси за законом скорочення ai = as (при i ¹ s), що неможливо.
Чому може дорівнювати а 2? Це не може бути е, бо в другому рядку на останньому місці доведеться ставити b. Але b вже є в третьому стовпці. Залишається тільки варіант а 2 = b. Тепер легко заповнити всю таблицю.
| Т | е | а | b |
| е | е | а | b |
| а | а | b | е |
| b | b | е | а |
Треба ще довести, що бінарна алгебраїчна операція, задана цією таблицею, асоціативна. Це можна зробити обхідним шляхом. Відомо, що існують групи третього порядку (група C 3 і підгрупа парних підстановок групи S 3) з такою ж таблицею.
Таким чином, з точністю до ізоморфізму існує лише одна група третього порядку, яка, як видно з таблиці, є абелевою. Інакше кажучи, всі групи третього порядку ізоморфні між собою.
Збудуємо таблицю Келі операції для циклічної групи четвертого порядку за рівностями a 2 = b, a 3 = c, a 4 = e.
| Т | е | а | b | c |
| е | е | а | b | c |
| а | а | b | c | e |
| b | b | c | e | a |
| c | c | e | a | b |
Виникає запитання: чи існують нециклічні групи четвертого порядку? Слід зауважити, що за теоремою Лагранжа всі її елементи повинні мати порядок 2, тобто a2 = b 2 = c 2 = е Далі показано, як заповнити (це можна зробити єдиним способом) таблицю Келі для цього випадку
| Т | е | а | b | c |
| е | е | а | b | c |
| а | а | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
| Т | е | а | b | c |
| е | е | а | b | c |
| а | а | e | ||
| b | b | e | ||
| c | c | e |
Легко перевірити, що таку таблицю має група підстановок множини з чотирьох елементів a = ( 1, 2 )( 3, 4 ), b = ( 1, 3 )( 2, 4 ), c = ( 1, 4 )( 2, 3 ), e = ( 1 ). Ця група є абелевою, бо таблиця Келі симетрична відносно головної діагоналі. Це так звана група Клейна.
Отже, з точністю до ізоморфізму існує лише дві групи четвертого порядку.
Теорема Келі. Будь-яка група G ізоморфна деякій підгрупігрупи Aut(G).
Наслідок. Якщо G – скінченна група порядку n, то вона ізоморфна деякій підгрупі групи підстановок Sn.
Таким чином, вивчення скінчених груп можна звести до вивчення груп підстановок.
Нехай К – непорожня множина, на якій задані дві бінарні алгебраїчні операції + (додавання) і ∙ (множення), які задовольняють наступним умовам:
(K1) (K, +) – абелева група;
(К2) (K, ∙) – півгрупа;
(К3) операція множення дистрибутивна відносно операції додавання:
(x + y) z = x z + y z, z (x + y) = z x + z y
для всіх x, y, z Î K.
Тоді (K, +, ∙) називається кільцем.
Структура (K, +) називається адитивною групою кільця, а (K, ∙) - його мультиплікативною півгрупою.
Якщо (K, ·) – моноїд, то кажуть, що (K, +) – кільце з одиницею. Кільце називається комутативним, якщо (K, ∙) – абелева півгрупа (на відміну від груп, комутативне кільце не прийнято називати абелевим). Нейтральний елемент 0 – відносно додавання і 1 – відносно множення (якщо він існує) називають відповідно нулем і одиницею кільця.
Далі наведено приклади кілець:
1) множина (Z, +, ∙) цілих чисел відносно звичайних операцій додавання й множення;
2) множина (Q, +, ∙) раціональних чисел відносно звичайних операцій додавання й множення;
3) множина (R, +, ∙) дійсних чисел відносно звичайних операцій додавання й множення;
4) множина (C, +, ∙) комплексних чисел відносно звичайних операцій додавання й множення;
5) множина дійснозначних матриць Мn(R) розміру n x n відносно додавання та множення матриць є кільцем з одиницею. Роль нейтрального елемента відносно множення тут відіграє одинична матриця Е. Таке кільце називається повним матричним кільцем над R або кільцем квадратних матриць порядку n над R. Це один з найважливіших прикладів кілець. Оскільки при n > 1, матриці при множенні, як правило не можна переставляти, то Мn(R) – некомутативне кільце.
Підмножина L кільця К називається підкільцем, якщо для будь-яких елементів x, y Î L
x + y Î L i x ∙ y Î L.
Підкільце L кільця К з одиницею називається ідеалом, коли для будь-яких елементів x Î L та a Î K виконується a ∙ x Î L, x ∙ a Î L.
Нехай К - кільце з одиницею, а L – ідеал у цьому кільці. Фактор-групу К / L адитивної групи (K, +) кільця за ідеалом L (який є нормальним дільником в адитивній групі) можна перетворити в кільце, наступним чином задаючи операцію множення суміжних класів: (x + L) · (y + L) = x ∙ y + L. Це кільце називається фактор-кільцем кільця К за ідеалом L і позначається К / L.
Нижче наведено приклад фактор-кільця, який широко використовується. Множина nZ цілих чисел, кратних деякому фіксованому натуральному числу n, є ідеалом в кільці цілих чисел Z. Розглянуту раніше фактор-групу Z / nZ = Zn можна перетворити в кільце задаючи операцію множення Ä класів за модулем числа n. Щоб перемножити два класи 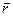 і
і 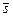 потрібно спочатку перемножити цілі числа r і s, а потім знайти остачу від ділення знайденого добутку на число n. Клас знайденої остачі й буде результатом множення класів
потрібно спочатку перемножити цілі числа r і s, а потім знайти остачу від ділення знайденого добутку на число n. Клас знайденої остачі й буде результатом множення класів 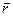 і
і 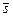 . Множина Zn разом із заданими на ній операціями додавання Å та множення Ä є комутативним кільцем з одиницею, яке має n елементів.
. Множина Zn разом із заданими на ній операціями додавання Å та множення Ä є комутативним кільцем з одиницею, яке має n елементів.
Далі наведено таблицю Келі для операції множення Ä кільця Z 5:
| Ä | 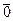
| 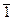
| 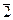
| 
| 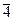
|
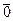
| 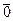
| 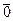
| 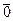
| 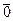
| 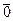
|
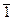
| 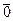
| 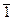
| 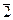
| 
| 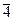
|
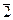
| 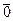
| 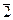
| 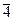
| 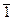
| 
|

| 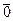
| 
| 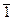
| 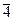
| 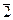
|
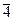
| 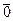
| 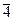
| 
| 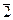
| 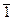
|
Відображення f: К 1 ® К 2 кільця (К 1, +, ∙) в кільце (К 2, Å, Ä) називається гомоморфізмом, якщо воно зберігає всі операції, тобто коли для будь-яких елементів x, y Î К 1
f (x + y) = f (x) Å f (y),
f (x ∙ y) = f (x) Ä f (y).
Якщо гомоморфізм кілець є бієктивним відображенням, то він називається ізоморфізмом кілець. Два кільця К 1 i К 2 називаються ізоморфними, якщо існує ізоморфізм кільця К 1 в кільце К 2; факт ізоморфізму кілець коротко записують у вигляді К 1 @ К 2.
Поле Р – це комутативне кільце з одиницею, в якому кожен відмінний від нуля елемент має обернений відносно операції множення. Іншими словами комутативне кільце з одиницею Р є полем, коли сукупність його відмінних від нуля елементів утворює абелеву групу відносно операції множення.
Два поля Р 1 i Р 2 називаються ізоморфними, якщо вони ізоморфні як кільця.
Поле, яке має скінченне число елементів, називається скінченним полем або полем Галуа.
Теорема. Будь-яке скінченне поле має рn елементів, де р – просте, а n – натуральне число. Для фіксованих простого числа р і натурального числа n існує і, з точністю до ізоморфізму, лише одне поле з числом елементів рn.
Скінченні поля з точністю до ізоморфізму будуються наступним чином.
Скінченне поле з р елементів ізоморфне кільцю Zp цілих чисел за модулем р.
Скінченне поле з рn елементів отримується таким чином. Розглядаємо кільце многочленів Zp[x] від змінної х над полем Zp. Беремо в цьому кільці многочлен f(x) степеня n, який є нерозкладним над Zp. Позначаємо через (f(x)) ідеал, який складається з елементів, що діляться на f(x). Тоді фактор-кільце Zp[x] / (f(x)) є бажаним полем з рn елементів. Виконання операцій над елементами цього поля здійснюється за двома модулями: за модулем числа р і за модулем многочлена f(x). Часто це позначається наступним чином: (mod f(x), p).
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 2555; Нарушение авторских прав?; Мы поможем в написании вашей работы!