ДОДАТКОВО 1 страница

Для спрощення проміжних розрахунків використаємо вбудовану в електронні таблиці Microsoft Excel статистичну функцію ЛИНЕЙН. Ця функція застосовує метод найменших квадратів, щоб визначити оцінки параметрівлінійної регресії.

ЛИНЕЙН (відомі_значення_Y; відомі_значення_Х; конст; ста­тистика).

Результат – це оцінка параметрів лінійної регресії та регресійна статистика.

Для цього треба:

1) відмітити поле, де буде знаходитись результат розміром (k + 1) ´ 5, або m₁ ´ 5; m₁ = k + 1

2) ввійти у "майстер функцій f ". У категоріях вибираємо "статистична", а в функціях – ЛИНЕЙН. Вводимо адреси значень Y, Х та значення константи і статистики;

3) для того, щоб отримати на екрані результат, натискаємо спершу клавішу F2, а потім Ctrl+Shift+Еnter.

Функція може додатково обчислювати регресійну статистику (рис.1.1).

«Відомі значення Y» — множина значень Y. Якщо масив Y має один стовпець, то кожний стовпець масиву «відомі_значення_Х» інтерпретуються як окрема змінна. Якщо масив «відомі_значення_Y» має один рядок, то кожний рядок «відомих значень Х» інтерпретується як окрема змінна.

«Відомі_значення_Х» — множина значень Х, що враховує або одну (парна регресія), або кілька змінних (множинна регресія). Якщо «відомі_значення_Х» пропустили, то вважається, що це ма­сив {1; 2; 3;...} такого самого розміру, як n «відомих_значень Y».

«Конст» — логічне значення.

Якщо «конст» має значення «ложь», то a ₀ беруть таким, що дорівнює нулю: значення aдоби­рають так, щоб виконувалася рівність Y = ХА (модель без вільно­го члена).

Якщо «конст» має значення «истина», то a ₀ обчислює­ться традиційно (модель з вільним членом).

«Статистика» — логічне значення, яке вказує, чи потрібно об­числювати додаткову статистику за регресією.

Якщо «статисти­ка» має значення «истина», то функція ЛИНЕЙН обчислює до­даткову регресійну статистику у вигляді масиву (див. рис. 1.1).

		…
		…
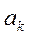
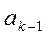
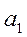
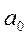
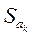
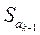
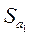
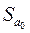
R^2
F	Ступінь свободи n–m

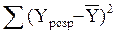
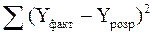
Рис. 1.1. Статистика функції ЛИНЕЙН

де 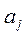– оцінка параметра 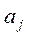, j=1..k;

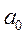– оцінка вільного члена регресії;

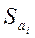– стандартна похибка оцінки параметра a_і;

R² – коефіцієнт детермінації;

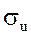– стандартна похибка залишків;

F – F-критерій.

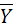– середнє значення Y_факт.

Ступінь свободи дорівнює (n – m), де n – кількість спостере­жень, m – кількість змінних у моделі; це значення необхідне для визначення табличного значення F-критерію.

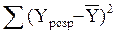–сума квадратів відхилення, що пояснюється регресією;

– сума квадратів відхилення, що пояснюється по­хибкою u.

Якщо статистика має значення «ложь» чи її пропустили, то функція ЛИНЕЙН обчислює лише коефіцієнти a_j та константу a₀.

Лабораторна робота № 1. «Лінійна модель»

Згідно з вибіркою статистичних даних побудувати лінійну модель залежності Y від X виду: .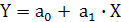

Мета роботи:

визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 1

Варіант 1		Варіант 2		Варіант 3		Варіант 4		Варіант 5
Y	Х		Y	Х		Y	Х		Y	Х		Y	Х
12,3	9,6		16,1	12,2		12,7	12,4		15,8	12,3		16,9	19,3
14,7	8,1		16,3			12,9	10,3		19,4			17,7	18,7
15,8	6,3		17,8	8,1		13,3	10,1		20,3	6,1		18,3	8,9
16,3	5,5		17,6			14,7	8,4		27,8	6,2		18,4	6,3
17,1	4,1		18,5	7,6		16,9	6,3		29,3	5,1		19,7
20,9	2,8		18,9	7,4		20,1	6,2		24,4	4,3		20,8	5,5
21,4	1,6		20,1	6,1		23,4	5,4		31,3	3,8		21,3
22,8	0,9		24,3	5,3		24,5	5,3		32,8			22,9	2,9
23,9	0,8		25,8	2,7		28,4			32,9	2,7		25,4	1,3
24,1	0,4		26,7	2,6		30,7	4,8		34,7	2,5		26,9	0,7
Варіант 6		Варіант 7		Варіант 8		Варіант 9		Варіант 10
Y	Х		Y	Х		Y	Х		Y	Х		Y	Х
10,9	12,4		16,3	10,3		16,7	15,1		15,9	6,3		12,8	6,3
11,3	10,1		16,7	8,1		17,3			16,1			12,9	5,1
12,8	8,4		18,1	6,4		18,4	12,4		17,4	6,1		13,1
13,8			18,9			19,5	9,3		18,3	5,5		14,4	4,2
14,9	7,9		19,3	4,1		20,3	8,6		18,9			15,8	3,3
15,6	5,4		20,4	3,3		21,4	5,1		20,4	4,3		16,3	2,1
18,1	6,1		21,5	3,3		25,5	3,3		21,3			17,9
19,4	3,1		24,6	2,7		26,9	3,2		22,8			18,1	1,9
			27,8	2,1		27,8			23,4	3,5		19,3	1,7
21,3	2,1		27,9	0,9		30,1	2,1		25,7	3,1		20,4	1,1
Варіант 11		Варіант 12		Варіант 13		Варіант 14		Варіант 15
Y	Х		Y	Х		Y	Х		Y	Х		Y	Х
10,4	12,7		10,7	9,1		15,6	12,3		12,3	12,3		12,3	6,3
11,5	11,8		11,8	8,6		15,8	10,1		12,5	10,1		12,9
12,7	10,3		13,8	8,6		16,3	8,7		13,7	8,8		13,4
13,8	9,1		14,9			16,9	6,5		13,9	7,3		14,7	5,8
14,3			15,1	7,4		20,1	3,1		14,7	6,9		15,1	5,3
14,9	8,5		16,3	7,1		21,3			15,1	5,1		16,9	5,1
15,1	7,4		17,1	6,9		24,9	2,1		16,3			17,3
16,3			18,7	6,2		25,8	1,5		17,4	4,1		18,7	4,1
17,9	6,3		18,9	5,3		26,9	1,4		18,1	3,2		19,8	3,2
18,4	5,1		19,3	4,2		27,3	0,9		18,9	3,1		20,1	2,7
Варіант 16		Варіант 17		Варіант 18		Варіант 19		Варіант 20
Y	Х		Y	Х		Y	Х		Y	Х		Y	Х
10,3	6,7		15,1	10,7		12,7			20,8	5,1		6,9	10,1
10,9	6,5			8,1		12,8	9,1		21,9			10,3	9,4
11,7			15,6				8,7		21,9	4,9		12,5	6,5
12,8	5,9		15,9	6,7		13,9	8,8		23,4	4,9		12,4	5,1
13,9	4,1		16,1	6,6		14,1	8,6		25,7	3,1		13,7
14,7			16,3			15,8	7,1		26,8			16,8	4,2
15,1	3,8		17,8	6,5		16,1	6,3		27,1	2,8		19,3	3,1
16,9	2,7					17,3	5,1		28,1	2,1		20,1	2,8
21,9	1,9			5,1		18,9	4,2		30,3	1,8		21,7
18,7	0,8		18,4	4,3		18,9	2,8		31,4	0,9		25,8	1,9
Варіант 21		Варіант 22		Варіант 23		Варіант 24		Варіант 25
Y	Х		Y	Х		Y	Х		Y	Х		Y	Х
19,8	10,5		5,6	7,9		15,6	9,1		10,7	6,1		10,1	6,7
20,3	9,4		5,6	7,8		15,8							5,1
21,4	8,3		5,8	7,6		16,1	7,1		10,9			10,7	6,9
22,9	6,1		5,9	6,1		18,4			11,5	6,3		11,3	6,9
24,6	5,4		6,7				6,8		11,9	5,8		11,8	5,4
27,8	2,2		7,9	5,8		19,1	6,3			5,7		12,4	7,1
29,3			8,3	5,5		20,3	6,3					15,7	6,3
30,1	1,9		8,7	5,4		21,7			13,7	5,4		15,8	6,5
33,4	0,7		10,1	4,1		29,8	6,1		14,1	5,1		16,1	6,1
35,8	0,6		15,4			30,3	5,8		14,8				5,8
Варіант 26		Варіант 27		Варіант 28		Варіант 29		Варіант 30
Y	Х		Y	Х		Y	Х		Y	Х		Y	Х
12,9	3,3		15,4	7,7		19,1	7,3		18,1	4,5		13,1	8,3
			15,6			19,3						13,4
12,7	3,1		16,1	7,9			7,1		17,6	4,1			8,7
13,4	3,1		17,3	7,1		19,4	6,9		18,4	4,6		12,8	8,1
14,7	2,8		17,5	6,8		20,5	6,5		19,1	3,7		14,5	7,5
15,1	2,5		18,1	5,3		21,6	5,5		19,9	3,1		14,8	6,5
15,8	2,3		18,6	5,1		22,8	5,7		20,1			15,1
16,3	2,1		18,9	4,2		23,7			20,3	2,8		15,4	5,9
17,4			20,3			24,1	4,1		21,4	2,5		15,9	5,4
18,1	1,5		21,4	1,9		25,6	3,1		22,5			16,3	5,1

Лабораторна робота № 2. «Степенева функція»

Згідно з вибіркою статистичних даних побудувати степеневу модель залежності Y від X виду: .

Мета роботи:

визначити аналітичну залежність між дослідними даними із застосуванням методу найменших квадратів (знайти параметри моделі);

представити модель на графіку (графічне відображення моделі засновується на побудові лінії тренду в прямокутних координатах Y-X).

Похідні дані для розрахунку моделей лабораторної роботи № 2

Варіант 1		Варіант 2		Варіант 3		Варіант 4		Варіант 5		Варіант 6
Y	X		Y	X		Y	X		Y	X		Y	X		Y	X
30,4	50,5		19,3	20,5			80,5		30,5	20,1		30,1	50,3		60,1	80,3
31,5	50,7		19,5	20,7			80,4			20,4		30,3	49,8		60,2	80,4
31,6	50,8		19,8	21,3			80,3		27,7	21,9		30,4	48,7			81,7
39,7	59,3		19,9	22,4		68,1	80,1		27,6	28,8		30,5	45,5		60,1	82,8
38,8	60,1			22,7		68,2	78,9		27,6	29,5		30,7			60,3	82,9
40,5	70,3					68,3	78,5			29,6		31,8	42,1		60,4	85,1
42,7			23,1	29,1		68,4	78,2		25,5	29,8		32,1	40,3		60,5	87,1
49,9	75,5		24,7	30,3		68,5	78,1		21,6	30,4		33,4	38,4		61,6	88,3
50,1	76,6		28,4	31,4		68,6			21,3	30,7		35,5	35,3		62,7	89,4
50,2	77,8		29,3			68,7	76,7		21,3	30,9		36,6	30,3		63,8	90,5
53,3	79,8		29,5			68,8	75,6		21,1	35,4			30,1		64,7	91,6
55,7	79,9		29,9	34,1		68,8	74,4		20,9	37,1		28,8	28,3		65,5
60,1			30,1	35,6		68,9	73,1		20,2	39,5		29,9	27,6		66,7	92,3
75,5			31,3	37,8		69,9	72,8		20,1	40,2		20,1	25,5		68,1	93,7
81,3	93,3		32,4	39,5		70,1	70,7		19,9	46,8		20,2			69,7	94,5
Варіант 7		Варіант 8		Варіант 9		Варіант 10		Варіант 11		Варіант 12
Y	X		Y	X		Y	X		Y	X		Y	X		Y	X
82,3	99,9		19,1	20,5		44,1	50,5		30,5	46,6		65,5	70,6			59,1
82,5	98,7		19,2	20,7			50,6			40,5			70,7		48,8
88,6	97,6		19,3	21,3		43,9	50,7		27,7	39,1			70,8		47,7	55,7
	96,6			22,7		43,8	50,8		27,6	37,1		61,8	70,9		44,3
	95,5		20,1	22,4		43,7	51,1			35,5		62,1	72,3		42,7	50,2
				22,5		43,6	52,2		26,6	30,9		57,8	72,4		41,7	50,1
89,4			21,1				53,4		25,5	30,7		55,2	72,5		39,3	49,3
89,5	93,5			25,1		41,1	55,5		22,4	30,1		43,9	72,9		38,8	48,1
89,7	93,1			24,1					21,6	29,7		42,5	80,1		30,7	47,7
90,1				25,6					21,5	29,4			85,5		29,3	46,7
90,2				27,1			60,1		21,3	29,3		38,8			29,1	44,5
90,3			24,4	27,9		39,8			20,1	28,8		35,9	88,1		28,3	41,3
92,1	90,3		25,5	28,1		39,7			20,1	21,7		32,4	89,3		27,4	30,9
92,3	90,1		26,1	29,3		39,6	65,5			20,5		31,2	90,1		26,5	30,8
93,3			27,3	29,5		39,6	66,6		19,7	20,3		30,7	90,2		25,5	30,7
Варіант 13		Варіант 14		Варіант 15		Варіант 16		Варіант 17		Варіант 18
Y	X		Y	X		Y	X		Y	X		Y	X		Y	X
	50,3		61,7						30,1	40,1			39,7		30,4	64,3
	50,7		60,3	81,7		24,1	50,1		29,4	42,3		28,8	41,6		35,5	68,7
45,1	51,3			89,1		24,1	48,9		31,3	44,1		31,3	42,4		37,8	70,1
45,2			61,8	89,4		24,3				45,8		32,4	43,5		38,9	75,5
45,4	55,1		60,1	80,5		24,5	45,5		28,3	49,7		27,9	46,6		40,1
45,5	56,3		59,8	80,3		24,7	40,5		27,8	50,3		26,3	47,7		47,7	80,3
45,5	57,1		62,3	90,1		24,8	39,9		32,7	55,8		33,7	48,9		48,9	81,8
	58,3		63,4	90,3		24,9	39,1		33,8	56,9		35,8	50,1		49,9	82,9
46,1			63,9	91,7		25,1			34,7	60,3		39,6	52,3		50,1
46,7	59,1		64,5	91,9		25,3			35,9	61,9					52,3	85,1
47,1	59,3		65,6			25,6			38,1	68,8		41,2	57,9			86,9
47,8	60,3		66,7	96,1		25,7	33,1		44,1	70,4		42,3	60,1		55,6	90,3
47,9	61,7		67,8	97,1		25,8	31,3		45,3	71,7		43,3	64,3		57,8	91,4
48,1			68,8	97,8					48,8	78,8		45,6	65,9		59,3	92,2
			69,9	99,1			30,9		49,1	79,3		47,8	66,7		60,1	93,3
Варіант 19		Варіант 20		Варіант 21		Варіант 22		Варіант 23		Варіант 24
Y	X		Y	X		Y	X		Y	X		Y	X		Y	X
40,3	67,1		26,3	59,6		30,1	50,5		19,1	20,2		35,1	22,6		25,1	25,2
45,7	70,4		27,8	60,3		31,2	50,7		19,4	20,7		34,5	22,9		25,2	25,5
46,8	80,1			65,6		31,3	50,8		19,8	21,5		34,9	23,1		28,8	27,6
47,9	85,5		30,1	66,8		39,1	59,2		19,9	22,4		34,9	26,5		29,9	28,9
48,8	86,6		31,2	70,1		38,5	60,1		21,9	22,7		36,8	27,7			30,1
49,4	86,7		33,4			40,1	70,5		22,7			37,7	29,4		30,4	30,8
50,1				76,3		42,8			23,1	29,1		38,2	29,5		30,5	35,3
50,9	89,1			77,9		49,9	75,5		24,6	30,3		44,3	30,8		30,6	38,4
60,3	90,3		37,1	78,4		50,1	76,5		27,4	31,4		48,1	31,1		30,7	40,3
65,3	91,4		38,4	79,3		50,2	77,7		28,3	32,4		51,5	31,2		30,9	42,7
66,4	92,5		39,1	80,1		53,3	79,8		29,5	33,5		52,5	31,6		31,8
69,5	93,6		40,5	81,5		55,1	79,9		29,9	34,2		52,3	31,8		32,1	45,5
70,5	94,7		46,6	86,6		60,1			30,1	35,6		52,5			33,4	48,7
70,9	98,1		47,8	90,4		75,3			31,3	37,8		53,6	34,4		35,5	49,8
	98,2		50,1	95,6		81,3	93,5		32,4			55,8	35,4		36,6
Варіант 25		Варіант 26		Варіант 27		Варіант 28		Варіант 29		Варіант 30
Y	X		Y	X		Y	X		Y	X		Y	X		Y	X
81,3	93,3		32,4	39,5			80,5		30,5	46,8		20,1			69,7	94,5
75,5			31,3	37,8			80,4		27,6	40,2		20,2	25,5		68,1	93,7
60,1			30,1	35,6			80,3		25,5	39,5		28,8	27,6		66,7	92,3
55,7	79,9		29,9	34,1		68,1	80,1		27,6	37,1		29,9	28,3		65,5
53,3	79,8		29,5			68,2	78,9		27,7	35,4			30,1		64,7	91,6
50,2	77,8		29,3			68,3	78,5			30,9		30,1	30,3		63,8	90,5
50,1	76,6		28,4	31,4		68,4	78,2			30,7		30,3	35,3		62,7	89,4
49,9	75,5		24,7	30,3		68,5	78,1		21,6	30,4		30,4	38,4		61,6	88,3
42,7			23,1	29,1		68,6			21,3	29,8		30,5	40,3		60,5	87,1
40,5	70,3					68,7	76,7		21,3	29,6		30,7	42,1		60,4	85,1
39,7	59,3		19,9	22,4		68,8	74,4		20,9	28,8		31,8			60,1	82,8
38,8	60,1			22,7		68,8	75,6		21,1	29,5		32,1	45,5		60,3	82,9
31,6	50,8		19,8	21,3		68,9	73,1		20,2	21,9		33,4	48,7			81,7
31,5	50,7		19,5	20,7		69,9	72,8		20,1	20,4		35,5	49,8		60,2	80,4
30,4	50,5		19,3	20,5		70,1	70,7		19,9	20,1		36,6	50,3		60,1	80,3

Лабораторна робота № 3. «Параболічна функція»

Дата добавления: 2014-11-29