Ітерація 2

Ітерація 1

f 0		–9	–6
Базові невідомі	№ рядка	План (опорний розв'язок)	x1	x2	x3	x4	x5
x3			15
x4
x5

Критерій оптимальності. Якщо задача максимізується і в нульовому рядку відсутні від'ємні числа (за винятком хіба що сто­впчика "опорний розв'язок (план)"), то опорний план є оптималь­ним (при мінімізації задачі для оптимальності плану достатньо відсутності додатних чисел у нульовому рядку, за винятком, мож­ливо, опорного розв'язку).

Коефіцієнт рядка "0" можна інтерпретувати як приріст фун­кції f при збільшенні вільної невідомої на одиницю. Приріст буде додатним, якщо коефіцієнт від'ємний, і від'ємним – якщо коефіці­єнт додатний.

В нашому випадку є два від'ємні числа (–9), (–6), беремо най­більше за модулем від'ємне число (–9) (при мінімізації задачі – найбільше додатне), тоді стовпчик "х₁"будемо називати ключовим стовпчиком.

Для вибору ключового елемента складаємо відношення ві­льних членів (чисел стовпчика "опорний розв'язок") до відповід­них додатних чисел ключового стовпчика (усі інші відношення будемо вважати рівними нескінченності):

.

Перше відношення менше, тому число (15) першого рядка буде ключовим елементом. Ключовий елемент в таблиці позначаємо рамкою і переходимо до другої ітерації.

f 0
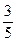
Базові невідомі	№ рядка	План (опорний розв'язок)	x1	x2	x3	x4	x5
х1
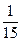
x4
x5

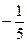
Послідовність заповнення другої та наступних ітерацій така (використовуємо метод Гаусса-Жордана):

1. Замість базової невідомої х₃ (ключовий рядок), вводимо
нову базову невідому х₁ (невідому ключового стовпчика),

2. Формально заповнюємо базові стовпчики (пункт 1 ітерації 1).

3. Ключовий рядок одержуємо від ділення його елементів
попередньої ітерації на ключовий елемент.

4. Усі інші комірки ітерації заповнюємо за правилом прямо­кутника:

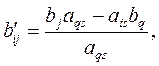(2.9)

де a_ij', b_i ' відповідно шукані елементи нової ітерації, а а_ij, b_i – попе­редньої,
а_qs – ключовий елемент.

Рядок 0: ; ; .

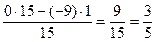Рядок 2: ; ; ; .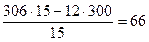

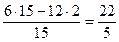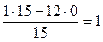Рядок 3: ; ; ;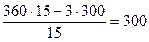

.

Після заповнення таблиці 2 - ої ітерації перевіряємо її опорний план на оптимальність. Бачимо, що потрібно перейти до на­ступного опорного плану, оскільки в нульовому рядку стовпчика "х₂" знаходиться від'ємне число ().

.

За ключовий елемент слід взяти число " ".

Дата добавления: 2014-11-29