Розв'язування

Приклад.

Для виготовлення двох видів продукції А і В використову­ють три види сировини: I, II та III.

На виробництво одинці продукції А знадобиться витратити:

сировини I виду – 15 кг,

сировини II виду – 12 кг,

сировини III виду – 3 кг.

На виробництво одинці продукції В знадобиться витратити:

сировини I виду – 2 кг,

сировини II виду – 6 кг,

сировини III виду – 12 кг.

Запаси сировини:

I виду – 300 кг,

II виду – 306 кг,

III виду – 360 кг

Прибуток від реалізації оди­ниці продукції виду А становить 9 грн.,
виду В – 6 грн.

Скласти план виробництва продукції, який забезпечить максимальний прибуток від реалізації при наявності даних запасів сировини.

Позначимо кількість виготовленої продукції першого виду А через х₁, другого – х₂. Враховуючи витрати сировини I, II та III виду на виготовлення одиниці продукції видів А та В, а також обмежені запаси сировини, запишемо систему обмежень (6.1). Прибуток, одержаний з виготовлення продукції у вигляді функції мети (6.2).

(2.6)

(2.7)

Зведемо задачу лінійного програмування (2.6, 2.7) до ка­нонічної форми додавши невідомі х₃, х₄ та х₅ до лівої сторони двох нерівностей відповідно:

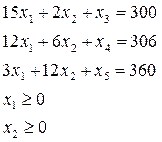(2.8)

;

.

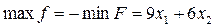Розв'яжемо систему рівнянь методом Гаусса-Джордана, то­му запишемо систему обмежень (2.8) у вигляді початкової розра­хункової таблиці, яку назвемо ітерацією 1.

Для знаходження початкового базового плану розділимо змінні на дві групи – базові і вільні. Для вибору базових змінних доцільно скористатися таким правилом: в якості базових змінних ітерації симплекс-таблиці необхідно вибрати такі змінні (їх кіль­кість визначається числом основних обмежень), кожна з яких тіль­ки раз входить у рівняння основних обмежень. Решту змінних бу­демо вважати вільними.

Запишемо цільову форму f у вигляді рівняння

Таблиця заповнюється формально за вибраною канонічною формою.

1. Заповнюємо базові стовпчики: на перетині однойменних ряд­ків і стовпчиків ставимо 1, а в усіх інших клітинках будуть нулі.

2. В інших рядках виписуємо коефіцієнти, що стоять біля відповідних невідомих. Нульовий рядок відповідає оптимізуючій формі і служить для визначення ступеня оптимальності опорного плану.

Дата добавления: 2014-11-29