ІІІ. Умови невід’ємності змінних

ІІ. Система обмежень.

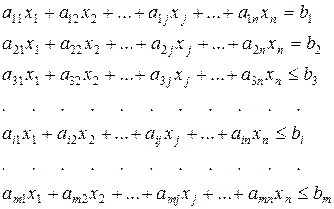(2.2.)

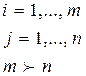
або: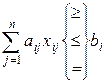

– коефіцієнти при невідомих змінних в рівняннях та тотожностях (можуть бути: норми витрат сировини, матеріалів на одиницю продукції; оптові ціни за одиницю продукції та ін.);

– невідомі змінні;

– рівень обмежень у рівняннях та тотожностях (рівень ресурсів: матеріальних, сировинних, трудових і т.д.).

На базі наведеного математичного опису можна проілюструвати суть цієї моделі так: необхідно визначити значення n невід’ємних змінних , які задовольняють обмеженням 2.2та забезпечують екстремальне значення (максимальне або мінімальне) цільової функції, яка виражена рівнянням 2.1.

До методів вирішення задач ЛП відносяться симплекс-метод, графічний метод.

Симплекс-метод є аналітичним методом знаходження рішення задач ЛП.

Як прави­ло, задачу зводять до канонічної форми. Вважають, що задача лінійного програмування записана в канонічній формі, якщо вона має вигляд

(2.3)

Щоб перевести задачу лінійного програмування з загальної форми (2.1–2.2) до канонічної форми (2.3) необхідно зро­бити такі кроки.

1-й крок. До кожної лівої частини нерівностей (2.2) додаємо нову невід'ємну невідому змінну х_п+і (i= 1,2,...,l–k), яка дорів­нює:

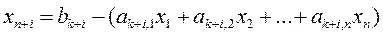
або:

Тоді група нерівностей(2.2)перетвориться на рів­няння.

Введені нові змінні, х_п+і,..., х_т–k будемо вважати базови­ми, а змінні
x₁,..., х_п – вільними.

Дістаємо однорідну систему основних обмежень задачі:

2-й крок полягає у зведенні до однорідної системи обмежень на знак. Умови недодатності легко перетворюються в умови невід'ємності за допомогою заміни змінних

Змінну, на знак якої не накладено обмежень, подають у ви­гляді різниці двох невід'ємних змінних:

Ранг сумісної системи обмежень (1.3) r можна вважати та­ким, що дорівнює т, оскільки в іншому разі частину, а саме т – r = k рівнянь треба було б відкинути, бо вони були б лінійними комбі­націями r базових рівнянь. Однак на практиці інколи такі зайві рі­вняння можуть включати в систему обмежень на стадії формуван­ня реальної задачі. Такі обмеження називають неістотними і їх відкидають, що звичайно відбувається при побудові довільного базового розв'язку системи рівнянь. Отже, знайти множину планів задачі – означає знайти множину невід'ємних розв'язків си­стеми лінійних рівнянь.

Означення. Задачу лінійного програмування вважають записаною у канонічній формі, якщо вона задовольняє такі умови:

1. Система обмежень зведена до системи рівнянь виду (2.3).

2. Система рівнянь зображена в такому вигляді, де кожна ба­зова невідома входить тільки в одне рівняння системи з коефіцієн­том рівним одиниці, при чому немає рівнянь, в які не входила хоча б одна базова невідома. Якщо деякі рівняння системи поміняти місцями так, щоб нумерація базових невідомих була строго зрос­таючою, то базовий мінор в цьому випадку складає одиничну мат­рицю.

3. Вільні члени системи обмежень невід'ємні;

4. Оптимізуюча форма залежить тільки від вільних невідомих.

Отже, для того, щоб задачу лінійного програмування можна було розв'язувати симплексним методом потрібно загальну форму (2.1–2.2) звести до канонічної форми. Іншими словами її потріб­но певним способом записати в такій формі, щоб система рівнянь була з базисом.

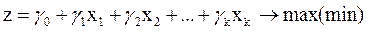(2.4)

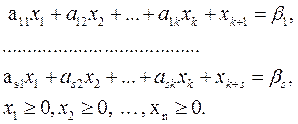(2.5)

Для того, щоби базовий план системи обмежень (2.4)був опорним, необхідно і достатньо, щоб всі вільні члени (2.5) були невід'ємні. Отже, для зведення задачі до канонічної форми потріб­но так підібрати базові невідомі, щоб у загальному розв'язку сис­теми обмежень не було від'ємних вільних членів.

Дата добавления: 2014-11-29