Гармония золотых пропорций 13 страница

Корбюзье успешно использовал функции Жолтовского в своем марсельском доме. Перед началом строительства дома был зало­жен символический камень шириной 86 см и длиной 183 см. «Этот крупный камень, − писал Корбюзье, − действительно, об­ладает изяществом, и он послужил для прославления модуло­ра...».

В соотношении размеров камня 86: 183 = 0,472... мы узнаем первую функцию Жолтовского, благодаря чему и возникло изя­щество, о котором упомянул Корбюзье.

Размеры камня (86 и 183 см) брались по величинам модуло­ра. Но в модулоре строились не все функции Жолтовского; полу­чалась главным образом лишь первая (0,472); вторая − воспроизводилась сложным путем, и практически не возникала и основ­ная функция. To же самое относится и к ряду других ценных в архитектурном отношении пропорций.

Таким образом, обладая в качестве системы пропорциониро­вания многими полезными качествами, модулор все же не создал возможностей для построения полной гаммы лучших архитектур­ных пропорций.

Упомянем еще об одном весьма существенном недостатке мо­дулора, пожалуй, принципиальном его недостатке. В своей основе система величин имеет одну модель человека. Только одного человека. Сразу же при разработке величин возникал вопрос, како­го человека взять за образец, и, по-видимому, как само собой ра­зумеющееся брался средний или выше среднего человек. В пер­вом варианте модулора он был ростом 175см, а в положении с поднятой рукой имел размер 216 см. От этих исходных величин и были подсчитаны все остальные.

Обычно средний человек мыслится более характерным и эта­лонным. Ho последующие исследования в специальных областях, связанных с проектированием оборудования и помещений со стро­го регламентированными условиями пребывания в них людей, по­казали, что подобные положения являются неправильными.

«Создание машины в расчете на „среднего человека" является серьезной ошибкой. Если машина спроектирована на основании данных величин, соответствующих 50-му перцинтилю любой груп­пы людей (т. е. средним значениям − А.П.), то ею смогут нор­мально управлять только 50%людей из этой группы. Например, 50% операторов более низкого роста будут не в состоянии дотя­нуться до органов управления. Следующая ошибка концепции „среднего человека" в том, что она игнорирует вариативность людей. Только у небольшого количества людей размеры могут быть средними во всех отношениях...». Далее в упомянутом труде следует вывод о необходимости проектирования не на сред­него человека, а на определенный размерностный диапазон людей и дается методика такого проектирования. Действительно, женщины, например, всегда меньше ростом и, если все делать по высокому или среднему человеку, для них многое в интерьере жилого помещения, на кухне и т.д. окажется недосягаемым и неудобным.

По-видимому, Корбюзье именно в этом ощущал недостатки своей системы, когда неоднократно менял модели людей. 3а первым следовал второй вариант модулора, с моделью человека ростом 183 см и размером в положении с поднятой рукой − 226 см Были и еще варианты. Все они существовали независимо один от другого, но целостной системы, в которой присутствовал бы необходимый диапазон моделей людей, у него не получилось.

Древнерусский «всемер»

Рассмотрим более развитый вариант системы величин пропор­ционирования, дополнив двухрядную модулорную схему новыми рядами Фибоначчи:

24 40

12 20 32 52

6 10 16 26 42

3 5 8 13 21 34 55

1,5 2,5 4 6,5 10,5 17 27,5 44,5

0,75 1,25 2 3,25 5,25 8,5 13,75 22,25 36 58,25 и т.д.Все горизонтальные линии являются здесь, рядами Фибоначчи (в средней части − третий и четвертый снизу − знакомые нам ряды схемы модулора). Во вновь дополненных рядах, так же как и в прежних, сумма двух предыдущих членов равна последующе­му, а отношение двух соседних приближается к величине золотого сечения (тем больше, чем дальше от начала ряда). По верти­кальным направлениям мы продолжили структуру удвоения ве­личин (вверх) и половинных значений (вниз); поэтому отноше­ние по вертикали составляют 1: 2: 4: 8....

В этой схеме каждый из горизонтальных рядов обладает ком­бинаторикой одиночного ряда Фибоначчи; каждая пара рядов комбинаторикой модулора Корбюзье, а весь комплекс величин − еще более высокими комбинаторными свойствами. Взаимозави­симости между величинами распространяются теперь на все их поле. Любую из величин можно получить множеством различных вариантов и комбинаций. Приводить все варианты мы, разумеется, не в состоянии, столь их мнoгo; покажем лишь на одном из при­меров возможное получение одной и той же величины слагаемы­ми разных рядов:

3 + 52 = 55

10 + 13 + 32 = 55

4 + 5 + 13 + 16 + 17 =55

2 х 3 + 2 х 6,5 + 2 х 8 + 2 х 10 = 55

Таким образом, рассмотренная нами схема обладает несравни­мо более высокими комбинаторными свойствами, чем две преды­дущие. Это обстоятельство является чрезвычайно важным для пропорционирования в архитектуре − одним из наиглавнейших. Однообразие, многообразие и возможность выбора зодчим желае­мого варианта компоновки зависят, в конечном счете, от количест­ва вариантов и их эстетического богатства или скудности. Имен­но по этой причине модулор Корбюзье оказался значительным шагом вперед − по сравнению с одиночным рядом Фибоначчи − и получил всеобщее признание. Рассмотренная же схема являет собой такой же, если не еще больший, шаг вперед по сравнению с модулором. Эта схема отображает систему величин, функцио­нировавших у нас на Руси еще за пять-шесть веков до Корбюзье, а может быть и ранее. Подобно модулору, она была связана также с системой мер и обладала многими замечательными свойствами. Как системе пропорционирования, мы дали ей условное наименование древнерусский «всемер», которое, по нашему мнению, должно отражать ее всеобъемлющий характер − функ­ционирование в архитектуре и в обычных мерных операциях.

Покажем присутствие в ней всех древнерусских (рассчитан­ных нами) саженей, о которых мы ранее говорили.

Выпишем в один ряд величины, завершающие вертикальные столбцы схемы, в порядке слева направо:

48 40 32 52 42 34 55 44,5 36 58,25

Напомним далее рассмотренные нами древнерусские сажени и разместим их в следующем порядке:

217,6 ∕ 49; 176 ∕ 39,5; 142,4 ∕ 32; 230,4 ∕ 52; 186,4 ∕ 42; 150,8 ∕ 34;

244 ∕ 55; 197,4 ∕ 44,5; 159,7 ∕ 36; 258,4 ∕ 58,25

В верхнем ряду (в числители) даны размеры саженей в сантиметрах; в нижнем же (знаменателях) − размеры в вершках с округлением до 1/4 вершка (1 вершок = 4,445 cм).

Выраженные в вершках размеры древнерусских саженей и их соподчиненные единицы совпадают с величинами только что рассмотренной схемы − обстоятельство, на котором мы специаль­но остановимся ниже.

Отклонения происходят лишь в начале ряда, в двух первых членах. Несовпадения представляют co6oй типичные отклонения, свойственные отношениям начальных членов ряда Фибоначчи от золотого сечения. Далее все последующие величины совпадают. Более полно система древнерусских мер представлена на рис. 7.В ее основе лежит схема, о которой мы говорили. Не­сколько видоизменено расположение величин, и они даются в сан­тиметрах. Все отношения величин уточнены по золотому сечению, и поэтому отношения начальных членов столь же «золотые», как и последующих. Вверху даются размеры древнерусских саженей. Они являются основными и исходными. Под каждой из них распо­ложены их половинные, четвертные, восьмые и т.д. доли, сла­гающие систему 1−2−4−8.... Каждая вертикаль представляет собой систему величин одной сажени особенность, на которую обратил внимание Б.А. Рыбаков: «Одним из существенных от­личий русской народной метрологии от древнегреческой, римской или византийской и западноевропейской метрологии является принцип постепенного деления на 2, когда меньшие меры полу­чаются путем деления большей на 2, на 4 и на 8... „Полуса­жень", „локоть", представляющий четвертую часть сажени, „чет­верть" или „четь", под которыми мы должны понимать четвертую часть полусажени („пядь"), − вот доли основной меры − саже­ни».

По диагональным направлениям снизу слева направо вверх величины образуют иные ряды. Эти ряды слагаются из мерных величин, относящихся к разным видам древнерусских саженей. Отношения строятся на золотом сечении, подобно величинам красной и голубой линий модулора Корбюзье. Диагональные ряды соотносятся между собой, как и линии, путем удвоения. Таким образом, каждая пара диагональных рядов представляет со­бой как бы модулор Корбюзье. Например:

20,78−32,62−54,4−88,02−142,4−230,4

16,81−27,2−44,01−71,21−115,2−186,4.

Здесь образуются удваивающиеся величины (расположены одна под другой), а смежные дают золотые отношения:

54,4: 27,2 = 2; 44,01: 27,2 = 1,618...

Мы могли бы даже назвать «цвет» линий: верхняя − голубая; нижняя − красная. Присутствует лишь новая модель человека. Ее рост 186,4 см; размер в положении с поднятой рукой − 230,4 см. Это высокий рост.

Таблица величин древнерусского «всемера» содержит много диагональных пар, и, следовательно, могут быть названы и дру­гие модели. Покажем их в общей структуре величин «всемера». В знаменателе дается рост; в числителе − размер в положении с поднятой рукой. Цифровые значения мы сопровождаем кратной словесной характеристикой роста с целью, передать наши общепо­нимаемые представления о различиях роста людей. Эти данные нам необходимы для последующего рассмотрения вопросов об­разности и масштабности в архитектуре, причем нашим требова­ниям будут удовлетворять даже весьма приближенные значения.

Согласуются ли сажени как единицы измерения с характером интерпретированных ими размеров − с ростом человека и с раз­мером человека до верха поднятой руки? Согласуются ли при этом они с антропометрическими данными?

Очень маленький рост	Маленький рост	Ниже среднего	Средний рост	Выше среднего рост	Высокий рост	Очень высокий рост
176,0 142,4	186,4 150,8	197,4 159,7	209,1 166,3	217,6 176,0	230,4 186,4	244,0 197,4

Общеизвестно, что «маховые» сажени представляют собой размах рук, а он, в свою очередь, передает рост человека. Дру­гой вид сажени - «косые», по своему определению являют собой размер человека от земли до конца пальцев максимально подня­той вверх руки.

Согласно антропометрическим измерениям, значения среднего роста, выше среднего и ниже среднего примерно совпадают. Сред­няя величина роста мужчины − 167,6 см. Граничные значения для 90% обследованных − 157,9 и 177,3 см. Значение величин «всемера» соответственно 166,3, 159,7 и 176 см. Остальные мы условно можем принять по характеру нарастания величин. Такое допущение не противоречит нашим требованиям получения лишь образных различий. Но нас интересуют больше люди в одежде, а не обнаженные, как их исследует антропометрия. Taк, напри­мер (рост дается, включая обувь), среднее значение − 175,3 см; граничные значения для 95% обследованных − 163,9 и 187,5 см. Данные величин «всемера» − 176, 166,3 и 186,4 см. Для город­ских женщин среднее значение роста − 159,5 см. Граничные зна­чения для 99% обследованных − 175,8 и 143,5 см. 3начения «всемера» − 159,7, 176 и 142,4 см. Наибольший рост как граничнoe значение для 99% обследованных составляет в одежде 190,3 + 6,75 = 197,05 см. В величинах «всемера» значение очень большого роста передается величиной 197,4 см.

Что касается наименований и кратких характеристик роста, то специальными исследованиями наших образных понятий о ро­сте человека на предмет их соответствия количественному значению антропометрических показателей мы не располагаем. Указанные нами характеристики и наименования роста могут считаться условными.

Обратим также внимание, что вопрос образного восприятия роста человека имеет свою историю. Некоторые выражения, свя­занные с понятием роста человека, в литературе даже XIX в. уже не воспринимаются нами так, как они воспринимались и понима­лись современниками. Без дополнительных пояснений смысл уже до нас не доходит. Например: «В нем, как в Петре Великом, 15вершков роста» (Лесков. Несмертный Голован). В буквальном смысле можно понять, что рост Петра был 15 х 4,445 = 66,7 − карликовым. В обиходе для упрощения не называлась еще малая сажень 142 см (равная 32 вершкам), от которой велся отсчет. Подобно тому как, например, в нашем выражении «весной сорок третьего» означает весной 1943 г., а не весной 43 г. н. э. Поэтому рост был 142,3 + 66,7 = 209 см − баскетболистский, сверхвысокий.

Отметим здесь два момента. Характерно, что вершковая мера, как видно по ее названию, полагает наличие базовой величины, сверх которой (выше которой) она отсчитывается. Базовой величиноймог быть лишь минимальный рост, но не средний, так как небольшие роста выражались бы тогда в отрицательных числах. Минимальным ростом ибыла сажень, носившая название «малая» и она справедливо попадает в наш ряд на место минималь­ного эталона роста. Второй момент − применение в обиходе вершковой меры для передачи характерных различий в размерах роста. Этот вопрос нас весьма интересует. Именно зрительное восприя­тие размеров роста человека, не инструментальное, а зрительное и образное. Архитектура строится на образных восприятиях. Одна форма больше, другая − меньше. Насколько надо сделать меньше, чтобы выглядело меньше? Допустим, мы имеем квадрат со стороной 100. Будет ли он восприниматься прямоугольником, если одну из сторон сделать 99? Или он будет казаться небрежно выполненным квадратом? Сколько следует отнять, чтобы он стал выглядеть прямоугольником с минимальным различием сторон?

Архитектура − антропоморфична, поэтому количественное со­держание образных восприятий человека всегда интересовало зодчих и в системах пропорционирования должны были содержаться только нужные значения, а промежуточные и ненужные выбрасывались.

Размеры саженей, передающие рост человека (в вершках):

32−34−36−38−40−42−44,5.

3десь мы видим разгадку, объясняющую, почему абстрактные числа рядов Фибоначчи в схеме древнерусского «всемера» превра­тились в модели людей после придания им вершковой размерно­сти. Это не было случайным совпадением. Вершок, как видим, является модулем зрительного различия человеческого роста, и поэтому с его помощью в литературе XIX в. слагались понятия о росте человека.

Все виды саженей и величин, упоминавшихся ранее, нашли свое место в системе моделей людей, кроме величин 258,4 и 134,5 см, присутствие которых в древнерусской архитектуре было показано на ряде примеров. Первая из величин превышает са­мую большую сажень, а вторая меньше самой малой. С помощью некоторых других саженей составим еще две модели − «больше самой большой» и «меньше самой малой»:258,4 ∕ 209,1 и 166,3 ∕ 134,5; необходимость наличия таких моделей в системе пропорциониро­вания заключается, по-видимому, в следующем: любая вещь или предмет, контактирующий с человеком, обычно не равняется че­ловеку, а выполняется либо больше, либо меньше человека. Дверной проем, спальное место − больше человека, а верхняя полка должна быть меньше человека с поднятой рукой, чтобы он мог дотянуться. Размер предмета, элемента сооружения вы­полняется практически на ступень больше или на ступень меньше модели соответствующего человека. Для максимальной и мини­мальной модели нужна, следовательно, еще ступень для выпол­нения размеров «человек плюс зазор» и «человек минус зазор», что мы и находим в величинах «всемера».

Древнерусское искусство

пропорционирования

Мы остановимся на следующих вопросах:

соразмерение сооружений с человеком;

масштабность элементов сооружения по отношению к чело­веку;

реставрационные работы на основе исследования приемов древнерусского искусства пропорционирования.

Подытоживая ранее сказанное, мы приходим к следующим выводам: древнерусский зодчий при назначении основных фор­мообразующих размеров сооружения, в выборе тех или иных видов саженей и при нахождении их количеств руководствовался определенной логикой. Именно этим вопросам он уделял весьма серьезное внимание, чем существенно отличался от современного зодчего.

В скульптуре, в размерах помещений, в толщинах кремлев­ских стен присутствовали, как мы показали во II разделе, caжениодного и того же вида и в количествах 2 − 2¹/_z − 6 − 12... единиц, т.е. предпочтительные количества. Выше было показано, что все сажени представляли coбoй основные параметры моделей людей. 3одчий, следовательно, мог мыслить саженью того или иного вида как образом соответствующего человека. В то же вре­мя величины, которыми он оперировал, обладали наивысшими комбинационными свойствами. Это также отвечало специфике архитектурного мышления древнерусского зодчего.

Воспользуемся прежними примерами и продолжим наше рас­смотрение.

Познакомимся с размерами, которые избрал зодчий для палат митрополита в Крутицах. Общая суммарная длина основных по­мещений − 12 сажен церковных (22,32 м). Этот размер был исходным. Для палат самого митрополита зодчий избрал греческие сажени − в них выполнил спальню и столовую. Размер каждой из палат по фасаду 2 х 230,4 = 461 см, или по 2 греческих сажени. Помещение заместителей − 4 х 142,4 = 576 см. Сажени взяты уже малые и в количестве 4. Но поскольку на двоих, то на каж­дого получается также по 2 сажени. Вестибюль − 4 сажени − по l34 см (название саженей мы не знаем). Палата приемов − 3½ сажени церковных по 186,4 см (см. рис. 8).

Рассмотрим несколько весьма характерных принципов про­порционирования, которые отчетливо выражены в данном решении.

1. Вид саженей в главных формообразующих размерах соору­жения соответствует назначению сооружения − 12 церковных са­женей. Церковные сажени − для церковной постройки.

2. Для разных по своему значению и положению в иерархической лестнице людей создаются помещения, размеренные со­ответственно разными видами саженей. Митрополиту гречески­ми, по 230 см; заместителям − малыми, по 142,4 см.

3. Удвоенным числом саженей устанавливается соразмерение между человеком и помещением. Такое соразмерение мы назы­ваем масштабностью элементов сооружения по отношению к че­ловеку. Следовательно, масштабность помещений равна 2. Подобное понимание масштабности для нас необычно. Но, так как древнерусский зодчий пользовался комплексом моделей людей, величина соразмерения форм архитектуры с человеком выража­ется в древнерусской архитектуре только с учетом параметров соответствующей модели и, следовательно, соответствующего вида саженей.

Перечисленным принципам отвечали все исследованные нами памятники архитектуры.

Возьмем, например, постройку патриарха Никона на Кий-острове – Крестовоздвиженский собор. Его длина − 22,37 м, что представляет собой 12 церковных саженей по 186,4 см; напом­ним длину церкви Параскевы Пятницы в Новгороде − 12 са­женей по 176 см, называвшихся «народными» или «лавочны­ми» − ее построили представители торгового сословия на Ве­чевой площади в послекняжеский период, в 1207 г. Георгиевский собор Юрьева монастыря в Новгороде наиболее ярко выраженное сооружение княжеского периода, имеет длину 10 великих саже­ней по 244 см и ширину 8 царских саженей по 197,4 см.

Виды саженей, как видим, строго соответствуют социальному положению заказчика. Пока мы не обнаружили ни одного исключения из этого правила, исследовав несколько десятков соору­жений.

Принцип двухкратной сомасштабности помещений человеку также шел, по-видимому, от глубокой древности. Достаточно вспомнить печурку (пещерку), которую в XI в. отшельник; Илларион «ископа себе». Ее размер и вид саженей четко указаны: «малу дву сажен». В XIX в. архитектор Жилярди, автор усадьбы и парка в Кузьминках, рассчитал жилую площадь дома обслу­живающего персонала па 14 семей, исходя из 2 саженей по фа­саду на семью, что дало площадь в среднем 12 кв. саженей на семью (сажени в XIX в. были уже только одного вица: 1 са­жень = 213,36 см).

Любопытно, что наша современная норма жилой площади на человека − 9 кв. м − представляет собой также 2 также 2 кв. сажени (по 2,13 м).

Но вернемся к палатам митрополита. В помещениях, нося­щих общественный характер, где присутствует несколько чело­век (палата приемов, вестибюль), число саженей увеличивается, однако не прямо пропорционально возможному числу людей. 3десъ зодчий придерживается некоторых ровных чисел 4−6­− 12, иногда символичных (7 полусаженей в палате приемов). Воз­можно, что исходные размеры (типа 12 саженей церковных) были зафиксированы на измерительном шнуре или такой была длина самого шнура.

Далее зодчий членил исходный размер по каким-то известным ему соотношениям и получал то, что требовалось. Исследование вариантов членения исходных размеров показало чрезвычайное разнообразие различных членений.

В митрополичьем дворце зодчий сначала поделил исходный размер пополам: 12 саженей по 186 см (6 саженей по 186 см) + (6 саженей по 186 см). 3атем одну из половин оп членит так:

6 саженей по 186 см = (4 сажени по 142 см) + (4 сажени по 134 см).

Полученными размерами образует помещение заместите­лей и вестибюль. 3десь следует сразу же обратить внимание на получившиеся пропорции по функции Жолтовского:

(4с 134): (4с 142) = 0,944 = 2 х 0,472 = 2 хFж₁,

Отношение составило удвоенную первую функцию Жолтов­ского. Ее художественный смысл мы рассмотрим в одном из последующих примеров. Пока лишь заметим, что отношение дает минимальное различие размеров, воспринимаемых зрителем. Вторая половина (столовая и палата приемов) отличалась более контрастным отношением:

6 саженей по 186 см = (2 сажени по 230 см) + (3½ сажени то 187 см).

Отношение этих размеров может быть выражено также через систему функций Жолтовского, но по характеру сложности в данной работе мы их не рассматриваем.

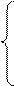Сравним расчленение тех же 12 сажeнeй 186 см в Крестовоз­двежeнcкoм соборе на Кий-острове. В продольном направлении размеры западного, центрального и восточного нефов, размеры столбов и апсид слагают оригинальную последовательно убываю­щую структуру:

4 сажени великих (нартекс и алтарь)

3 сажени церковных (подкупольный квадрат) 12 саженей

2 сажени царских (столбы) церковных

1 сажени греческих

½ сажени простой

Пропорции каждой из палат в Крутицком дворце (отношение длинны к ширине) также заслуживают внимания. Спальня, например, квадратная. Как известно, квадрат является статичной фоpмoй и не имеет развития ни по одной из осей (длина и шири­нa одинаковы). Квадрат композиционно ненуждается в поддерж­ке другими формами. Поэтому спальня вынесена. В спальне че­ловек пребывает значительное время и eмy не требуется связь с другими палатами. Центральное место среди всех помещений за­нимает палата приемов, с oднoй стороны от нее покои митропо­лита, с другой − помещение для посетителей и заместителей. Да­леe в обе стороны по переходам можно попасть в Воскресенскую, Петропавловскую и Успенскую церкви. Центральному местопо­ложениюпалаты отвечают и ее специфические пропорции.

Длина к ширине составляет отношение − 1,118..., равное основине составляет отношеттие -оиап церковныхной функции Жолтовского. Сам И.В. Жолтовский назвал прямоугольник такой формы «живым квадратом». В отличие от геометрического квадрата его форма наиболее статична и не изолируется от других форм. Живой квадрат является первым после квадрата прямоугольником, зрительно воспринимаемым как пря­моугольник с наименьшим различием сторон. Живой квадрат очень часто образует центральное ядро композиции, так как об­ладает необходимым для этого сочетанием качеств: статичностью и выразительностью «начала движения», «начала роста».

Интepecнo также соотношение размеров помещений митропо­лита с помещениями заместителей. Если предположить, что перегородка делила площадь пополам, то: (2 саженей по 230 см): (2 саженей по 142 см) = 1,618..., т. е. в золотом сечении. Так выражалась соподчиненность размеров помещений.

Следует обратить внимание, что во всех мерных операциях брались размеры помещений в чистоте − без учета толщин стен, т.е. размеры только функционально используемых площадей. Толщина конструкций как бы игнорировалась, хотя внутренние поперечные стены, в отличие от современных перегородок, вы­полнены не менее 62см. Иначе размерялись формы, рассчитан­ные только (или главным образом) на зрительное восприятие: главы, шатры, декоративные элементы фасадов и т. д. Основные размеры в зтом случае относятся к внешним контурам габаритам.

Вернемся к Строгановским постройкам. Мы рассматривали ордерные композиции, которым, как известно, свойственны черты антропоморфизма (передача в обобщенной форме образа человека). Всюду зодчие применяли 2½ кратность по отношению к соответствующей модели человека. Это масштаб. Какие же полу­чились соотношения? В трех случаях (см. рис. 6) одни и те же 2Fж₁ −удвоенная первая функция Жолтовского: 2 х 0,472 = 0,9444... Что дает и что выражает отношение 2Fж₁?

Это минимальная характерная доза различия для сопостави­мых элементов. Величина, которая в наших понятиях роста человека создает различие одной категории роста от другой. Высокий и очень высокий, средний и выше среднего человек и т.д. Та­ким образом, зодчий представил нам на фасадах антропоморфич­ные декоративные элементы − колонны − одни выше, другие ниже − с минимальной разницей в размерах и в полном соответ­ствии с нашими образными представлениями о различиях роста людей.

В Казанской церкви в Устюжне отношение принимается бо­лее сложное и с большим контрастом: Ф ∕ 2Fж = 0,91. Причем в Казанской церкви, в отличив от других церквей, ордер верхнего яруса больше, чем нижнего. Причина такого решения, по-види­мому, в кладбищенском назначении Казанской церкви. Верхний ярус, как более тяжелый, оказывает давление на нижний, и впе­чатления легкости, радостности невозникает.

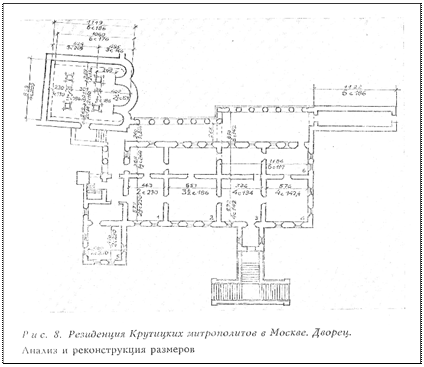
Среди крутицких построек (рис. 8, 9 ) весьма примечательным является теремок, хотя по назначению это всего лишь ворота с переходом, но по оригинальности решения и совершенству пропорций − уникальное высокохудожественное произведение. В нем сочетаются живопись, керамика, резной камень. О ширине теремка мы говорили − 6 саженей церковных по 186,4 см (размер наружный). В теремке в его основных габаритах так же встре­чается 2½ кратность. Высота уровня пола перехода составляет 2½ сажени греческих; высота до карниза 2½ сажени 2 х 244 см − удвоенных великих. Но в ордерном декоре кратность иная. Раз­меры колонн первого яруса - 2 сажени народные по 176 см; колонн второго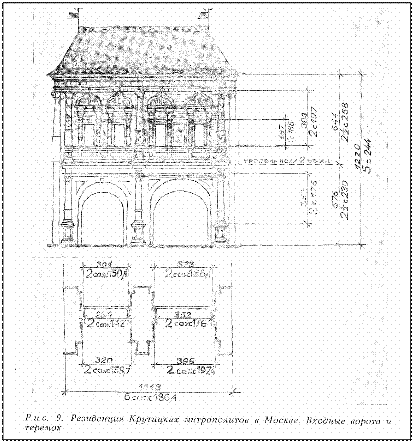

яруса − 2 сажени царские по 197,4 см; колонки в наличниках окон − 1

сажень по 186,4 см. Масштаб колонн первого и второго ярусов равен 2; масштаб колонок в налични­ках равен 1. Отношения дают полную гамму функции Жолтовского: (2 сажени по 197 см): (2 сажени по 176 см) = 528: 472 = 1,12 = Fж, а малые колонки в наличниках окон к ярусным колоннам:

(1 сажень по 187 см): (2 сажени по 197 см) =0,472: 1 = 0,472 =Fж₁,

(1 сажень по 187 см): (2 сажени по 186 см) = 0,528: 1 = 0, 528 = Fж₂.

Еще раз обратим внимание на эти уникальные соотношения, а также и на присутствие двух масштабов в однотипнъrх элементах декора.

Основные габаритные размеры, о которых мы говорили (2½ сажени по­ 230 см и 2½ сажени 2 х 244 см), составляют, отношение по первой функции Жолтовского, равное 0,472 = Fж₁. на фасаде теремка его ширина к высоте относится по уже известной нам сложной функции Ф ∕ 2 Fж₁.

(6 саженей по 186 см); (2½ сажени 2 х 244 см) = 0,91 = Ф ∕ Fж.

Знание приемов древнерусского искусства пропорционирования позволяет в ряде случаев находить размеры формы и габариты элементов для утраченных частей памятников архитекту­pы, что бывает весьма необходимо при реставрационных работах.

Taк, например, в практике работы реставрационной мастерской ЭСНРПМ ЦС ВООПиК путем применения методики, основанной на рассматривавшихся нами принципах, были определены или уточнены габариты, формы и размеры многих утраченных элементов и деталей, следы которых не сохранились или сохранились в недостаточных количествах. Вычислялись размеры окон­ных наличников, крылец, дверных проемов, полотнищ дверей, ворот, сечения столбов и т.п.

Дата добавления: 2014-12-07