Гармония золотых пропорций 14 страница

Познакомимся с некоторыми приемами таких вычислений. Воскресенская церковь Крутицкого дворца перестраивалась в XVII в. Барабан и столбы были ликвидированы. С тех пор про­шло более 300 лет. На первом этаже сохранились основания, по которым могли быть примерно определены лишь, оси столбов.

Размеры столбов по оставшимся следам установить не удалось. Задача заключалась в нахождении сечений столбов и пролетов между ними. Методика поиска в данном случае строилась на увязке различных вариантов сечений со всеми остальными вели­чинами, слагающими главные формообразующие размеры − дли­ну и ширину помещения. Задаваясь различными вариантами се­чений, мы получали соответственно различные варианты разме­ров нефов, алтаря и подкупольного квадрата. Получение всех величин в целых завершенных числах соответствующего вида са­женей означало нахождение искoмoгo решения. Один из вариан­тов дал приемлемые результаты. Размеры столбов 93 х 93см (что равно 1/2 сажени по 186 см х 1/2 сажени по 186 см) и члене­ние по длине: 6 саженей по 186 см =1 сажень по 230 см + 1 са­жень по 186 см + 2 сажени по 150 см + 2½ сажени по 159 см.

Далее методика требует подтверждения полученного резуль­тата еще какими-то другими данными, например сопоставлением со столбами в аналогичных зданиях. Размер ½ сажени по 186,4 см − один из распространенных для столбов небольших сооружений и бы л подтвержден рядом примеров. Более серьезной работой явилось вычисление размеров шатра Воскресенского со­бора Ново-Иерусалимского монастыря, уничтоженного в послед­нюю войну (рис. 10). Размеры шатра вплоть до настоящего вре­мени не были известны, и начатые работы по его восстановлению были поэтому приостановлены.

Несмотря на то что шатер является сугубо русским элемен­том архитектуры и во многих теоретических работах шатры под­вергались самым разнообразным и всесторонним анализам, не существовало практически пригодной методики для установления хотя бы приближенного значения высоты шатра применительно к Hово-Иерусалимскому храму. Вопрос не находил решения дол­гое время. Нам потребовалось буквально несколько минут для получения основных размеров в первом приближении. Сложнее и несколько больше времени заняло вычисление подтверждающих размеров, деталировочных размеров и других параметров и форм шатра.

Напомним краткую историю памятника. В начале XVII в. патриарх Никон приступил к строительству под Москвой в о6лю­бованном им месте, в районе Истры, Ново-Иерусалимского монастыря. Главное здание − Воскресенский собор − предполагалось воздвигнуть по типу соответствующего храма в Иерусалиме с повторением его отдельных форм и размеров, но с поправкой на древнерусские традиции и условия. В храме также устанавлива­ется «гроб господен» и также во дворе круглой формы, но двор обносится высокой стеной и перекрывается шатром. Первый ша­тер существовал недолго. Пocлe его обрушения на тех же сте­нах в XVIII в. возводится архитекторами Растрелли и Бланком шатер с большим числом остекленных проемов (60 люкарн). Шатер Растрелли-Бланка простоял 200 лет и был уничтожен во время последней войны. Cтех поp − около 40 лет − здание находится без шатра.

Обмеры первоначального шатра производились в XVII в., и мы упомянули их результаты. Шатер по высоте равнялся тогда 12 саженям церковным по 186,4 см (22,37 м)Обмеры шатра!Растрелли-Бланка не выполнялись. О его облике можно судить по сохранившейся фотографии с общим видом монастыря. Фото­графия снята в конце XIX в. К тому же периоду относятся за­меры некоторых деталей шатра. И, наконец, сохранился еще чертеж с проектом Растрелли, по которому возводился в ХVIII в. второй по счету шатер. Пользуясь сохранившейся фотографией, фотограмметристы пытались определить высоту шатра. Но, ­по-видимому, применение различных методов привело к результатам несколько различным один от другого.

Шатер на проекте Растрелли также сильно отличается от построенного им же самим шатра, и поэтому проектом Растрелли практически нельзя руководствоваться при восстановительных работах. Что касается замеров деталей шатра, то они имеют вид черновика и размерные детали в них не вполне ясны.

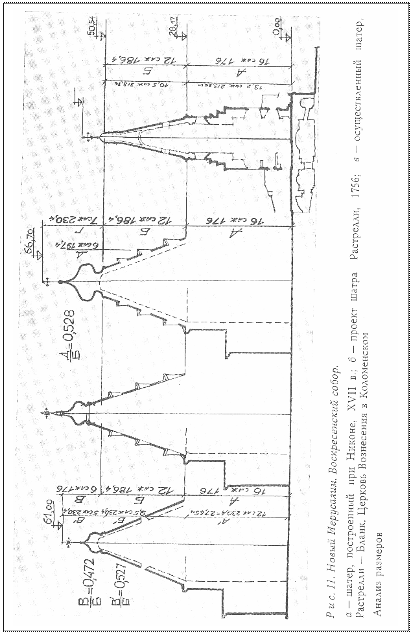
Архитекторы, реставрирующие Ново-Иерусалимский монастырь, по-разному истолковывая все эти материалы, не пришли к единому мнению о размерах шатра и дали сильно отличающиеся один от другого проекты. (рис. 11).

Мы начали со стены, на которой покоился шатер. Упоминалось, что ее высота 28,17 м. Такой же по высоте и восьмерик церкви Вознесения в с. Коломенском. А сумма трех ярусов Рождественской церкви в Горьком дает половинную величину – 14,08 м. Ясно, что перед нами один из характерных древнерусских размеров. Вполне вероятно, что шатер также мог выполняться в каком-либо характерном размере. И мы можем сделать предварительное предположение о его величине.

Высота шатра церкви в с. Коломенском 22,37 м. Высота первоначального шатра никоновского периода – 22,37 м. Подобного рода сопоставления наводят нас на мысль о возможном таком же размере второго шатра. Но это требует дополнительных подтверждений, хотя величина в 12 церковных саженей представляется и весьма убедительной для шатра такого собора, как Воскресенский, не только в XVII в., но и в XVIII в. Предположенный нами размер шатра нашел много косвенных подтверждений. Рассмотрим одно из них, связанное с характером архитектурных пропорций.

В первоначальномшатре размер главы с крестом был 10,56 м, что по отношению к высоте шатра составляло:

10,56: 22,37 = 0,473...

В отношении легко узнается первая функция Жолтовского. Первоначальное сооружение имело, как видим, изысканные пропорции.

В проекте Растрелли шатер показан (если взять по линейно­мy масштабу) размером 26,2 м,а глава с крестом − 12,3 м. Отношение составляет:

12,3: 26,2 = 0,474...

Точно такое же как в никоновском шатре, хотя Растрелли изменил общую высоту сооружения, увеличив ее примерно на 5-6 м.

Почему Растрелли увеличил высоту? Видимо, по соображе­ниям чисто художественного порядка. В соборе центральное зда­ниe представляет собой кубический объем, увенчанный главой большого диаметра. Композиционно центральный объем нуждался в соседстве с более стройной и вытянутой формой. Повышая ша­тер, Растрелли вносил в общую композицию полезные коррективы. Однако, повторяем, это было лишь в проекте, а построенный шатер отличался от изображенного на проекте.

Сопоставление форм сооружения на проекте и на натурной фотографии подсказывает, что разница в высоте шатра составила 4 м, но высота всего сооружения примерно совпадала. Включая крест, она по линейному масштабу измерялась от уровня чистого пола в 66,7 м и могла трактоваться с учетом понижения планировочных отметок земли по сравнению с полом как 36 церковных саженей:

36 х 186,4 = 67,1 м.

Причина изменения пропорций состояла, по-видимому, в за­мене запроектированных кирпичных стен шатра на обшивку по наклонным деревянным фермам, занявшим большой строительный объем, что и привело к перепропорционированию шатра и главы. Верхнее основание шатра увеличивалось (зодчий не пожелал сужать шатер вовнутрь и портить интерьер). Глава, венчающая шатер при этом также требовала расширения; соответственно ее высота должна была увеличиться, так как в главах диаметр и высота взаимосвязаны. Шатер поэтому пришлось уменьшить по высоте. Растрелли в проекте изобразил шатер высотой в 26,2 м, или при переводе в церковные сажени − 14 саженей (по 186,4 см).

Вполне вероятно, что при необходимости уменьшения высоты шатра ее сократили до 12 саженей получили традиционный раз­мер − 22,37 см.

Результаты анализа на архитектурные пропорции согласуются с этим значением. Оказалось, что только при высоте шатра в 12 саженей церковных (22,37 м) и высоте главы в 6 саженей царских (11,84 см) получаются эстетически совершенные про­порции.

11,84: 22,37 = 0,529....

в чем мы узнаем вторую функцию Жолтовского. Отношение хотя и иное, но сохраняет с первым как бы родственные черты. Это отношение взято по контуру геометрической формы шатра. Но позолоченное покрытие создавало еще и другое четко читае­мое членение. Верхняя часть шатра имела покрытие из таких же позолоченных медных листов, что и сама глава, которое шло по­лосой ниже главы и ее шейки примерно па 1,2 м. В зтом случае членение берется по линии, разделяющей виды и цвет отделоч­ных материалов. Линия, разграничивающая золотое от белого, членит общую форму иначе. Она проходит на высоте:

22,37­ − 1,2 = 21,2 м.

Завершение увеличивается

11,84 + 1,2 = 13,05 м.

Тогда отношение составит

21,2: 13,05 = 1,62.

Это золотое сечение. Полученные размеры также пересчиты­ваются в древнерусские сажени. 21,2 = 12 саженям по 176 см; 13,05 = 7 саженям по 186 см.

Высота позолоченного завершения, равная 7 саженям церков­ным (13,05 м), отнесенная ко всей нижележащей части сооруже­ния, дает величину 1∕2 х 0,528 − равную половинной величине второй функции Жолтовского.

Варианты других размеров всех упоминавшихся элементов, выраженные в целых и дробных числах саженей, не дали столь стройной системы эстетически совершенных пропорций, что и служит одним из косвенных подтверждений правильности пред­полагаемой высоты шатра 22,37 см.

Проводились и другие виды проверочных расчетов − на по­строение иразбивку двадцатигранника (шатер представлял собой двадцатигранную усеченную пирамиду), на разбивку люкарн и др. Они дали согласующиеся результаты, и мы можем сказать в итоге, что высота шатра 22,37 см является весьма вероятной. Среди архитекторов, занимавшихся реставрацией Ново-Иеру­салимского монастыря, проектные решения ближе всего оказались к вычисленным В.Л. Малхасовым.

В заключение вернемся к храму Василия Блаженного и пока­жем в нем некоторые оригинальные приемы пропорционирования. В группе окружающих церквей размеры глав с крестами в их отношении к высоте центральной церкви Покрова дают такую же половинную величину второй функции Жолтовского (высота главы с крестом восточной церкви 16,7 м; высота церкви Покро­ва − 63,2 м):

16,7: 63,2 =1/2 x 0,528.

В храме Василия Блаженного зодчий связал традиционными пропорциями главы окружающих церквей с центральной доми­нантой ансамбля. Эти главы по местоположению принадлежат столпам, на которых они водружены, но одновременно и по тра­диционным пропорциям связаны с центральным элементом ан­самбля. Подобными приемами пропорционирования зодчий добил­ся общей слитности и единства ансамбля, состоящего из девяти разрозненных зданий, и проявил глубокое понимание специфиче­ских принципов этого искусства.

Храм Василия Блаженного являет собой также характерный для древнерусской архитектуры пример антропоморфизма не только в элементах декора, но и в облике целых сооружений с варьированием в широком диапазоне моделей и масштабов.

Окружающие церкви слагают два уровня высот. Если взять их размеры от земли до центров глав − как бы по зрительным центрам их тяжести, то выделяются уровни 22,8 и 29,8 м, кото­рые переводятся в 16 саженей малых (по 142,4 см) и 16 саже­ней по 186,4 см. Образно отображаемые модели людей составляют диапазон от caмoгo маленького роста до большого, но не вклю­чают наибольший, отданный центральной церкви Покрова. Ее вы­сота (63,2 м) слагается из 32 саженей по 197,4 см − «царских» − самых больших ростовых да еще в удвоенном количестве, т.е. в двойном масштабе.

В своем образе храм являет нам диапазон человеческих раз­личий свойственный большому сообществу людей − народу, − в композиции с центральной пирамидальной формой, значимость которой подчеркивается увеличенным масштабом.

Приложение 3

Полный комплекс саженей

Таблица 1

Сажени		1,5		2,5
Пилецкого	2,055	3,083	4,110	5,138
Египетская	1,663	2,495	3,326	4,157
Меньшая	1,345	2,018	2,690	3,363
Казенная	2,176	3,264	4,352	5,440
Народная	1,760	2,640	3,520	4,400
Малая	1,424	2,136	2,848	3,560
Греческая	2,304	3,456	4,608	5,760
Церковная	1,864	2,796	3,728	4,660
Простая	1,508	2,262	3,016	3,770
Великая	2,440	3,660	4,880	6,100
Царская	1,974	2,961	3,948	4,935
Кладочная	1,597	2,396	3,194	3,993
Большая	2,584	3,876	5,168	6,460
Фараона	2,091	3,137	4,182	5,228
Городовая	2,848	4,272	5,696	7,120

Локти комплекса саженей

Таблица 2

Сажени		1,5		2,5
Пилецкого	0,514	0,771	1,028	1,284
Египетская	0,416	0,624	0,8315	1,039
Меньшая	0,336	0,5045	0,6725	0,8407
Казенная	0,544	0,816	1,088	1,360
Народная	0,440	0,660	0,88	1,100
Малая	0,356	0,534	0,712	0,890
Греческая	0.576	0,864	1,152	1,440
Церковная	0,466	0,699	0,932	1,165
Простая	0,377	0,5655	0,7543	0,9425
Великая	0,610	0,915	1,220	1,525
Царская	0,494	0,740	0,987	1,234
Кладочная	0,399	0,599	0,7985	0,9983
Большая	0,646	0,969	1,292	1,615
Фараона	0,523	0,7842	1,045	1,307
Городовая	0,712	1,068	1,424	1,780

Литература.

1. Математический энциклопедический словарь. – М.; «Сов. Энцик.», 1988.

2. Черняев А.Ф. Русская механика. - М.,: Белые Альвы, 2001.

3. Клайн М. МАТЕМАТИКА. - М.: Мир, 1982.

4. Риман Б. О гипотезах, лежащих в основании геометрии. - М.,: Мир, 1979.

5. Словарь иностранных слов. – М.; Советская энциклопедия, 1964.

6. Митрохин А.Н. О взаимодействии размерностей в математических преобразованиях. - М.,: Транспорт, 1996.

7. Кузанский Николай Соч. в двух томах. Т. 2., «Мысль», 1980.

8. Стахов А.П. Сакральная геометрия и математика гармонии. Вiнниця; ТОВ. «IТI», 2003.

9. Что, зачем, почему? Большая книга вопросов и ответов. – М., «Экспо», 2003.

10. Пуанкаре А. Наука и гипотеза. - М.,: Наука, 1984.

11. Эйнштейн А. Геометрия и опыт. Собр.труд. Т. 2. - М.: Наука, 1966.

12. Линдер Г. Картины современной физики. - М.,: Мир, 1977.

13. Куликовский Г.Г. Справочник любителя астрономии. - М.,: Наука, 1971.

14. Черняев А.Ф. Структура космологического красного смещения

15. Струве О. и др. Элементарная астрономия. - М.,: Наука, 1964.

16. Библия - М.,: Российское библейское общество, 2001.

17. Колмогоров А.Н. и др. Геометрия. - М.,: Просвещение, 1979.

18. Погорелов А.В. Геометрия. – М.; Просвещение, 1992.

19. Выгодский М.Я. Справочник по элементарной математике. - С-Пб.,: 1994.

20. Клиффорд В. О пространственной теории материи. Сборник статей Альберт Эйнштейн и теория гравитации. - М.: Мир, 1979.

21. Ленин В.И. Материализм и эмпириокритицизм. – М.; Политиздат, 1949.

22. Владимиров Ю.С. и др. Пространство, время, гравитация. - М.,: Наука, 1984.

23. Черняев А.Ф. Золото Древней Руси. - М.,: Белые Альвы, 1998.

24. Шевелев И.Ш., Мурутаев М.А., Шмелев И.П. Золотое сечение. – М.: Стройиздат,1990

25. Пилецкий А.А. Система размеров и их отношений в древнерусской архитектуре. Сборник. Естественно научные знания в Древней Руси. - М.,: Наука, 1980.

26. Черняев А.Ф. Тарасова С.В. Диалектика пространства. - Сн-П., 1994.

27. Щербаков Р.Н., Пичурин Л.Ф. От проективной геометрии к неевклидовой. – М.: Просвещение, 1979.

28. Волков Ю.В. Черняев А.Ф. Гравитация и антигравитация. – М.; 2003.

29. Мулдашев Э.Р. В поисках города Богов. - М.,6 Аиф-Принт, 2001.

30. Коробко В.И., Коробко Г.Н. Золотая пропорция и человек. – М. Изд. АСВ., 2002.

31. Черняев А.Ф., Тарасова С.В. Золото Руси. - М., 1995.

32. Наука и религия − №7, 2002.

33. Девис П. Суперсила. - М.,: Мир, 1989.

34. Канарев М.Ф. Новый анализ фундаментальных проблем квантовой механики. - Краснодар, 1990.

35. Якушин А.Н. Количество и пространство. - Колпино, 1998.

36. Дирак П. Воспоминания о необычайной эпохе. – М.: Наука, 1990.

37. Петухов В.С. Биомеханика, бионика и симметрия. - М.,: Наука, 1981.

38. Пилецкий А.А. Золотое семейство. Приложение к строительной газете. - М., 6 17 января 1982.

39. Черняев А.Ф. Удалова С.Н. Время пирамид. Время России. – М.: Белые Альвы, 2000.

Содержание

Преамбула 3

Глава 1

Диалектика математики

1.1. Целое и отдельное в познании 7

1.2. Отдельное как целое. 11

1.3. Введение в диалектику математических понятий 17

1.4 Математические иллюзии 26

1.5. Диалектические законы в математике 40

1.6. Идеология пространственной бесконечности 51

1.7. Качественные аспекты математики 63

1.8. Свойства фигур евклидовой геометрии 75

1.9. Диалектика элементов геометрии 78

Глава 2

Дата добавления: 2014-12-07