Гармония золотых пропорций 12 страница

Внутренняя ширина с притворами - 12 саженей - 150,8 см.

Итак, три основных размера в одном здании выражаются тремя разными видами саженей. Ранее почти все исследователи древнерусской метрологии отмечали обилие различных видов саженей, но не предполагалось одновременное их применение в одном сооружении. Представлялось непонятным производить измерения несколькими видами саженей. Впервые Б. А. Рыбаков четко сформулировал казавшееся невероятным положение об одновременном применении в одном сооружении нескольких видов саженей. Ниже мы убедимся, что установленный им принцип является обязательным. Применяя лишь один вид са­женей, древнерусский зодчий построить сооружение не мог, он столкнулся бы со сложными дробями и без ЭBM не справился бы с вычислениями. Несколько саженей и соподчиненных им единиц сводили почти все размеры к целым завершенным, легко запоминаемым и символически осмысленным числовым выраже­ниям.

Итак, по 12 саженей, но разных.

Сажень 176 см. Главным размером, как показывает наш опыт, является длина сооружения. И, действительно, 12 саженей по 176 см составляют размер 21,1 м, который Ф. И. Петрушевский называет среди древних мер Вавилона, Персии и Мидии «снуром персов». Говорить о заимствовании данной меры от персов, по-видимому, не следует, в чем далее мы убедимся. Но совпаде­ние примечательно. Половина такого размера - 10,55 м, равных 6 саженям по 176 см, − также характерная и частоупотребимая величина. Мы встречаем ее, например, в первом этаже Воскре­сенской церкви в Крутицах, где помещалась казна. Это длина помещения казны. Система величин, базирующихся на сажени 176, довольно развита. Ряд ее наименований - «народная», «ла­вочная», «мерная» − передает и ее происхождение. Она вос­производилась размахом рук человека среднего и выше среднего роста, т. е. наиболее распространенной антропометрической кате­горией людей.

Укажем еще на серию характерных размеров, связанных с этой саженью: 28,17 м = 16 саженей; половинный размер − 14,08 м = 8 саженей и 7,04 м = 4 сажени.

Размер 28,17 м мы встречаем, например, в хорошо известных всем нам сооружениях: высота восьмерика церкви Вознесения в с. Коломенском, от уровня чистого пола до наружного карниза, и высота стен круглого помещения Воскресенского собора Ново-­Иерусалимского монастыря − также от уровня чистого пола до наружного карниза (напомним, что и высоты их шатров равны).

Сажень 142,4 см. Эта сажень не менее популярна в строитель­ной практике; по своей конструкции она представляет собой двух­аршиннуо меру. П.Г. Бутков определил, что именно о ней идет речь в надписи на Тмутараканском камне. «В лето 6576 (1068 г.) индикта 6 Глеб князь мерил море по льду от Тмутаракана до Керчева 10000 и 4000 сажен». Пролив этот П.Г. Бутков со ссылками на другие источники называет в 18⅔ версты и отсюда определяет размер сажени. Пересчитав на наши меры, мо­жем найти, что сажень равнялась:

18⅔ х 1,0668 = 19,9 км,

1 990 000: 14 000 = 142,2 см.

В последующем ряд исследователей древнерусской метроло­гии не соглашались с П. Бутковым (Д.И. Прозоровский, Б.А. Рыбаков). Имелись также и другие толкования надписи.

Разными исследователями сажень 142 см как опровергалась, так и подтверждалась.

Существует мнение, что 142 см сажень является одной из первоначальных мер. Впервые она и само слово «сажень» упо­мянуты в летописном рассказе 1051 г. об отшельнике Иларионе, который «Ископа печерку малу двусаженy и моляшеся ту бу втайне», т. е. выкопал себе пещерку в две «малых» сажени. Г.Я. Романова считает, что слово «сажень» происходит от «сяг» (например, тот же корень в слове «досягать»), от видоизмененного «шаг». «Именно эта мера (сажень, равная удвоенному шагу) применялась князем Глебом при измерении ширины Кер­ченского пролива в 1068 г.» Сажень в 142,4 см согласуется также и с антропометрией, о чем специально скажем в следую­щих разделах.

Сажень 150,8 см. В метрологических исследованиях сажень размером 150-152 см вдруг вновь встречается, будучи вычисленной, по той же надписи на Тмутараканском камне и тому же проливу, о которых только что шла речь. Б.А. Рыбаков, осно­вываясь на сочинении византийского императора Багрянород­ного, называет ширину Керченского пролива в 18 миль и пере­водит их со ссылкой на того же Буткова в 21199 м. Тогда иско­мая величина сажени оказывается 2119900: 14000 = 151,4 см.

Другое упоминание там же со ссылкой на Никоновскую ле­топись о замерах Игнатием Смолянином в 1389 г. в Царьграде окон Софийского собора. Размер назван 2 сажени; современный промер показывает 3 м, откуда сажень приравнивается к 150 см.

Против этого возражает Г.Я. Романова и указывает, что в Никоновскую летопись текст попал с сокращением. В собствен­ном тексте «Хождения» сказано: «Ходихом верху церкве святыа Софиа и видех 40 окон шииных и мерих окно с столпом 2 сажени без дву пядей». В Никоновской летописи не упомя­нуты еще 2 пяди, которые следовало вычесть. Сажень Игнатия Смолянина получается, как считает Романова, примерно 176 см. Б. Рыбаков дает для сажени размером 150-152 см наименование «простая», которое мы далее будем употреблять. Г.Я. Романова подтверждает наличие такого наименования.

В подтверждение функционирования сажени 150-152 см сош­лемся на источник XVII в., на выполненный в XVII в. обмер­ный чертеж Троицкого собора в Пскове. Обмер был составлен по зданию, которое простояло уже 300 лет с момента его возве­дения в XV в. на фундаментах XII в.

После обмера здание было разобрано по причине ветхости и на прежних фундаментах поставлено новое, существующее в настоящее время. Таким образом, помещения сохраняют в основ­ном свои первоначальные размеры, хотя и обрели новые стены. Указанные на чертеже сажени могут быть, поэтому соразмерены с размерами в натуре и приближенно определены их величины.

В таких случаях следует пользоваться наиболее протяжен­ными участками здания. Обычно берется полная внутренняя длина с целью уменьшения возможных расхождений за счет из­менения при последующих перестройках толщин стен.

Согласно записям на чертеже, полная внутренняя длина рав­на 10½ сажени. По современным замерам, это 31,8 м. Откуда размер сажени: 31,8: 10,5 = 3,03 м = 2 х 151,5 см.

Сажень, которой производился обмер, слагалась, как видим, из двух простых.

Чертеж противоречит на первый взгляд принципу Б.А. Ры­бакова об обязательном присутствии в сооружениях нескольких видов саженей; обмер выполнен лишь одним видом сажени. Правда, в нескольких случаях упоминается еще и аршин, не относящийся к системе сдвоенной простой сажени, но, в общем, сажень употреблена лишь одного вида.

Противоречия, однако, нет. Обмерный чертеж - это не твор­ческие разработки зодчего. Обмер выполняется работниками свое­го рода «инвентаризационного бюро». Обмерные чертежи всегда содержат один вид саженей, потому что так удобно мерить. О6­меряльщик никогда и никаким образом не сможет догадаться, какие сажени, сколько их и где применил их зодчий. Характер­ная особенность обмерных чертежей, если они добросовестно исполнены, − наличие дробных величин. Зодчий же обычно мыс­лил целыми величинами, как это было показано на примере Пятницкой церкви в Новгороде.

Поэтому, вопреки распространенному мнению некоторых ис­следователей древнерусской архитектуры и метрологии, старин­ные обмерные чертежи не представляют столь большого интереса для раскрытия «кухни» и методики работы древнерусского зодчего. Даже проектные чертежи, как мы видели выше, не рас­крывают этой кухни; она составляет собой как бы рабочую ста­дию проектирования, выполняемую зодчим и ведущими мастера­ми в процессе строительства, и строго ограничивается этим кру­гом лиц. Иногда лишь частичные сведения сообщаются еще и заказчику. В основном все это относится к профессиональным секретам зодчего и мастеров. Поэтому искать готовые ответы на творческие проработки зодчего в письменных источниках илиобмерах бесполезно.

Для понимания творческих замыслов зодчего сажени, указан­ные на обмерных чертежах, в том числе и древние сажени, нуж­даются в пересчете их на систему тех саженей, которыми мыслил древнерусский зодчий.

Среди саженей зодчего может оказаться и сажень исполни­теля обмеров, так как последний ее брал из того же действовав­шего в древности состава саженей. В нашем примере дробное значение длины здания в 10,5 саженей показывает, что замысел зодчего строился на других саженях. Но не любое дробное число являлось неприемлемым; некоторые из них понимались как це­лые и завершенные, о чем будет свидетельствовать нижеследую­щий пример, где также мы покажем любопытные приемы пропор­ционирования на группе сходных зданий, хотя и разобщенных территориально одно от другого.

Характерные размеры

гpynnы сходных зданий

Строгановские постройки обычно pacсматриваются как группа сходных сооружений. Они относятся к рубежу XVII-XVIII вв. и впечатляют нас виртуозностью и совершенством своих бело­каменных деталей, мастерски сочетающихся с красной кирпичной кладкой. С рассматриваемой нами точки зрения в них достигнуто также мастерство взаимного соразмерения работ двух строитель­ных специальностей − каменщиков и белокаменщиков. Предстает весьма занятная картина при изучении размеров их белокамен­ного декора.

Наиболее известной среди Строгановских построек является Рождественская церковь в Горьком (рис. 2).

Она эффектно расположена и изящно вписана в панораму города, согласуясь с видом на волжские просторы. На фасаде у нее три яруса белокаменного ордерного дeкopa. Высота I яруса − 441 см; II яруса − 498 см; III яруса − 468 см. В сан­тиметрах эти размеры ничего намне говорят; в древнерусских же мерах ярусы соответственно составляют:

I − 2½ сажени народных по 176 см; II − 2½ сажени царских по 197,4 см; III − 2'/₂ сажени церковных по 186,4 см.

Везде по 2½ сажени, но разных видов. Их последователь­ность идет по направлению снизу вверх − народные − царские − церковные. Это весьма характерно, и, по-видимому, здесь ключ к архитектурным пропорциям. Расположения в обратном поряд­ке нам не встречалось.

Смоленская церковь в Гордеевке имеет два таких яруса (рис. 3). Высота I яруса − 610 cм, II яруса − 586 см. В пересчете на древнерусские меры они предстанут в таком виде:

I − 2½ сажени великих по 244 см;

II − 2'/₂ сажени греческих по 230,4 см (с незначительными отклонениями).

Введенский собор в Сольвычегодске (рис. 4),первоначальная строгановская постройка, он также имеет два яруса ордерного декора. Высота ордера: I − 644 см, II − 610 см.

Второй ярус точно такой же по высоте, как первый в смолен­ской церкви − 610 см, и, следовательно, он также имеет 2½ са­жени великих по 244 см. Первый же ярус в сольвычегодской церкви оказывается в величинах, не известных нам по метроло­гичесним источникам. Но нам эта величина хорошо знакома по памятникам древнерусской архитектуры. Ее среднерасчетное значение 258,4 см. Наименования ее мы не знаем. В I ярусе оказывается равной 2½ единицы этой величины, что отвечает общему строю размеров группы церквей.

Носила ли вообще величина 258,4 см наименование сажени? По сравнению с великой саженью (244 см) она является «сверх­саженью», но, если учесть наличие сдвоенных саженей, какие, например, значатся в обмерном чертеже Троицкого собора в Пскове ипревышают 3 м, она не столь уж грандиозна.

И, наконец, Казанская церковь в Устюжне (рис. 5). Как и в предыдущих постройках, в ней два ордерных яруса. Высота I яруса − 640 см, II яруса − 713 см. В первом ярусе вновь та же сверхсажень 258 см, что в сольвычегодской церкви, и вновь в количестве 2½. Второй ярус оказывается равным 2½ саженям, повторенным дважды, т.е. можно считать его равным 5 ма­лым саженям по 142,4 см. Сдвоенные сажени к тому же могли носить и собственные наименования. Сажень близкого размера - 288 см, − указывает Г.Я. Романова, носила название «горо­довой» сажени. Поэтому второй ярус, возможно, представляет собой 2½ сажени городовых по 284,8 см.

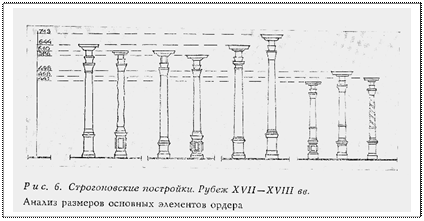
Таким образом, в белокаменном ордерном декоре (рис. 6)в строгановских постройках использована почти полная гамма древнерусских саженей в единой числовой структуре − 2½. Сооружения относятся к одному периоду, хотя и несколько рас­ходятся во времени постройки, к одной школе и сходны между собой по принципам пропорционирования; территориально они значительно разобщены.

Помимо перечисленных саженей и соподчиненных им единиц, существовали еще и другие величины, применявшиеся древнерус­скими зодчими в пропорционировании произведений архитектуры.

Сажень 217,6 см. Ряд башен Коломенского кремля − Возне­сенская, Ямская, Грановитая − указываются размером 17,4 м, что пересчитывается в старинные русские меры как 8 саженей по 217,6 см. Примерно таких же размеров оказывается сажень, показанная на линейном масштабе плана Москвы 1737 г. Это первая инструментальная съемка Москвы, выполнявшаяся главным архитектором города Мичуриным. Нами было произведено соразмерение линейного масштаба мичуринского чертежа с современным планом города. Брались характерные опорные объекты с различным взаимным удалением. Значение сажени колебалось в пределах 216 – 219 см.

Для близкой по значению сажени – 216 см – Б.А. Рыбаков указывает наименование «казенной». Мы применяем его для величины с нашим среднерасчетным значением 217,6 см (что, кстати, не превышает допускаемых отклонений).

Надо сказать, что казенная сажень употреблялась древнерус­скими зодчими в пропорционировании произведений архитектуры меньше других. В последующем казенная сажень была прирав­нена к английским 7 футам и обрела размер 213,36 см, ставший главенствующим в архитектуре XIX в.

В произведениях древнерусской архитектуры встречаются еще величины со среднерасчетными значениями - 134,5, 159,7 и др. Их названия (если только они были) пока не установлены. Ус­ловно мы именуем их «кладочными», так как они входят в состав размеров, хорошо согласующихся с габаритами кирпичной кладки в простенках и столбах.

Следует заметить, что, в отличие от современного кирпича, старинный, большеформатный (30 х 15 см) не был связан жестки­ми размерами с величиной простенков (для современного, напри­мер, требуются размеры 61-64-77-90-103-116-129 см и т.д.). Старинная кладка принимала любые размеры, так как шов не имел постоянной толщины. Но все же и для нее сущест­вовали как более, так и менее рациональные габариты простен­ков. Более подходящим был ряд следующих саженей, полусаже­ней и величин (в среднерасчетных значениях): 108,8 −115,2 − 122 − 134,5 −142,4 −150,8 −159,7.

Между величинами ряда разница около 7−8 см, примерно та­кая же, как между кирпичом полной длины (30 см) и его «трех­четверкой» − 3/4 частью кирпича (23 см), обрубавшейся для перевязки швов и обычно помещаемой по углам.

Мы невольно задаемся вопросом: в чем причина, и какие внутренние силы побуждали зодчих на протяжении многих веков пользоваться одними и теми же величинами, строить части и де­тали сооружений в одних и тех же размерах?

Иногда по поводу методики размерения зданий высказывается уже упоминавшееся нами мнение о якобы изображении на земле схемы абстрактных геометрических фигур, последующем перене­сении размеров с помощью циркульных дуг в каком-то закоди­рованном порядке в третье измерение и получении таким путем размеров на фасадах и разрезах архитектуры. Предшествующий рассмотренный нами материал не подтверждает таких предпо­ложений.

Какова должна быть циркульная засечка, чтобы высоту вось­мерика из с. Коломенского перенести в Новый Иерусалим?

Если функционируют постоянно употребимые величины, то не нужны дуги для их переноса.

Возникает иной вопрос: не в том дело, каким путем размеры попадали в третье измерение, по-видимому, не сложнее, чем в первое и второе, но почему столь устойчивыми они оказались в четвертом измерении − во времени? Какова причина длительного функционирования системы размеров? Если на протяжении мно­гих веков она способствовала созданию прекрасных произведений древнерусской архитектуры, то в чем конкретно состояла эффек­тивность ее воздействий?

Числовые системы пропорционирования

произведений архитектуры

Среди современных методов проектирования и пропорциони­рования зданий существует тенденция к применению определен­ных числовых систем, благодаря чему происходит упрощение процессов проектирования и достигаются большее единство и це­лостность решений. Вводятся различные «модули», стандартизи­руются сетки колонн (6 −12 − 24 − 36 м), производится упорядочение размеров балок, плит и т.д. Существуют специальные госты. В результате в структуре здания создаются четкие по­вторяющиеся ритмы, сокращается число типоразмеров элементов, упрощается строительство.

На протяжении многовековой истории древнерусской архи­тектуры мы встречаем однотипные габариты и размеры злемен­тов, деталей, помещений. Была ли и ранее какая-либо модульная или какая-то иная система, которая благоприятствовала опреде­ленным качествам древнерусской архитектуры? Существование единой стройной системы пропорционирования представляется не­вероятным, но вопрос этот не подвергался всестороннему рас­смотрению.

Б.А. Рыбаков систему древнерусских мер представил как еди­ную целостную систему с определенными закономерностями и ха­рактерными особенностями.

Связывая систему древнерусских мер с потребностями архи­тектуры, Б.А. Рыбаков показал геометрический характер взаимо­зависимостей некоторых мерных величин. В частности, в них сла­гались соотношения сторон и диагоналей квадратов. Графически мерные величины могли изображаться системой вписанных один в другой квадратов.

Такая система мер позволяла объяснить для культовых зда­ний домонгольского периода некоторые разбивочные операции, построение прямых углов, нахождение ряда размеров в наиболее сложной подкупольной части сооружения и по основным его осям. На примере Успенской церкви Елецкого монастыря в Чер­нигове была показана такого рода разбивка.

Однако сооружения последующих периодов − XV − XVI вв. и, особенно, XVII в.− с их развитыми многообразными формами, с целыми каскадами пышных белокаменных деталей, с виртуоз­ными, льющимися, подобно музыке, изгибами линий не могли, естественно, обслуживаться системой величин, привязанных к несложной схеме нескольких квадратов. Системам пропорциони­рования вообще свойственно отражение более общих закономер­ностей, и они не объясняются какой-либо схемой здания, тем более упрощенной.

В этот период, по-видимому, в мерах возникли новые или не­сколько изменились некоторые прежние отношения.

Различные системы, предназначенные для пропорционирова­ния и ускорения архитектурного проектирования, создаются вплоть до настоящего времени; не было препятствий к их функционированию и в прошлом; некоторые из современных находят себе преемственные прообразы в прошлых, несмотря на карди­нальные изменения, произошедшие в современной архитектуре. Укажем, например, на разработки выдающегося французского ар­хитектора Корбюзье. Его система пропорционирования, так на­зываемый «модулор» (в которой, кстати, также делаются попытки увязки с системой мер), при относительно небольшом составе ве­личин способствует достижению в архитектуре эстетически со­вершенных пропорций, обеспечивает многовариантность компо­новок и соразмерение получаемых габаритов с человеком. Вели­чины системы разработаны на основе модели человека. Система Корбюзье обобщила некоторый опыт современной и прошлой за­падноевропейской архитектуры и архитектурной математики.

Однако следует начать с работы знаменитого итальянского математика Леонардо Пизанского (Фибоначчи). В XIII в. он опубликовал числовой ряд, вошедший впоследствии в различ­ные системы пропорционирования.

Этот числовой ряд называется его именем и имеет следую­щий вид:

1−2−3−5−8−13−21−34−55−89−144−233−377 …

Каждый последующий член ряда равен сумме двух предыдущих:

1+2 = 3, 3 + 5 = 8, 8 +13 = 21...

А отношение двух соседних приближается к величине золотого сечения (Ф = 1,618...) особенно по мере увеличения порядковых номеров членов ряда:

5:3 = 1,666; 13: 8 = 1,625; 34: 21 = 1,619; 144: 89 = 1,618...

Золотое сечение известно в архитектуре и изобразительном искусстве с античных времен (возможно, употреблялось и ранее). Наименование «золотое» принадлежит Леонардо да Винчи. Пропорции и отношения, построенные на золотом сечении, обла­дают исключительно высокими эстетическими качествами. Оно свойственно объектам живой природы − растениям, раковинам, различным живым организмам, включая самого человека.

Золотое сечение (его условное обозначение Ф) устанавливает наивысшую соразмерность между целым и частями. Возьмем от­резок и разделим его так, чтобы весь отрезок (а + b) относился к большей части (а), как большая часть (а) − к меньшей (b), т. е.

(a+b) ∕ а = а ∕ b.

Тогда найденное после решения квадратного уравнения отно­шение a ∕ b будет равно величине золотого сечения, выражаемого бесконечной дробью: а/b = Ф = 1,618034...

Соразмерность частей и целого − необходимое условие любого произведения искусства. Лучшие произведения архитектуры всех времен и народов всегда строились соразмерными во всех своих частях, использовали золотое сечение и производные от него функции.

Последовательное деление в золотом отношении может быть продолжено, можно получить ряд величин, подобно ряду чисел Фибоначчи, но, в отличие от него, помимо возрастания, еще и в убывающую сторону.

В восходящую сторону:

1 −1,618... −2,618... −4,236... − 6,854... −11,090...

В нисходящую сторону:

1 −0,618... −0,382... −0,236... − 0,146... −0,090...

Эти ряды называются золотыми геометрическими прогрессия­ми. Знаменателем прогрессии является величина золотого сечения (знаменателем называется число, на которое умножается предыдущий член для получения последующего). В возрастающей про­грессии − знаменатель 1,618...; в убывающей −1∕ 1,618 = 0,618…

3олотые прогрессии - единственные из всех геометрических прогрессий, где последующий член ряда может получаться так же, как и в ряду Фибоначчи, еще и сложением двух предыдущих членов (или вычитанием для убывающей). В отличие от чисел ряда Фибоначчи члены золотой геометрической прогрессии − бесконечные дроби (иногда исключением, как в данном случае, может быть лишь исходный =1).

Итак, несоизмеримые отрезки золотого сечения устанавливают наивысшую соразмерность частей и целого. В ряду Фибоначчи они возникают по мере удаления, когда отношения все более приближаются к золотому сечению.

Характерно и еще одно свойство, общее для рядов Фибоначчи и золотого сечения. Числам этих рядов свойственна многовариантная слагаемость с получением результирующего в их же си­стеме:

3 + 5 = 8,

3 + 5 +13 = 21,

3 + 5 +13 + 34 = 55,

3 + 5 + 5 = 13; 3 + 5 + 5 + 8 = 21 и т. д.

Следует обратить особое внимание на эти комбинаторные свойства чисел ряда. Понимая под комбинаторной ветвь матема­тики, исследующую комбинации и перестановки предметов, мы хотели бы подчеркнуть, что именно благодаря указанной взаимной соразмерности и сопоставимости величин ряда Фибоначчи обеспечивается возможность получения многообразных компоно­вок. Если размеры некоторого ограниченного количества элемен­тов принять в величинах ряда Фибоначчи, то становится воз­можным образование из них более крупных габаритов и форм, взаимно соразмеренных и композиционно совместимых как меж­ду собой, так и в своих частях. Величины ряда Фибоначчи спо­собствуют получению весьма интересных и многовариантных компоновочных решений.

Видимо, поэтому живая природа в своих построениях и ком­поновках часто прибегает к отношениям золотого сечения и вели­чинам этих рядов.

Модулор Корбюзье как математическая система построен на двух рядах Фибоначчи (Корбюзье условно назвал их «линия­ми» − красной и голубой), взаимно соотносящихся между собой путем удвоения. Продолжая начатый пример, покажем схему комбинаторики модулора Корбюзье. Добавим еще ряд удвоенных величин с сохранением условных наименований рядов:

красная линия: 3−5−8−13−21−34−55...;

голубая линия: 4−6−10­−16−26−42−68...

В каждом из рядов существует слагаемость величин, о кото­рой говорилось выше, но, помимо нее, происходит еще и совмест­ная слагаемость величин обоих рядов. Многочисленные вариан­ты сложения можно разбить, например, на такие группы:

1) красные величины в сумме дают голубую: 3 + 5 + 13 + 21 = 42,

2) красные и голубые в сумме дают красную: 3 + 10 + 42 = 55,

3) красные и голубые в сумме дают голубую: 3 + 5 + 8 + 26 = 42,

4) красные и голубые, взятые по несколько раз, в сумме дают голубую:

2 х 5 + 2 х 16 = 42,

5) то же, но красную: 1 х 4 + 2 х 6 + 3 х 13 = 55 и т.д.

Этим далеко не исчерпываются возможные варианты. Коли­чество величин в системе хотя и удвоилось, но комбинаторика возросла многократно как в абсолютном значении, так и в отно­сительном (в расчете количества вариантов на 1 величину).

Небольшое количество величин позволило получать весьма много разнообразных компоновок.

Построив с использованием модулора всемирно известный дом в Марселе, Корбюзье писал: «Я дал задание проектировщикам мастерской составить номенклатуру всех использованных в здании размерных величин. Оказалось, что пятнадцати размерных величин было вполне достаточно. Всего пятнадцать!». Это весьма и весьма показательно. Правда, в названном количестве не учтены, видимо, суммарные, дробные и другие виды размеров; а лишь модулорные, но и они дают представление о высоких воз­можностях комбинирования с помощью системы «модулор».

Все величины модулора были увязаны с моделью человека. За исходные параметры модели Корбюзье принял рост, равный 6 футов = 183 cм, и размер в положении с поднятой рукой = 226 см. От исходных величин по математическим закономерностям чисел Фибоначчи Корбюзье вычислил все остальные и получил в сан­тиметрах:

красная линия: 16−27−43−70−113−183...

голубая линия: 20−33−53−86−140−226...

На рисунках, выполненных Корбюзье, показывалось, как эти ве­личины согласуются с размерами и положениями тела человека. 3а создание системы «модулор» Корбюзье получил патент и всемирное признание.

Укажем на некоторые распространенные виды пропорций, ко­торые строятся величинами модулора:

Ф = 1,618... 2/ Ф = 1,236... Ф ²/2 = 1,309... 2/ Ф ² = 0,472...

Последнее отношение представляет собой одну из так называе­мых «функций Жолтовского».

И.В. Жолтовскому, выдающемуся зодчему современности, назначенному еще в первые годы Советской власти при В.И. Ленине главным архитектором Москвы, принадлежит научное обоснование и практическое внедрение в современную прак­тику эстетически наиболее ценных и изысканных пропорций в архитектуре, производных от золотого сечения. Он выявил их, исследуя лучшие произведения античности и ренессанса, точно рассчитал и применял в современной архитектуре. В частности, И.В. Жолтовский при анализе пропорции Парфенона в отноше­ниях между диаметром колонны и интерколумнием, между высо­той антаблемента и фронтона указывает отношение, составляю­щее в числовом выражении 528: 472. Чтобы получить малый отрезок, характеризующий это отношение, Жолтовский в убы­вающем ряде золотой геометрической прогрессии берет значение третьего порядка − 0,236, удваивает его и получает 0,472. Вы­читание этой величины из единицы дает 0,528. Отношение 528: 472 было названо «функцией Жолтовского».

Учитывая, что в древнерусской архитектуре встречается очень много отношений, как по функции Жолтовского, так и по отдель­ным ее составляющим, мы ввели в целях удобства изложения материала, следующие условные наименования, которыми ниже 6yдем пользоваться:

0,472 − первая составляющая функции Жолтовского, или со­кращенно − первая функция Жолтовского с условным обозначением Fж₁

0,528 − вторая составляющая функции Жолтовского, или со­кращенно − вторая функция Жолтовского с условным обозначением Fж₂.

0,528: 0,472 = 1,118...− основная функция Жолтовского, или функция Жолтовского с условным обозначением Fж.

Дата добавления: 2014-12-07