Гармония золотых пропорций 8 страница

Следует отметить, что корень двенадцатой степени из 2 появился не случайно. Он следствие перенесения на базисный столбец рациональных чисел отображающих деление динамического отрезка на 12 физически одинаковых частей. То есть здесь имеет место почисловое отражение русского ряда на вертикальный базисный ряд матрицы.

В матрице 6 древнерусские сажени располагаются, начиная с 350-й строки, под базисной 1 и заканчиваются 418 строкой. А по столбцам начиная с 60-й и заканчивая 70 столбцом [23]. Отмечу, что величина саженей подобрана таким образом, что получается ступенчатая последовательность расположения значащих чисел (их длин с точностью до четвертого знака), которая обеспечивает, посредством 12 последовательных умножений на 1,05946, удвоение каждого числа. Это очень удивительная структура, определяющая некую «иерархически соподчиненную» взаимосвязь чисел матрицы

6. В ней величина длин саженей оказывалась «выше» по значимости, чем расположенные под ними 10 «промежуточных» чисел. Эти промежуточные числа в столбцах можно «убрать», проведя операцию «свертывания» промежуточных чисел и подтягивания в одну строку оставшихся значащих чисел. Последнее не меняя структуру матрицы, увеличивает шаг базисного столбца и изменяет ее числовое поле, а, следовательно, и ранг чисел, переводя их из «соподчиненных» в смежные, убирая физическую гармонику базисного ряда, а с ним «укрывая» и качественную обусловленность взаимосвязи всех физических свойств.

Матрица 6

0,1670	0,2550	0,3895	0,5949	0,9085	1,387	2,119	3,236	4,942
0,1576	0,2407	0,3676	0,5615	0,8575	1,309	2,000	3,054	4,665
0,1488	0,2272	0,3470	0,5300	0,8094	1,236	1,888	2,883	4,403
0,1404	0,2146	0,3275	0,5002	0,7639	1,167	1,782	2,721	4,156
0,1325	0,2024	0,3091	0,4721	0,7211	1,101	1,682	2,568	3,923
0,1251	0,1911	0,2918	0,4456	0,6806	1,039	1,587	2,424	3,703
0,1181	0,1804	0,2754	0,4296	0,6324	0,981	1,498	2,288	3,496
0,1114	0,1702	0,2599	0,3970	0,6063	0,926	1,414	2,160	3,296
0,1052	0,1607	0,2464	0,3747	0,5723	0,874	1,335	2,039	3,113
0,0993	0,1516	0,2316	0,3537	0,5402	0,825	1,260	1,924	2,939
0,0937	0,1431	0,2186	0,3339	0,5099	0,779	1,189	1,816	2,774
0,0885	0,1361	0,2063	0,3151	0,4812	0,736	1,122	1,714	2,618
0,0835	0,1275	0,1948	0,2974	0,4542	0,694	1,059	1,618	2,471
0,0788	0,1204	0,1838	0,2807	0,4282	0,655	1,000	1,527	2,332
0,0744	0,1136	0,1735	0,2650	0,4047	0,618	0,944	1,441	2,201

Выбор размеров древнерусских саженей оказался далеко не случайным, хотя таким он кажется на первый взгляд. Если, начиная с 1 сосчитать количество строк - 351 до численного размера наименьшей из саженей – 1,345 м. и, возвести основание 1,05946... в степень 351, то получим, с точностью до 0,1% модуль радиуса земного шара – 6384,5 км. Более точное целое число получается, если разделить радиус Земли, равный 6378 км, на длину царской сажени 1,974 м или на ту же меньшую сажень 1,345 м. Результат поразителен для чисел из четырех значащих цифр. Получаем целые до шестого знака числа: 323100 в первом случае и 474200. Эта интересная «случайность» обусловливает объектам, возводимым по древней методике получение объемов сооружений, квантованных пропорционально структуре Земли (подробнее [23]).

И, наконец, еще одна важная для понимания естественной структуры реального пространства особенность формы русской матрицы. Из всех клеток-ячеек матрицы уберем числа, оставив только базисную 1, проведем нумерацию их, начиная с этой 1, и поставим в верхнюю клетку цифру 2. Далее двигаясь по часовой стрелке, получим удивительную и странную полуматрицу (матрица 7), сводящую динамическую геометрию с геометрией золотых пропорций и отображающую их квантованное единство.

Рассмотрим фрагмент этой полуматрицы из 121-й клетки-ячейки.

Матрица 7.

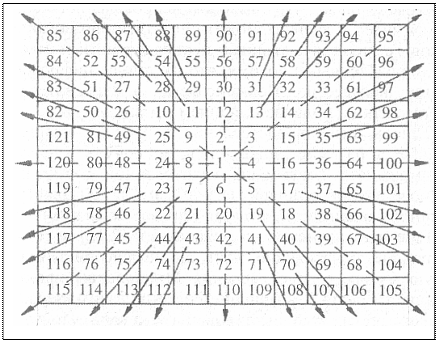Образующаяся полуматрица интересна сама по себе и заслуживает отдельного исследования. Таблица названа полуматрицей, поскольку в нее входят и взаимосвязанные и степенные числа, изменяющиеся на одну и ту же величину.

Всеобщая связь между каждым числом, похоже, отсутствует. Например, все клетки базисного «креста» горизонтального и вертикального слоев заполнены четными числами, что свидетельствует о качественном отличии базисной 1 от других чисел матрицы. Но главное достоинство полуматрицы в том, что на ее примере можно наглядно демонстрировать образование лучей-спиц, но не снаружи внутри, как на рис. 33, а изнутри наружу. Иначе говоря, структура этих двух моделей аналогична. И аналогия эта, во-первых, подтверждает единство геометрий, а во-вторых, позволяет проследить процесс образования ячеистой системы лучеиспускания на плоскости. Процесс сохраняется и при построении объемной ячеистой структуры (в ней клетки превращаются в кубики-ячейки).

Итак, первые четыре луча 2-90; 4-100; 6-110; 8-120 исходят от границ базисной ячейки и образуют крест. В своем движении наружу они «засвечивают» все встречающиеся ячейки. Следующие четыре луча (9-85; 3-95; 5-105; 7-115) исходящие из центров нечетных ячеек, «засвечивают» все диагональные ячейки, образуя диагональный крест. Далее количество ячеек удваивается, и лучи испускают ячейки 11, 13, 15, 17, 19, 21, 23, 25. Эти ячейки с нечетной нумерацией по очертанию начинают приближаться к окружности, образуя фигуру наподобие кольца (сферы в объеме). Испускаемые ими лучи двигаются наружу как бы от центра базиса «засвечивая» ячейки через одну. Лучи исходят из смежных, относительно центральной единицы, ячеек в противоположных направлениях. Например, луч из ячейки 11, пропуская одно кольцо ячеек, «засвечивает» 54, далее 129 и т.д. Противоположный луч из ячейки 19 через ячейку 70, 153 и т.д.

При переходе от плоской матрицы к объемной, эффект сферы лучеиспускания усиливается и с каждым новым слоем ячеек объем сферы возрастает, а плотность исходящих лучей превращается в некоторый аналог «ежика» следов, входящих в сферу как на рис. 33.

Уже говорилось,что символом непроявленного «движения» чисел в ячейках может считаться образование числового поля в матрицах неопределенными числами. Неопределенными потому, что их точное цифровое значение неизвестно. Невычисляемо, а следовательно, и непостоянно, подвижно, причем самоподвижно.

Теперь, имея представление о русских матрицах и опираясь на их числовые поля, попробуем рассмотреть возможность построения квантованной физической геометрии на основе числовых полей матриц 2 и 4 и той пространственной зависимости, которая скрывается за ними.

Еще раз вернемся к уравнению (3.12) и отметим странное заблуждение, чуть ли не эйфорию, охватившую ученых после введения Минковским времени и скорости света в уравнение системы взаимнопересекающихся плоскостей евклидовой геометрии. Получившемуся квадратичному уравнению

0 = c² t² − x² − y² − z², (5.6 )

качественно не изменившему евклидовости пространства, поскольку в квадратичном уравнении Евклида один размерный индекс был заменен на другой и только, Минковский, без каких либо оснований, приписал ранг четвертого измерения. То есть нового качественного состояния - четырехмерной объемности, а, следовательно, и неевклидовости.

И, как это ни удивительно, но сначала физики, а затем и математики поверили в «четырехмерность» полученного квадратичного уравнения и, более того, стали получать аналогичные «пятимерные» (Калуца), «шестимерные»..., «одинадцатимерные»..., «двадцатипяти...» [33] и т.д. мерные квадратичные уравнения. Как то забылось, что х ² - есть плоскость (не объем), разделяющая (а не образующая) пространство на две части, а координата х - след-линия пересечения этой плоскости с другой ортогональной ей, у ² - тоже плоскость, но в ином ортогональном направлении. И, наконец, z ² - такая же плоскость, ортогональная двум другим. И объем не образуется этими тремя взаимнонезависимыми, не связанными между собой плоскостями, а заключается между ними. И в этом объеме с ² t ² - еще одна плоскость, проходящая ортогонально одной из них в стык двух других.

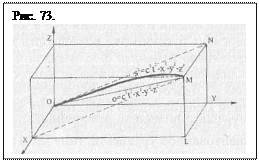
Введение в уравнение (3.9) неравенства и дополнительной координаты s не меняет качества уравнения, поскольку s ² - тоже плоскость неопределенной ортогональности. или искривленная линия, если считать, что (5.6) аналог (3.12) С появлением этой индексации в евклидовой геометрии не изменилось ничего, кроме названия. Модель решения уравнения (3.12) получена Ф. Канаревым [34] и показана на рисунке 47, на котором путь от О к М отмечен и по уравнению (3.11) и по уравнению (5.6). Разница понятна и без пояснения.

Что касается с ²× t ², то его появление в уравнении (3.12) нарушило пространственную соразмерность параметров х, у, z и потому превратило однозначность решения уравнения Пифагора в многозначность даже без учета того, что время как естественная категория в природе отсутствует [2], к тому же плотность евклидова пространства изотропна, а матричного пространства - анизотропна. Именно «выпрямляя» анизотропность, искривляют пространство члены уравнения (3.12) в «знаменитой» теории ОТО. И из решения уравнения (3.12) могут быть получены как корректные (случайно), так и полностью некорректные (регулярно) результаты.

Но элементы псевдо-евклидовой геометрии русского ряда золотой пропорции (3.9) совер- шенно иначе «реагируют» на введение других членов. Они не могут содержать «лишних» членов и форма неравенства (3.10¢) для них невозможна. Неравенство предполагает расширение количества членов, а ряд такого расширения не допускает. Поэтому неравенство (3.10¢) «выводит» взаимосвязи между членами (3.10) за рамки отдельного ряда в плоскость матрицы, когда у_о оказывается не равной z: у_о ¹ z, допуская введение в (3.10) новых членов, первым из которых и становится s².

Таким образом, заменив равенство в (3.10) на неравенство и введя равноправный член s ² в уравнение (3.12), математики не в евклидовой, а в квантованной геометрии произвели не одно действие, а два (так же как и при делении в крайнем и среднем отношении). Превратили «самостоятельный» ряд в диагональ матрицы 1 переведя русский ряд в плоскость матрицы. Качественно изменив, таким образом, форму связи членов уравнения (3.9) с линейной, между членами одного ряда, на плоскостную − между числами поля всей матрицы, но не изменив квантованного характера их зависимости.

Построим, базируясь на поле матрицы 3, численное квантованное уравнение типа (3.11). Для этого, методом матричной «вязи» найдем такую комбинацию чисел, которая соответствовала бы равенству n ² = 1² − s ². Естественно, что число 1, в данном случае, не является базисным:

0,618 = 1,618 - 0,472 - 0,382 - 0,146. (5.7)

Если числа уравнения (3.14) записать в степенной форме, то оно станет некоторым подобием уравнения (3.12):

(0,786) ² = (1,272) ² - (0,687) ² - (0,618) ² - (0,382)².

В индексах уравнения (5.7) и (3.12) - полные аналоги и представляют собой трехмерное пространство, поделенное плоскостями. Но уравнение (3.12) отображает непрерывное, изотропное евклидово пространство, рассеченное плоскостями и не имеющее выделенных точек, а (5.7) отображает квантованное пространство, состоящее из выделенных точек, - анизотропное пространство, точки которого хотя и связаны с другими точками своими свойствами, но индивидуальны по количественной величине этих свойств. Наличие с ² t ² в уравнении (3.12) не изменяет качества статического, изотропного евклидова пространства.

- Из (3.9) и (5.7) следует, что оба уравнения отображают строго определенные точки числовой матрицы, но (3.9) - линейное построение точек, а (5.7) - пространственное.

- И в том и в другом случае имеет место принадлежность как минимум трех числовых точек х, у, z линейной структуре, что позволяет видеть за ними трехчастное членение числового поля матрицы у.

- Переход от линейного уравнения (3.9) к плоскостному (5.7), сопровождается качественным скачком, и можно ожидать аналогичного скачка и при переходе от плоскостного к объемному.

- Переход от статической к квантованной динамической геометрии характеризуется появлением в математической формализации категории качества, что еще раз свидетельствует о принадлежности динамической геометрии к физике.

Уравнение (5.7) характерно для динамического пространства изменяемой метричности, т.е. по смыслу противоположного евклидову и потому за ним можно сохранить название псевдоевклидово пространство.

Таким образом, введение неравенства (3.10) не приводит к получению четырехмерного пространства, а только изменяет форму вычисления точек в евклидовом трехмерном пространстве. Да и не может изотропное пространство, по определению, иметь измерений больше трех, поскольку увеличение мерности автоматически предполагает появление нового качества и, следовательно, нарушение изотропности хотя бы в одной точке пространства. По евклидовой геометрии это просто не допустимо. Но динамическая псевдоевклидова геометрия, квантованная индивидуальными точками, и отображает анизотропное пространство.

Приведем некоторые соображения, связанные с золотыми пропорциями:

По-видимому, множество золотых сечений - пропорция иррациональных чисел, разделяющих объемные параметры фигур соответственно изменению пространственной мерности. Они отражают природную соразмерность соответствующих структур, взаимосвязей и взаимодействий реального мира. Они отображают гармоническую последовательность деформации материи при образовании кристаллических структур и структурирование тканей при росте и развитии живых организмов. Конструкции, нарушающие золотые пропорции, не совместимы с природными процессами, вносят возмущение в их течение, а потому обладают предрасположением к ускоренному разрушению.

Абстрактная единица в золотом многообразии отсутствует. Но ее условный символ - базис, - воспринимается нами как абстракция. Ряд иррациональных многомерностей бесконечен и внутрь и наружу. Он охватывает иррациональную Вселенную, но, по-видимому, не затрагивает рациональный мир (мир рациональных чисел), причем, похоже, иррациональными являются и простые числа, и их произведения. Важно не то, сколько чисел составляют золотой ряд, а какова их темперация, такт и лад.

Числа золотого многообразия - безразмерностные коэффициенты, отображающие пространственное изменение качества. Они «работают», по-видимому, только тогда, когда имеется «эталонный» модуль - первое от базисной 1 число, определяющий процесс восхождения или нисхождения ряда. Модуль - как бы является коэффициентом «приращения» мерности пространства, ее родственности этому пространству. Числа золотого сечения - «стержни» этого движения, придающие стабильность происходящим процессам.

Условная базисная единица символизирует постоянный переход, постоянное движение пространства в своей окрестности, и поэтому она никогда не может быть абстрактной. Представление ее как абстракции переводит математику иррациональную – динамическую в математику рациональную – статическую. Именно на абстрактной единице построена вся современная математика, которая поэтому не может адекватно описывать природные процессы.

Отбросив условности и превратив единицу в абстракцию, люди тем самым отбросили незаконченные переходные процессы, которые относятся как к развитию человека, так и к развитию любой области природы.

Отбросив переходные процессы, человечество ввергло себя в хаос технократии, включило механизм регрессивного движения к изначальному состоянию (буквально - в пещеры), к состоянию, определяемому выражением «конец света».

Существование чисел золотого многообразия, их связь с параметром p, а следовательно, со строением реального мира, обусловливает иное понимание структуры окружающего пространства и его мерности. Об этом же свидетельствует и структура квантованной динамической геометрии, базирующейся на золотых пропорциях и анизотропность окружающего пространства.

Три координаты евклидова пространства, проходящие через О, есть «свернутая» аналогия деления объема плоскостями. Они «закрывают» евклидову ортогональность, закрывают одно качественное состояние «равноуплотненного» пространства. Наращивание координат - наращивание количества плоскостей - не изменяет пространственной плотности и не открывает новой мерности, поскольку оставляет ей квадратичную (плоскостную) структуру. Только изменение представления об объемности и координатности (количество координат в уравнении равно их степени) изменяет понимание о пространстве как о длине в разных направлениях, на представление плотности пространства как перехода к новому качественному состоянию, как отображение условий существования реального пространства. Некоторое возможности такого наращивания, и построения n -мерного пространства рассматривается в следующем разделе.

5.3. Введение в плотностную r_n -мерность

Пространственное расположение фигур и расстояния между ними описываются в современной геометрии в основном методами координат, и в частности декартовых. Три взаимно ортогональные координатные оси обусловливают возможность привязки к их пересечению всех точек пространства. Метод базируется на постулировании независимости и равнозначности каждой координатной оси, а их общее количество как бы отображает трехмерность реального пространства. И остается под вопросом возможность существования большего количества мерностей. Однако, как уже упоминалось, это не мешает математикам оперировать с любым количеством мерностей. Основа этих п-мерных операций заложена в постулате Римана о многократно протяженных величинах. Им, вслед за Декартом, постулируется, что все координатные оси равнозначны и каждое сверхтрехмерное измерение является самостоятельной мерностью, не связанной ни со свойствами пространства, ни со свойствами тел.

Но природа едина, свойства ее взаимосвязаны, она не излишествует свойствами, обладающими «свободной волей», и поэтому надо искать в отображениях ее образований подсказку того, как и в чем проявляет себя пространственная n -мерность. За геометрической подсказкой снова обратимся к евклидовой геометрии.

Одной из наиболее известных теорем этой геометрии, как неоднократно подчеркивалось, является теорема Пифагора. В ней утверждается, что:

«Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов».

Это знали еще древние египтяне, а священный прямоугольный треугольник со сторонами численно равными 3, 4 и 5, служил основой построения прямого угла на плоскости и носит название священного египетского треугольника.

Теорема проста, и ее изучение в школе сопровождается иллюстративным доказательством справедливости посредством построения на каждой стороне треугольника квадрата. Если же площади квадратов сложить, то они оказываются равными площади квадрата гипотенузы:

a ² + b ² = c ². (5.8)

В аналитической геометрии уравнение (5.8), путем деления левой части на правую часть, превращается в уравнение окружности на плоскости:

a ²/ c ² + b ²/ c ² = 1. (5.9)

Особенность уравнения (5.8) в том, что подстановка в его левую часть вместо индексов а и b квадратов последовательности чисел а = 3 и b = 4 приводит к получению квадрата следующего числа натурального ряда с = 5. Существует еще одно аналогичное (5.8) суммирование, но уже не квадратов сторон, аих кубов:

a³ + b³ + c³ = d³. (5.10 )

И в этом уравнении сумма кубов, построенных на длинах последовательного числового ряда египетского треугольника а = 3; b = 4; с = 5, равна кубу длины следующего числа ряда - 6. Поскольку кубы образуются на базе метрического числового ряда, то сумма их, равная кубу последующего числа, смотрится как некоторая случайность. Но два уравнения, подчиняющиеся одинаковой последовательности (5.9) и (5.10), образоваться случайно уже не могут. Они - следствие непознанной закономерности.

Логика геометрических построений подсказывает, что на этом ряд степенного суммирования не заканчивается и следует ожидать его продолжения добавлением к уравнению (5.10) очередной цифры числового ряда, а к показателю степени - очередной единицы.

a⁴ + b⁴ + c⁴ + d⁴ = e⁴ (5.11 )

Но, увы, левая сумма неравенства (5.11) не равна четвертой степени очередного числа. И на этом степенная последовательность уравнений как бы прерывается. Однако остается вопрос: почему она прерывается? Вопрос важен и потому, что со временем уравнение (5.8) стало геометрическим аналогом двумерного пространства, а подобное ему по структуре уравнение (5.10) аналогом трехмерного пространства. И не может ли неравенство (5.11) оказаться некоторым аналогом пространства четырехмерного?

Рассмотрим этот проблематичный ряд несколько с иной позиции. Уравнение (5.9) подсказывает, что в египетском треугольнике может быть зашифрована не сумма квадратов катетов, а сумма площадей некоторых окружностей, имеющих радиусом модуль чисел египетского треугольника. И это достаточно просто показать, превратив уравнение (5.8) из суммы площадей квадратов в сумму площадей окружностей, добавив в качестве сомножителя каждого члена p:

pa ² + pb ² = pc ² (5.12 )

Становится ясным то, что сумма квадратов площадей (5.8) была получена так же, как и третий закон Кеплера, посредством сокращения всех членов уравнения (5.12) на общий для них коэффициент p. Результатом сокращения стало изменение смыслового значения самого уравнения. Иррациональная площадь одних фигур - кругов оказалась подменена рациональными площадями других фигур - прямоугольных треугольников. (Очередной пример изменения качественной значимости уравнения при сокращении всех его членов на иррациональный коэффициент.)

Однако в (5.12) p не коэффициент пропорциональности радиуса и окружности. p - это их соизмеримость. И в (5.12) складываются не площади. Сложение плоскостей и объемов r_п - мерностей есть сложение иррациональных степенных отображений свойств. Есть соизмерение несоизмеримого. Соизмеримость новое качество, элемент бесконечности и поэтому складываются степенные образования, а сложение оказывается элементом неопределенности. И поэтому сокращение на p в принципе невозможно ни в одной математической операции, поскольку сопровождается качественным изменением смысла уравнения, неявным превращением иррационального в рациональное .Отсюда следует, чтоуравнение (5.8) качественно отличается от уравнения (5.12).Например, иррациональная неопределенность отсутствует у площадей многоугольников и их можно складывать в любых операциях. Сложение таких площадей не сопровождается появлением иррациональностей (конечно, если стороны многоугольников не иррациональны). При сложении площадей кругов или объемов шаров наличие иррациональности неизбежно как следствие иррационального качества соизмеримостей.

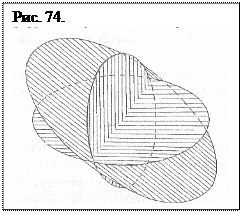Из (5.12) следует, что в действительности складываются площади, но не треугольников, а двумерных окружностей. И сумма двух площадей, образуемых радиусами числовой последовательности 3, 4, составляет площадь окружности с радиусом 5. Если считать, что стороны египетского треугольника являются радиусами некоторых окружностей, то на их базе можно построить три взаимно пересекающиеся окружности. Нарис.74 приведен один из вариантов такого построения. Взаимное расположение окружностей по координатным осям как бы показывает, что метричность двумерного пространства не меняется при любом положении окружностей в нем. Эту неизменность и демонстрирует равенство суммы площадей двух меньших окружностей - большей. Именно этот результат заставляет предположить, что формула (5.10) описывает аналогичное сложение объемов.

Переходя теперь к уравнению (5.10), следует отметить, что и его достаточно просто можно превратить в сумму, но уже не площадей окружностей, а объемов сфер-шаров на базе радиусов того же последовательного ряда чисел умножением каждого члена уравнения на коэффициент 4/3p:

4/3 pa³ + 4/3 pb³ + 4/3 pc³ = 4/3 pd³. (5.13)

И здесь, аналогичным сокращением на 4∕3 p из шаров численно неопределенного объема были получены численно определенные кубы (5.10), которые окончательно скрыли зависимость количественной величины p от мерности, а, следовательно, и плотности получаемой геометрической фигуры. Уравнение (5.13), хотя и аналогично уравнению (5.10) по структуре и как бы следует из него, являет совершенно иной физический смысл. Оно показывает, что в трехмерном пространстве три радиуса любой области одной как бы рациональной числовой последовательности а, b, с, образуют сферы-шары, суммарный объем которых равен объему четвертой сферы - шару с радиусом d из той же числовой последовательности.

Таким образом, последовательность уравнений (5.12) и (5.13) демонстрирует некоторую однородность и изотропность двумерной и трехмерной части пространства. И эта однородность прерывается на неравенстве (5.11) либо потому, что мир трехмерен, либо потому, что переход в более высокие измерения сопровождается изменением плотностной метричности пространства, а, следовательно, и изменением численной величины коэффициента p. В этом случае уравнение числовой последовательности (5.13) запишется следующим образом:

4/3 pa⁴ + 4/3 pb⁴ + 4/3 pc⁴ + 4/3 pd⁴ = 4/3 p_ee⁴. (5.14)

Если считать, что каждое слагаемое имеет собственное числовое значение, соответствующее п -мерности, то логика последовательности может быть показана построением пространственного мерного ряда уравнений (Таблица 6).

Предположим, что:

а - индекс какого-то числа натурального ряда или абстрактное числовое обозначение длины, не связанной с плотностной мерностью;

а ¹ - длина одномерного луча;

aⁿ, bⁿ, cⁿ, l,…, kⁿ - длины лучей, у которых показатель степени

соответствует мерности пространства.

Таблица 6

Мерность пространства	Уравнения
Безмерностное	a
Одномерное	a ^1 = b ^1
Двумерное	a ^2 + b ^2 = c ^2
Трехмерное	a ^3 + b ^3 + c ^3 = d ^3	(5.15)
Четырехмерное	a ^4 + b ^4 + c ^4 + d ^4 = e ^4
Пятимерное	a ^5 + b ^5 + c ^5 + d ^5 + e ^5 = f ^5
...............	........................
n - мерное	a^n + b^n+ c^n +... + k^n = l^n

Дата добавления: 2014-12-07