Гармония золотых пропорций 4 страница

Проведем базисную прямую и из точки О, как из центра радиусом R = 5 см и опишем полуокружность АВ. Из центра полуокружности и из точек А и В восстановим перпендикуляры. Получим тройку параллельных прямых Евклида. Примем, что средняя прямая – поляра, а точка О есть одновременно точка N, и на любой высоте от базиса, например, на высоте 28 см, поставим на поляре несобственную точку S,

в которой пересекаются две параллельные Дезарга. Через точку пересечения поляры и окружности проведем касательную до пересечения со сторонами АS и SВ в точках С _о и Д _о, получим крышу – верхнее основание трапеций АС _о Д _о В. Соединив эти точки с точками А и В убедимся, что диагонали АД _о и ВС _о пересекаются на поляре. Через точку пересечения поляры с прямой С _о Д _о проведем еще две диагонали АД, ВС, и, соединив их прямой СД, имеем трапецию АСДВ и т.д. Процесс построения трапеций в пирамиде бесконечен как к точке S, так и к базисной прямой, поскольку точка опоры S, как и базисная прямая недостижимы. Между ними и ближайшими к ним крышами всегда остается опорный или базисный промежуток возрастающей плотности. Мы ограничимся построением крыши С ₄ Д ₄, и для выявления пропорциональности высот между крышами, спустимся аналогичным образом еще на крышу ближе к базисной прямой проведя прямую С _к Д _к.

Отметим главное отличие в пространстве проективной геометрии от плотностного пространства статико-динамической, ярко проявляющееся в этом построении. Чем ближе к точке S находятся крыши пирамид, тем меньше расстояние между ними. То же самое происходит и с крышами, «приближающимися» к базисной прямой. Чем ближе они к ней, тем меньше расстояние между ними. И данное построение можно продолжать бесконечно. Именно это обстоятельство свидетельствует об изменении плотности пространства между точкой опоры S и базисной прямой таким образом, что где-то между ними должна существовать нейтральная зона одинаковой плотности пространства. Убедимся в этом, замерив, расстояние между крышами. Оно оказывается снизу вверх равным в см: 2,3; 3,5; 4,5; 4,8; 3,9; 2,8 … и т.д. Максимальное расстояние наличествует между третьей и четвертой крышами. Оно и свидетельствует о том, что в данной области пространство имеет наименьшую плотность. Неравенство расстояний между крышами, например, в статической геометрии предполагает диспропорциональность этих расстояний. Однако проверка пропорциональности вурфным методом W (а, b, с) по уравнению:

W (а,b,с) = (а + b)(b + с) ⁄b(а + b + с) (4.2)

W ₁ = (2,3 + 3,5)(3,5 + 4,5) ⁄ 3,5(2,3 + 3,5 + 4,5) = 1,287

W ₂ = (3,5 + 4,5)(4,5 + 4,8) ⁄ 4,5(3,5 + 4,5 + 4,8) = 1,292;

W ₃ = 1,277; W ₄ = 1,299,

с точностью до третьего знака доказывает ее наличие. Это свидетельствует о том, что имеет место не геометрическое неравенство, а физическое равенство расстояний между крышами. (Базисный ряд русской матрицы). Это обстоятельство и определяет форму пропорционирования фигур статико-динамической геометрии. Для пропорционирования используется не двучастное деление пропорционируемых отрезков, а трехчастное. Пропорционируется не численная величина двух расстояний, а величина трех соседних отрезков.

Убедившись в наличии пропорциональности высот трапеций с параллельными крышами, построим трапеции с наклонными крышами соединив прямыми, например, точку С ₄ с точкой Д ₃, точку С ₃ с точкой Д ₂ и т.д., и продолжим лучи от наклоненных крыш до пересечения с базисной прямой (рис. 59). Лучи всех крыш оказываются в одной точке М, которая для симметричных пирамид всегда отстоит от точки В ровно на длину диаметра, и таким образом пропорция (4.1) оказывается сохраненной.

Увеличим наклон крыш соединив точку С ₄ с точкой Д ₂, точку С ₃ с точкой Д ₁ и т.д. и продолжим их лучи до пересечения с базисной прямой (лучи к базису на рис. 59.). На ней появляется новая гармоническая точка М ₁, отсекающая ровно 1 ⁄ 3 длины ВМ. Все больше и больше увеличивая наклон крыш, получаем фиксированные гармонические точки серии М ₂, М ₃, М ₄ и т.д. Естественно, что теперь пропорция (4.1) между отрезками диаметра и точкой М ₁ не будет соблюдаться:

АN ⁄ NВ ≠ АМ ₁ ⁄ М ₁ В,

поскольку изменилось расстояние до М ₁ и для появления новой пропорции должно измениться местонахождение точки N.

Для получения месторасположения точек серии N необходимо одновременно с увеличением, например, наклона крыш с С ₄ на Д ₂ проводить лучи из точки С ₄ через середину крыши С ₂ Д ₂, до пересечения с базисной прямой, что обусловливает получение гармонической точки N ₁, Точка N ₁ отсекает ровно 1 ⁄ 3 диаметра и уравнение (4.1) сохраняет свой вид в следующей форме:

АN₁ ⁄ N₁В = АМ₁ ⁄ М₁В (4.3)

Для сохранения пропорций каждой гармонической точки серии М: М ₂, М ₃, М ₄ и т.д. аналогичным образом из точки С ₄ через середину крыши С ₁ Д ₁, СД, С_оД_о и т.д. проводятся прямые до пересечения с базисной прямой в точках N₂, N ₃, N ₄ и т.д. Эту серию гармонических точек можно назвать спутницами поляры N.

Естественно, что между каждой из крыш можно построить множество других взаимосвязанных наклонных крыш, получая такое же множество новых фиксированных гармонических точек на базисной прямой. При построении точек, аналогов точкам серии М, слева от пирамиды, симметрично вырисовывается та же картина их расположения на базисе.

Определив расположение множества гармонических точек, рассмотрим, какие изменения произойдут при перемещении точки опоры S пирамиды по высоте, например, в точку S _о на поляре с уменьшением по высоте, или в точку опоры S ₁ с отклонением по вертикали вправо. Поскольку все параметры серий точек М и N от пирамиды с точкой S _о на поляре, уменьшенной по высоте, аналогичны параметрам высокой пирамиды, остановимся на последнем варианте и построим (штрихованную) наклонную пирамиду с точкой опоры S ₁. Проведем, через точку пересечения полярой окружности, диагонали первой трапеции и, аналогично предыдущему, построим семь этажей крыш. Хотя пирамида деформировалась и наклонилась, крыши, тоже деформировавшись, как и все элементы пирамиды, сохранили горизонтальное положение. Это свидетельствует о том, что в горизонтальном направлении плотность пространства между точкой опоры и базисной прямой не изменяется по горизонтали.

Построим наклоненные крыши, соединив прямыми С ₄´ Д ₃´, С ₃´ Д ₂´, С ₂´ Д ₁´ и т.д., и продолжим лучи от них до пересечения с базисной прямой. Лучи всех крыш сойдутся в точке М. Соединим углы крыш через этаж С ₄´ Д ₂´, С ₃´ Д ₁´, и т.д. и снова продолжение лучей крыш сойдется на базисе в точке М ₁. Ситуация повторится и для точек М ₂, М ₃ и т.д., и для точек N₁, N₂, N₃ и т.д. находящихся внутри пирамиды, и для точек, расположенных симметрично слева от пирамиды и от поляры. И можно полагать, что статичность бесконечных рядов гармонических точек находящихся на базисе, сохраняется при любом перемещении точки S над базисной прямой. Проверим, изменилась ли пропорциональность в расстояниях между крышами. Замерим эти расстояния. Они снизу вверх оказываются равными в см: 1,7; 2,6; 3,3; 2,6; 1,7. Т.е. высоты всех крыш наклоненной пирамиды, опирающейся на тот же базис, отличаются от высот пирамиды вертикальной. И плотность пространства по высоте пирамиды так же не остается неизменной. Она становится большей, поэтому расстояние между крышами уменьшается. Но и в этом случае уменьшение расстояний строго пропорционально и явно определена нейтральная зона одинаковой плотности в промежутке между третьей и четвертой крышей. Проверим по вурфному уравнению (4.2) сохранилась ли пропорциональность высоте между крышами?

W ₁ = 1,284; W ₂ = 1,283; W ₃ = 1,283; W ₄ = 1,284.

Т.е. вурфный коэффициент в пределах трех знаков не изменился, и пропорциональность расстояния между крышами сохранилась. Это очень важное обстоятельство, отображающее, например, природный процесс развития живых организмов. Известно, что части живых тел при росте изменяются на разную величину и, кажется, что это изменение происходит диспропорционально. Однако во всех случаях роста у всех растений и организмов, даже на клеточном уровне, сохраняется вурфная пропорциональность в изменении их жизненных органов, аналогичная пропорциональности элементов проективных пирамид.

Покажем, что те же ряды гармонических точек серий М и N можно построить, используя параллельные не Дезарга, а Евклида (рис. 60). У параллельных Евклида отсутствует точка опоры, и плотность пространства от базисной прямой постоянно уменьшается. Поэтому отсутствует по высоте нейтральная зона, а расстояние между крышами все время возрастает в геометрической прогрессии и приходится отыскивать ограниченное количество точек.

Проведем базисную прямую и отложим на ней отрезок АВ разделенный пополам точкой N. Из точек А, N, В восстановим перпендикуляры – параллельные. Параллельная прямая N становится полярой. Отложим на параллельных расстояние равное 0,5 АN, и соединим точки С и Д прямой. Образовавшийся прямоугольник АСДВ является прямоугольной трапецией, а прямая СД – его крыша. Через точку пересечение крыши СД с полярой проводим прямые – диагонали АД ₁ и ВС ₁, и соединив точки С ₁и Д ₁ получаем другую трапецию – квадрат АС ₁ Д₁В (двусмежный квадрат). Проведем диагонали в трапеции АС ₁ Д ₁ В и через их пересечение проведем прямую С ₂ Д ₂, параллельную базисной прямой. Получим еще одну трапецию АС ₂ Д ₂ В. Построение, как и в предыдущем случае, можно продолжать бесконечно как от базисной прямой, так и к ней.

Перейдем к нахождению гармонических точек. Проведем прямые через точки С ₃ Д ₂ и С ₂ Д ₁ до пересечения с базисной прямой. Они пересекут ее в точке М отстоящей от В ровно на длину АВ. Соединим точки С ₂ и Д, точки С ₁ и Д _о прямыми, продолженными до пересечения с базисной прямой. Они пересекут ее в точке М ₂. Таким образом можно найти и гармонические точки М ₃, М ₄ и т.д. Внутренние гармонические точки N ₁, N ₂, N ₃ит.д. также находятся на лучах, проложенных через точки пересечения прямых от крыш с полярой, до базисной прямой. \

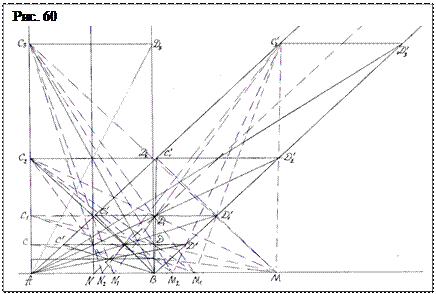Отметим одну особенность, характеризующую трапеции параллельных Евклида. Высоты их крыш возрастают точно так же, как возрастает базисный ряд русской матрицы, т.е. высоты их пропорциональны и структурированы по золотой пропорции 2,5; 5; 10; 20 и т.д., имеющей тот же вурф, что и расстояния между крышами аналогичной пирамиды Дезарга:

W _о = (2,5 + 5)(5 +10)⁄5(2,5 + 5 +10) = 1,286.

Теперь «наклоним» параллельные Евклида относительно базисной прямой на произвольный угол, и оставив высоту от базисной прямой до первой крыши равной АС´, соединим прямой точки С´ и Д´ (рис. 61). Через точку ее пересечения с полярой проведем диагонали АД ´ и ВС ´. Получим трапецию АС`Д ´ В. Через точку пересечения С´Д´ с полярой проведем диагонали и … т.д. Затем, аналогично предыдущему построению, проведем прямые С ₃´ Д ₂ ´ и С ₂ ´Д ₁´ и продолжим их до пересечения с базисной прямой в точке М ₁. Проведя С ₃´ Д ´ и С ´ Д ´ до пересечения с базисной прямой определим место точки М ₂. Аналогичным образом найдем точки М ₃, М ₄ и т.д. Внутренние точки N ₁, N₂, N₃ и т.д. находятся по лучам, проходящим от С ₃ ´, С ₂ ´, С ₁ ´ и т.д. через последующие центры поляр до пересечения с базисной прямой (рис. 61).

Таким образом, когда поляра проходит на равном расстоянии от двух параллельных, то построение гармоничных пропорций методом Дезарга и методом Евклида обусловливает нахождение одного и того же множества симметричных гармонических точек, как серии М, так и серии N. Если же расстояние от поляры до евклидовых параллельных различно, то крыши «едут». По мере удаления поляры от центра, наклон крыш увеличивается, а гармонические точки все больше приближаются к той прямой, к которой приближается поляра, и удаляются от другой параллельной (рис. 61). Пропорциональность и гармоничность же их не изменяется. Все операции нахождения серий точек повторяются аналогично предыдущему построению и точки оказываются в тех же местах, в которых они находятся у вертикальных параллельных.

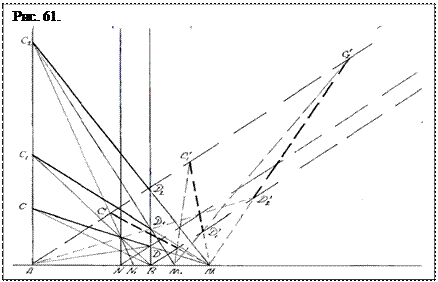Отметим также, что наклонение евклидовых параллельных, равноудаленных от поляры, не повлияло на положение крыш относительно горизонта. Они остались горизонтальными, и длина их не изменилась. Это следствия неизменной плотности пространства по горизонтали. Изменение плотности по вертикали приводит к тому, что параллельные боковины с удалением от базиса удлиняются следующим образом: 1,5; 2,9; 5,7; 11,4 и т.д. Но, тем не менее, пропорциональность их сохраняется, что и подтверждается вурфным коэффициентом: W₁ = 1,292; W₂ = 1,290.

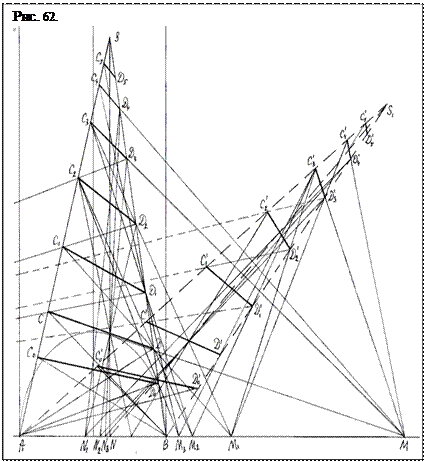
Коротко ознакомимся с характером изменения структуры проективной пирамиды при изменении положения поляры в круге. Отметим, что когда поляра проходит через центр окружности, т.е. когда пирамида симметрична, все ее крыши горизонтальны, а точки полюсов М и спутников поляры N на базисе расположены симметрично относительно нее. Каждая отдельная пара лучей крыш, вместе с базисной прямой, образовывают на бесконечности точки Дезарга симметрично по обе стороны пирамиды. Дискретное перемещение поляры вдоль диаметра сопровождается пропорциональным наклонением крыш с той стороны, в направлении которой она движется. А лучи от них, наклоняясь, «выходят» на базис одной, единой для всех точкой М и постепенно «проходят» все точки серии М. С противоположной стороны наклонение вызывает как бы «размыкание» точек Дезарга, поскольку, как свидетельствует рис.62, параллельность крыш нарушается. Но это нарушение параллельности – эффект картинки. Оно следствие изменения плотности пространства между параллельными сторонами пирамиды. И наклонение крыш не изменяет их параллельности, а только передвигает параллельные лучи к базисной прямой, имеющей бесконечную плотность, которая и «сводит» их в точку, перемещающуюся на базисной прямой вплоть до «соприкосновения» с окружностью в точке В.

С противоположной стороны пирамиды лучи от крыш движутся в пространстве уменьшающейся плотности, и потому возникает эффект их расширения. Постепенно наклон крыш приводит к тому, что виртуальные прямые, соединяющие точки С ₄, С ₃, С ₂ с точками Д ₃, Д ₂, Д _. оказываются параллельными базису, и по обе стороны пирамиды, возникают новые точки Дезарга. Дальнейшее перемещение поляры приводит к опусканию лучей виртуальных крыш на базисную прямую и возникновению нового полюса М. И чем дальше движется поляра, тем больше возникает новых полюсов, медленно перемещающихся вдоль базисной линии к основанию пирамиды. Однако все элементы деформируемой пирамиды, расстояния между полюсами и спутниками поляры сохраняют свою вурфную пропорциональность и гармонические отношения между отдельными четверками чисел. Проверим это утверждение на реальных цифрах, исходя из той же длины диаметра равной 10 см и высоты пирамиды равной 19 см.

4.3. Числа Фибоначчи и

золото статико-динамической геометрии

Предположим, в качестве примера, что в своем движении от центра круга к точке В поляра «случайно» заняла положение, соответствующее делению диаметра АВ золотым сечением, и пирамида стала асимметричной, как показано на рис.62 Часть структуры элементов фигур образуемая золотым сечением, как уже отмечалась выше, оказывается пропорциональной золотому числу. Поскольку основание пирамиды равно 10 см, то поляра разделяет его на две части длиной 6,1803 см больший отрезок и 3,8197 см - меньший. Поляра высотой 19 см пересекает семь этажей крыш, расстояния между которыми в см равны: 2,05; 2,8; 3,25; 2,95; 2,15; 1,3. Как и в симметричной пирамиде, расстояние между крышами остается неодинаковым, следствие анизотропности плотностного пространства пирамиды. Однако физическая пропорциональность между ними сохраняется, что и подтверждается коэффициентом вурфа, найденным по уравнению (4.2):

W ₁ = 1,286; W ₂ = 1,282; W ₃ = 1,284; W ₄ = 1,287.

Передвижение поляры из центра окружности вызвало наклонение крыш трапеций в сторону В, и лучи от них сходятся на точке М. В этой же точке базисную прямую пересекает касательная, исходящая от окружности в точке пересечения ее полярой. А это значит, что имеет место гармоническая четверка точек, определяемая равенством:

АN ⁄ВN = АМ ⁄ВМ

Решаем это равенство и получаем следующие величины образовавшихся отрезков: АМ = 26,18 см; ВМ = 16,18 см. Отрезок АМ по модулю равен десяти квадратам золотого числа Ф ² = 2,618, а отрезок ВМ по модулю равен десяти золотым числам Ф ¹ = 1,618. Числа эти существуют не сами по себе. Они члены числовой последовательности степенного греческого ряда, в котором каждый последующий член равен их сумме:

Ф ¹ + Ф ² = Ф ³ = 1,618 + 2,618 = 4,236. (4.4)

Здесь модуль величины Ф в степени определяет собой размерностную длину двух отрезков, а их сумма – длину всего отрезка.

Аналогично для модулей АМ и ВМ имеем:

1 а) ВМ + АМ = С ₁ Д ₁ = 16,18 + 26,18 = 42,36. (4.5)

Таким образом, пропорции четверки гармонических чисел проективной геометрии есть геометрическое отображение процесса нарастания (последовательного сложения) произвольных начальных величин чисел ряда Фибоначчи (метод сложения Фибоначчи).

Отметим, что такого типа суммирование в проективной геометрии не производится, хотя получение четырех точек достигается тем же способом, т.е. делением отрезка, отграниченного двумя точками, на два отрезка. Отношения получившихся отрезков и определяют гармоничность трех точек. В нашем случае это точки А, N, В.

Отрезки АN и ВN вместе и составляют отрезок АВ. Однако, повторимся, операция аналогичная сложению модулей отрезков АМ и ВМ как и отрезков АN и ВN в проективной геометрии не проводится. Проведем ее:

1 б) ВN + АN = АВ = 3,8197 + 6,1803 = 10,00. (4.6)

То, что величина АВ равна сумме ВN и АN, понятно и без записи равенства (4.6) поскольку именно АВ делилась в крайнем и среднем отношении. Но операция сложения полученных модулей отрезков, это не операция деления, а процесс выявления числовой структуры получаемых пропорций. Она-то и определяет факторы, обусловливающие гармоничность четырех точек, рассматриваемых в проективной геометрии, и бесконечного количества точек базисной прямой, которые появляются в статико-динамической геометрии. Именно поэлементное сложение (4.5) и (4.6) определяет структуру всех гармонических чисел и их взаимосвязь с золотыми пропорциями. И сумма отрезков как самостоятельная величина для данной фигуры, пропорциональная Ф ³, в (4.4), (4.5), (4.6) она, похоже, не употребляется в проективной геометрии.

Операции сложения:

АN + ВN = АВ,

АМ + ВМ = С ₁ Д ₁,

являются важнейшими операциями статико-динамической геометрии. Эти операции изначально предполагают потенцию непрерывного движения, поскольку производятся по правилу Фибоначчи, которое обусловливает бесконечное последовательное сложение двух чисел, при этом каждый последующий член ряда равен сумме двух предыдущих. Именно операция сложения модулей двух известных (АN и ВN) и двух неизвестных АМ и ВМ отрезков определяет начало ряда Фибоначчи и возможность гармонического пропорционирования четырех (многих) точек базисной прямой. Причем важнейшим обстоятельством пропорционирования является то, что в одно неизвестное число входит число известное, являющееся суммой двух известных чисел:

АМ = АВ + ВМ.

Этообстоятельство обусловливает пропорциональную на общий коэффициент взаимосвязь между известными и неизвестными длинами отрезков и, следовательно, возможность формализации одного уравнения с двумя неизвестными. В нем изначально закладывается пропорционирование как отношение неизвестных друг к другу через суммарное известное, входящее в неизвестное. Запишем это отношение:

АN ⁄ВN = (АВ +ВМ) ⁄ ВМ

И получаем уравнение из четырех членов с одним неизвестным ВМ. Преобразуя его, получаем:

ВМ = АВ·ВN ⁄ (АN – ВN). (4.7)

Следовательно, проекция поляры, в своем кадрированном движении вдоль диаметра, делит точками-полюсами базисную прямую на множество отрезков, гармонически пропорциональных его образовавшимся частям.

Если и в операциях (4.5) и (4.6) убрать знаки сложения и равенства, то перед нами два ряда начальных чисел Фибоначчи, сдвоенных в ряд Пилецкого. Сами по себе ряды Фибоначчи свидетельствуют об адекватности процессов, отображаемых ими отдельным природным зависимостям. Появление же ряда Пилецкого свидетельствует уже о наличии комплекса таких явлений, свидетельствует о развитии движения отдельных элементов во взаимосвязанную инвариантную систему, которая в дальнейшем вырождается в соответствующую матрицу. Модуль каждой тройки чисел (внутренних и внешних), двух слагаемых отрезков и результата, составляют ячейку из трех первых членов ряда А. Пилецкого. Двух рядов из трех чисел, каждый из которых в потенции последовательного сложения и умножения по вертикали на общий для них коэффициент в конечном итоге преобразуются в матрицу. В ряду Пилецкого числа одной строки отличаются от чисел другой на один и тот же коэффициент. Разделим каждое верхнее число на нижнее, и определим, связаны ли они единым коэффициентом:

16,18; 26,18; 42,36;

3,820; 6,180; 10,00;

коэффициент 4,236; 4,236; 4,236.

Коэффициент 4,236, единый для каждой пары чисел свидетельствует о том, что данный набор чисел есть сдвоенный ряд Пилецкого. Появление единого коэффициента пропорциональности между модулями параметров в пределах отрезка и с ним за его пределами в виде ряда Пилецкого обусловливает гармоничность множеству точек статико-динамической геометрии. Покажем развитие ряда Пилецкого посредством последовательного сложения чисел по горизонтали и умножения верхнего ряда на 4,24 и деления нижнего на те же 4,24 по вертикали (матрица 2).

Матрица 2

… … … … … …

… 42,37 68,53 110,9 179,4 290,3 …

… 10,00 16,18 26,18 42,36 68,54 …

… 2,360 3,820 6,180 10,0 16,18 …

… 0,557 0,902 1,459 2,361 3,820 …

… … … … … … …

В результате получаем, что сдвоенный ряд Пилецкого, образованный четверкой гармонических точек, является фрагментом одной из золотых русских матриц. Она изначально базируется на золотой пропорции и имеет следующие золотые коэффициенты взаимосвязи:

По строкам слева направо Ф ¹ – 1,618,

По диагонали слева направо сверху вниз Ф ² – 2,618.

По столбцам снизу вверх Ф ³ – 4,236,

По диагонали слева направо снизу вверх Ф ⁴ – 6,854,

Отметим одну существенную особенность фрагмента этой матрицы. Продолжим ряды Пилецкого за пределы фрагмента влево и вправо:

… 1,46; 2,36; 3,82; 6,18; 10,0; 16,18; 26,18; 42,36; 68,54; …

… …; …; …; 1,46; 2,36; 3,82; 6,180; 10,00; 16,18; …

И оказывается, что здесь наличествует последовательность чисел одного ряда, сдвинутого относительно друг друга на три числа. Эта операция сдвижения рядов, по-видимому, возникает потому, что поляра разделяет диаметр (или отрезок) в крайнем и среднем отношении. (Известно, что сдвиг числовых строк натурального ряда обусловливает и появление мифических квадратов.) Матрицы данного типа (русская матрица со сдвинутой строкой) образуют группу золотых многобазисных матриц и, похоже, наиболее адекватно отображают структуру окружающего космического пространства. В матрице базисная единица отображает плотностное пространство, которое в окружающем космическом пространстве представляют, например, планеты, звезды, галактики. Пропорциональность же чисел обеспечивает коэффициент пропорциональности – свой для каждого сдвоенного ряда. Выше показано, что всякое динамическое развитие проходит начальную стадию (последовательность) формирования рядов Фибоначчи с выходом на ряды Пилецкого и в дальнейшим с переходом в один из вариантов русской матрицы.

Покажем, что остальные точки серий М и N образуют подобные сдвоенные тройки чисел, которые могут формировать такие же фрагменты. По методу, описанному выше, находим несколько точек серий М и N и последовательно по уравнению (4.5)–(4.6) определяем расстояние их от точек А, В и N для проективной пирамиды рис. 62. Поскольку операция по нахождению расстояния до этих точек достаточно проста, проводить ее не будем, а, просто замерив и выписав полученные при построении расстояния до трех точек каждой серии в см, попробуем определить возможность взаимного пропорционирования их модулей: ВМ ₁ = 4,52; АМ ₁ = 14,52; ВN ₁ = 2,32; АN ₁ = 7,63; ВМ ₂ ==1,75; АМ ₂ = 11,75; ВN ₂ = 1,3; АN ₂ = 8,7; Это параметры точек расположенных по правую сторону от поляры (рис.62). Выпишем аналогичные параметры точек расположенных по левую сторону от поляры: АМ ´ = 42,32; ВМ ´ = 55; АN ´ = 4,5; ВN ´ = 5,5; АМ ´´ = 11,67; ВМ ´´ = 21,67; АN ´´ = 3,5; ВN ´´ = 6,5; АМ ´´´ = 6,91; ВМ ´´´ = 16,91; АN ´´´ = 2,9; ВN ´´´ = 7,1.

Отметим, что каждая из получаемых точек серий М отсекает на базисной прямой отрезок некоторой длины, пропорциональный определенным отрезкам, отсекаемым точками серии N на диаметре. Поэтому имеется возможность привести попарно сложение модулей величин этих отрезков, приводя их к виду (4.5)-(4.6).

Пары справа от поляры:

2 а) ВМ ₁ + АМ ₁ = С ₂ Д ₂ = 19,04; 2 б) ВN ₁ + АN ₁ = АВ = 10. (4.8)

3 а) ВМ ₂ + АМ ₂ = С₃ Д ₃ = 13,50; 3 б) ВN ₂ + АN ₂ = АВ = 10. (4.9)

Дата добавления: 2014-12-07