
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гармония золотых пропорций 3 страница
Возможность рассмотрения пропорционирования отдельно взятых элементов фигуры при их перемещении в плотностном поле опорной точки и базиса и послужила основой возникновения проективной геометрии, – геометрии, описывающей перемещение и деформации, вырезанных из фигур единичных элементов. В ней, как уже упоминалось ранее, рассматривается гармоническое отношение четверки точек, «выхваченных» из некоторой фигуры. Однако за гармоническим пропорционированием точек скрывается пропорционирование отрезков, которые находятся между этими точками. Сами же отрезки являются элементами скрытых фигур, которые «ускользнули» от рассмотрения на начальном этапе построения проективной геометрии и потому оказались не востребованными в ее основах. Познакомимся в общих чертах с обстоятельствами, обусловившими появление скрытых фигур и гармонизацию отношению четверки точек.
Начнем с параллельных, которые при их перспективном продолжении (т.е. в движении, которое никогда не кончается), на горизонте (на бесконечности) сходятся в точку, как бы пересекаются. Понятно, что точки пересечения нет, что это условность и параллельные остаются параллельными на бесконечности, но эффект как бы существует и Дезарг предложил считать точки мнимого «пересечения» параллельных в геометрии проекциями «бесконечно удаленных» точек. Более того, он также предложил считать бесконечно удаленные точки пересечения прямых – несобственные точки, равноправными всем остальным точкам. Таким образом, как говорится в [27]:«… Дезарг дополняет (!? Авт.) евклидово пространство новыми элементами: несобственными (бесконечно удаленными) точками, а также еще и плоскостью, на которой лежат все несобственные точки, – несобственной плоскостью. …И предлагает считать бесконечно удаленные точки равноправными (со всеми остальными) точками».
Прежде всего, Дезарг не дополняет евклидово пространство, поскольку таковое здесь не существует, а образует свое, вводя несобственное пространство и несобственные точки, и получая анизотропное плотностное пространство. Постулировав существование несобственной точки, Дезарг тем самым постулировал наличие в геометрии плотностного центра – основы аксиомы о динамических параллельных. Центр – точку, в которую входят параллельные как бы соединяясь в своем бесконечном движении. Точка «пересечения» параллельных на плоскости есть плотностная точка динамической геометрии. Точка, с приближением к которой пространство, окружающее ее, уплотняется, становясь проективным аналогом природного пространства, состоящего из физических точек различной плотности (эфира). Тем самым он, неявно, постулировал существование плотностного пространства и совершенно нового геометрического качества – плотностности, неизвестного в евклидовой геометрии. Принятое Дезаргом равноправие точек пересечения параллельных с точками евклидовой геометрии, не находящимися на бесконечности, аннулировало качество плотностности и формально превратило эти плотностные анизотропные точки, в изотропные точки евклидова пространства, которыми можно было оперировать по законам статической геометрии. Равноправие несобственных точек с евклидовыми точками скрыло их динамический характер.
Это «дополнение евклидова пространства» равнозначными несобственными точками инесобственным пространством требовало изменения представления о геометрическом пространстве, о точке, о взаимосвязях элементов фигур и о возможности движения в статической геометрии. Однако пересмотра не последовало. Постулирование несобственных точек и плоскостей обусловило появление новой статической проективной геометрии. В ней параллельные прямые отсутствуют. («У Дезарга две прямые одной плоскости всегда пересекаются. Ограничений никаких» [26]).
Повторимся – поскольку, по определению, параллельные прямые пересекаться не могут, то постулирование их пересечения вносит в неявной форме в евклидову геометрию противоречащее ей качество –кадрированное движение. Качество, которое свидетельствует о замедлении физического времени при движении к плотностному центру и полностью изменяет структуру статической геометрии, обусловливая возрастание «плотностности» пространства к области «пересечения параллельных прямых». В результате изотропное евклидово пространство автоматически, помимо нашего понимания и желания, становится пространством анизотропным, пространством, деформирующим тела, помещаемые в него при перемещении из одной области в другую. И это изменение качества евклидова пространства привело к появлениюгеометрическогодвижения и к деформации фигур и их элементов, не замеченных современниками:
Во-первых, потому, что в проективной геометрии рассматривалось перемещение не фигур, а точек, которые в движении не деформируются. Характерный пример – «гармоническая четверка точек». При перемещении их в пространстве проективной геометрии, отрезки между точками изменяются гармонически, а это изменение формулируется как отношение между точками.
Во-вторых, потому, что движение, по современным представлениям, происходит только в непрерывном времени, а время в статической геометрии отсутствует по определению.
В-третьих, не предполагалась даже возможность динамических изменений геометрических фигур.
В-четвертых, преобразование и деформация фигур в проективном пространстве было подменено так называемым сложным отношением четырех точек, за которым скрывалось отношение расстояний между точками, а не точек, и за этими точками существование геометрических фигур в пространстве даже не просматривалось. Понятие «сложное отношение четырех точек» тоже введено Дезаргом как простейшая величина, сохраняющаяся при проектировании, т.е. являющаяся инвариантом проективной геометрии.
Повторимся, – постулирование пересечения параллельных на бесконечности означает введение в статику элементов динамической геометрии. Для «достижения» точки «пересечения» параллельных на бесконечности им приходится двигаться в изменяемом плотностном пространстве. Т.е. перемещаться в ином пространственном качестве, внося в статическую геометрию элементы динамики. При этом параллельные динамической геометрии не пересекаются, а «входят» в плотностную точку динамической геометрии и никуда из нее не выходят. Именно плотностная точка и является физическим аналогом несобственной точки Дезарга. К тому же существование несобственной точки не является фактом пересечения параллельных, а только свидетельством некоего сближения линий на горизонте в процессе бесконечного движения вглубь плотности, воспринимаемого как плотностная точка. И поэтому несобственные точки никогда не могут быть равноправными и равнозначными с геометрическими точками, поскольку несобственные точки существуют как отображение в геометрии плотностной телесности пространства. Несобственные точки – порождение динамической аксиомы о параллельных. Они суть свидетельства бесконечного кадрированного геометрического движения фигур в плотностном поле, которое и есть время. С их введением в геометрию последняя качественно изменяется. Статическая геометрия Евклида приобретает динамику, а вместе с ней и новое проективное пространство, – плотностное анизотропное пространство, в котором фигуры и их элементы, перемещаясь, деформируются, т.е. взаимодействуют с пространством.
С появлением несобственных точек и плоскостей, обусловивших возможностью перемещения базисных фигур, в геометрии появилась и возможность перемещения отдельных элементов; точек, отрезков, фигур, причем таким образом, что наличие фигур, в которые эти элементы входили, становилось незаметным, скрытым. И существование таких скрытых фигур сохраняется на протяжении всего существования проективных геометрий. Рассмотрим, как это произошло, какие фигуры оказались скрытыми, и какие последствия обусловило существование несобственных точек в геометрии.
4.2. Скрытые фигуры
статико-динамической геометрии
Остановимся на процессе появления четырех точек на прямой. В предыдущей главе коротко описан этот процесс и показано наличие окружности, поляры ТТ `` с отметкой N на диаметре АВ и полюса М на продолжении диаметра (рис. 54). Вместе с точками А и В, лежащими на пересечении прямой окружностью, получается только две пары точек: одна на окружности А и В, а вторая – полюс М и точка N пересечения диаметра с полярой ТТ´. Рассмотрение и ограничивается четырьмя точками на прямой А, N, В, М. Отметим еще раз главное: отношение длин отрезков АN и NВ равно отношению длин отрезков АМ и ВМ.
А N⁄NВ = АМ⁄ВМ (4.1)
Точки этого отношения, N и М, разделяют отрезок АВ гармонически и совместно называются гармонической четверкой точек. Особо отметим, чтоцентр окружности, построенной на диаметре АВ, не входит в структуру проективной геометрии и не 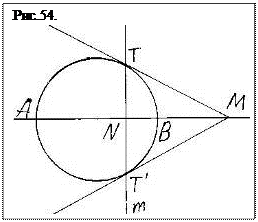 является не только гармонической, но и значимым элементом проективной фигуры. И все перемещаемые отрезки с четырьмя гармоническими числами, не включают в себя центр окружности как некое расстояние, гармоничное остальным ее отрезкам. Неизменным остается количество точек на прямой и ее единственный полюс − М. Подчеркнем еще раз – в проективной геометрии на прямой существует единственный полюс М. И этот полюс не имеет отношения к фигуре. Ни сама фигура, ни ее элементы не распространяются на другие направления пространства, что обедняет и делает односторонней всю структуру проективной геометрии. И потому сама фигура (рис. 54) остается «однобокой» и асимметричной.
является не только гармонической, но и значимым элементом проективной фигуры. И все перемещаемые отрезки с четырьмя гармоническими числами, не включают в себя центр окружности как некое расстояние, гармоничное остальным ее отрезкам. Неизменным остается количество точек на прямой и ее единственный полюс − М. Подчеркнем еще раз – в проективной геометрии на прямой существует единственный полюс М. И этот полюс не имеет отношения к фигуре. Ни сама фигура, ни ее элементы не распространяются на другие направления пространства, что обедняет и делает односторонней всю структуру проективной геометрии. И потому сама фигура (рис. 54) остается «однобокой» и асимметричной.
На рис. 55 эти элементы, обусловливающие образование четырех гармонических точек, доведены до симметричного вида и показаны в своей полноте. На нем показано, что гармонических точек оказывается не четыре, а, по меньшей мере, пять. Добавилась точка М 1. В центре круга под прямым углом пересекаются базисная прямая на которой расположен диаметр АВ, и поляра ТТ´. Через точки А и В проходят евклидовы параллельные прямые (на рис. 55 изображены штрихами). Прямые АS и SВ, как и АS 1 и S 1 В есть параллельные Дезарга. Они «пересекаются» на бесконечности в точках S и S 1 на поляре, и потому эти точки являются несобственными плотностными точками. Образуемые фигуры, подобные треугольники АSВ и АS 1 В, симметричны относительно базисной прямой (рис. 55). Они могут быть названы проективными пирамидами.
Поляра ТТ´ – геометрическое отображение на плоскости зоны одинаковой плотностности между параллельными. Физически же поляра есть область пространства, в которой плотностные параметры двух параллельных совпадают. Это своего рада нейтральная зона между ними. Она существует, пока существуют «плотностные» параллельные. Смещение поляры как нейтральной зоны к одной из параллельных означает, что другая параллельная имеет большую плотностность. Точка S хорошо известна в проективной геометрии, но известна как центр проекции, а не как неотъемлемый элемент поляры ТТ`. Она – несобственная точка на поляре полюсов М и М 1, названная выше точкой опоры. Точка опоры S – базисная точка, точка, не имеющая центра, плотностное пространство статико-динамической геометрии, в которую со всех сторон сходятся параллельные лучи.
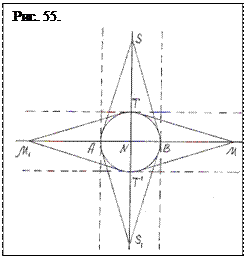 Через точки пересечения поляры ТТ´ с окружностью на бесконечность проведены касательные (показано штрихами). На бесконечности данные касательные тоже «пересекаются» на базисной прямой и точки их пересечения становится несобственными точками, – полюсами серии М. Их расположение тоже симметрично. Т.е. на бесконечности полюс М изменяет свое качество и в этом случае оказывается не просто точкой, а несобственной точкой Дезарга. И бесконечная, на которой расположен отрезок АВ и точка М, становится своего рода многоточечной, неподвижной полярой. Это очень важное обстоятельство, не отмеченное в проективной геометрии, меняет представление как о четырех гармонических точках, так и о структуре проективной геометрии.
Через точки пересечения поляры ТТ´ с окружностью на бесконечность проведены касательные (показано штрихами). На бесконечности данные касательные тоже «пересекаются» на базисной прямой и точки их пересечения становится несобственными точками, – полюсами серии М. Их расположение тоже симметрично. Т.е. на бесконечности полюс М изменяет свое качество и в этом случае оказывается не просто точкой, а несобственной точкой Дезарга. И бесконечная, на которой расположен отрезок АВ и точка М, становится своего рода многоточечной, неподвижной полярой. Это очень важное обстоятельство, не отмеченное в проективной геометрии, меняет представление как о четырех гармонических точках, так и о структуре проективной геометрии.
Перемещение полюса М из бесконечности в зону окружности не отражается на его новом качестве, оставляя ему значимость несобственной плотностной точки. Следовательно, и геометрия пространства, заключенного в промежутке ТМТ` должна некоторым образом отличаться от пространства евклидовой геометрии, поскольку вблизи окружности и в ней появились точки разного несовместимого качества. В целом крестообразная фигура, может быть названа проективным крестом, и имеет способность кадрировано изменяться (деформировать), так как точки опоры S и S 1 могут перемещаться в любую область пространства над базисной прямой, вызывая деформацию всей фигуры, заключенной в структуру пирамиды (кроме основания). Поскольку двойки параллельных прямых, касательных к окружности, пересекаются под углом 90о и проходят за ее пределы на бесконечность вверх и вниз, вправо и влево, то согласно Дезаргу, во всех четырех направлениях они на бесконечности пересекаются в несобственных точках М, М 1, S, S 1 и др., лежащих на базисной прямой и поляре, а образуемая ими в скрытой форме первичная фигура есть проективный крест (рис. 55.).
Таким образом, фигура проективного креста представляет собой геометрическое единое. Все элементы ее взаимосвязаны и взаимообусловлены. Причем точки опоры серии S хотя и принадлежат фигуре и входят в целое, являются достаточно «самостоятельными» объектами и как бы «отделены» от окружности своей нейтральной зоной, проходящей внутри пирамид. То, что точка S способна «перемещаться» в любую область пространства, а не только по поляре, свидетельствует о том, что в любой области пространства существуют аналогичные плотностные точки, являющиеся невидимыми элементами пространства. И каждый элемент фигуры: точки, отрезки, пирамиды и т.д., являясь отдельным, обладает возможностью «самостоятельного движения», которое все равно будет происходить по законам движения единого. В современной проективной геометрии фигура как единое не рассматривается.
Фигуру, несколько напоминающую проективный крест – окружность, с тремя вертикальными касательными, только повернутую на 90о, мы уже встречали при рассмотрении процесса деления отрезка в крайнем и среднем отношении. Это три параллельные на рис. 50, пересекающие бесконечную прямую АВ в точках А, В и N, только там прямая ТТ` проходила не через центр окружности. Эти параллельные перенесены на рис. 55 и отмечено, что точка N в этом случае оказывается проекцией прямой ТТ´ на диаметр, а сама прямая – полярой, которая может перемещаться по диаметру от точки В к центру окружности вызывая перемещение полюса М, образуемого касательными, от точки В вправо от окружности. То же самое происходит при перемещении поляры от точки А с левой стороны фигуры вправо, где аналогом точки М становится точка М 1. Перемещение поляры в промежутке между точками А и В вызывает асимметрию пирамид и сопровождается пропорциональным перемещением касательных к окружности ТТ ´, а вместе с ними и образуемых ими полюсов. При перемещении к окружности полюса серии М остаются несобственными точками еще и потому, что они перемещаются по несобственной базисной прямой.
Еще раз остановимся на элементах, образующих проективный крест на плоскости. Основу его составляет окружность, пересекаемая бесконечной базисной прямой на которой отрезок АВ является диаметром. Базисная прямая (базис) – геометрический абсолют всей плоскости, на которой располагаются (можно сказать «закрепляются») связанные с ней фигуры. К тому же сама она может являться плотностной линией на горизонтальной плоскости. Она и опорная точка – элементы, могущие поочередно становиться то статическими, то динамическими в статико-динамическом плотностном пространстве. Однако всегда в этом пространстве находится фигура, играющая роль базиса. Без базиса в виде опорной точки, прямой или плоскости плотностное пространство проективной геометрии отсутствует. Базисная прямая, как будет показано далее, содержит бесконечное количество несобственных гармонических точек серии М (а не четыре, как принято в современной проективной геометрии). Гармонические точки – проекции отдельных элементов фигуры заключенной в пирамиду АSВ на базисную прямую. Проекции, которые сами могут представлять собой динамические параллельные, проектирующиеся в точку на базисной прямой. Положение каждой из точек обусловлено продолжением луча от определенного элемента или элементов фигуры до пересечения с базисной прямой. Все эти точки включены в пространство, образуемое точкой опоры и базисной прямой. Перемещение фигуры на плотностной плоскости, как и в аналогичном физическом пространстве, деформирует ее, но не меняет места нахождения гармонических точек, отображающих эти элементы на базисе.
Пространство внутри окружности, похоже,является базисом фигур. Базис фигуры включает точки А, В, N и образует (охватывает) фигуру вместе с опорной точкой S, лучи от которой проходят как через элементы фигуры, так и через гармонические точки. Точка опоры S со сходящимися в нее лучами (пучки лучей) является динамической частью фигуры. Она может перемещаться в любую область пространства, в то время как ее основание и поляра не покидает своего места на базисной прямой. Гармонические точки и полюса могут передвигаться, следуя за лучами, исходящими от элементов пирамиды к базисной прямой.
Характер деформации всей фигуры определяется той областью пространства, в которую перемещается точка опоры S. Она – отображение возможности бесконечной деформации фигуры. Точка опоры может приобретать статус статического параметра (неподвижного базиса) в том случае, когда базисная прямая переносится в другую область пространства, как перед точкой опоры, так и на продолжениях лучей за ней, т.е. базис приобретает возможность передвижения, теряя статус неподвижного. В этом случае именно точка опоры приобретает этот статус и «сохраняет» структуру фигуры включенной в базис. Расстояние же между гармоническими точками на базисе, при его перемещении, изменяются без нарушения их гармонии. Базисная линия, как уже упоминалось, может иметь любую конфигурацию, в том числе в виде окружности или эллипса. Точки опоры, и не в единственном числе, могут находиться внутри или снаружи этих эллиптических фигур
Почти все перечисленные выше фигуры и связанные с ними понятия в современной проективной геометрии отсутствуют. И их отсутствие не случайно. Оно следствие следующей операции, проведенной, по-видимому, тем же Дезаргом. Процитируем ее из того же источника [27]:
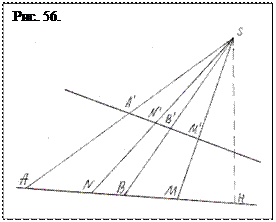
«Уберем с нашего чертежа (рис. 54) окружность и поляру, оставим только их «следы» – саму прямую, точки А и В, полюс М и точку N, т.е. оставим четверку точек на прямой. Вне этой прямой возьмем точку (S), которую будем считать центром проекции, а лучи, проходящие через центр и гармоническую четверку точек, будем называть гармонической четверкой лучей. Замечательно (!!!–Авт.) что на любой другой прямой, пересекающей эти лучи, четверка новых точек – А, В, М, и N` − (рис.56.) снова будет гармонической».
Это небольшое описание содержит несколько допущений естественных для времени Дезарга и оставшихся в проективной геометрии до настоящего времени.
Первое и важнейшее – без всякого обоснования с чертежа убираются взаимосвязанные элементы, являющиеся основной частью единого, обусловливающие возможность объяснения взаимосвязи гармонической четверки точек. Эта операция и закрепила статический характер проективной геометрии и все ее дальнейшее однонаправленное развитие.
Второе заключается в том, что опорная точка S, как и точка М, считаются простыми точками, независимыми от базиса. Не отмечено также, что S и М – несобственные точки.
Третье – базис рисунка прямая АМ, перемещаемый в другую область пространства, как и новое его положение А`М`, постулируются случайными линиями, не обладающими свойствами базисной прямой.
Четвертое – не объяснено, почему на «любой прямой», пересекающей лучи, сохраняется гармоничность четырех новых точек. Более того, по описанию фигур это сохранение оказывается случайным «замечательным» свойством и потому, по-видимому, не требующим объяснения.
 И, наконец, последнее – не замечено, что представленная на рис. 54 фигура не полна. У нее отсутствует несколько элементов, обнаруженных в структуре золотого сечения и отображенных на рис. 55, а точки М, как след касательной, и S, как опорная точка, остаются плотностными точками и, потому, не могут появляться случайно.
И, наконец, последнее – не замечено, что представленная на рис. 54 фигура не полна. У нее отсутствует несколько элементов, обнаруженных в структуре золотого сечения и отображенных на рис. 55, а точки М, как след касательной, и S, как опорная точка, остаются плотностными точками и, потому, не могут появляться случайно.
Само перемещение базиса из одной области в другую, сопровождаемое изменением (деформацией) расстояния между четырьмя точками, отображает только два момента (кадра) их размещения. Причем начальный кадр движения базиса проходит бесчисленное количество «рывков» и «остановов», не отмечаемых на рисунке, прежде чем зафиксируется на новом месте и в новых пропорциях. Поскольку отношение отношений между точками не всегда равнялось единице, то оно получило название сложного отношения четырех точек.
Но сейчас вернемся к фигуре на рис. 54 и попробуем восстановить все ее элементы, включая не проявленные – т.е. те, которые получены при рассмотрении золотого сечения. Попробуем качественно, не прибегая, к аксиомам, теоремам и алгебраическим доказательствам, показать пропорционирование фигур и их элементов с использованием линейки и циркуля (пропорционирование линейкой и циркулем достаточно для качественного рассмотрения предмета исследования).
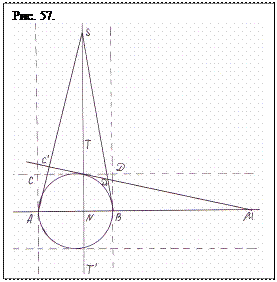 Начнем с базисной линии, проходящей на бесконечность через точки образующие отрезок АВ (рис. 57). Разделим отрезок АВ пополам и из точки О, как из центра, опишем радиусом АО окружность. Методом двойного квадрата найдем точку N и восстановим перпендикуляр к базису, – прямую, пересекающую окружность в точках ТТ` и являющуюся полярой для точек лежащих на базисе, а через точки А и В проведем касательные к окружности и прямые, сходящиеся на поляре. Получаем три бесконечные параллельные прямые евклидовой геометрии (штрихованные лини), или две параллельные Дезарга пересекающиеся на поляре – прямой ТТ` в точке S, причем поляра становится основой образовавшейся треугольной проективной пирамидой АSВ. Через верхнюю и нижнюю части окружности проведем касательные параллельные базисной прямой и получим три, аналогичные вертикальным, горизонтальные параллельные Евклида (штрихованные линии). Построение закончено. И вместе с пирамидой Дезарга получен двусмежный квадрат АСДВ фигура, представляющая собой прямоугольную трапецию, опирающуюся на параллельные Евклида и разностороннюю трапецию АС`Д`В, опирающуюся на параллельные Дезарга. Симметричные элементы фигуры могут быть получены, как показано на рис 55, и в точках М 1 и S 1 на противоположных сторонах проективного креста, но их рассматривать не будем.
Начнем с базисной линии, проходящей на бесконечность через точки образующие отрезок АВ (рис. 57). Разделим отрезок АВ пополам и из точки О, как из центра, опишем радиусом АО окружность. Методом двойного квадрата найдем точку N и восстановим перпендикуляр к базису, – прямую, пересекающую окружность в точках ТТ` и являющуюся полярой для точек лежащих на базисе, а через точки А и В проведем касательные к окружности и прямые, сходящиеся на поляре. Получаем три бесконечные параллельные прямые евклидовой геометрии (штрихованные лини), или две параллельные Дезарга пересекающиеся на поляре – прямой ТТ` в точке S, причем поляра становится основой образовавшейся треугольной проективной пирамидой АSВ. Через верхнюю и нижнюю части окружности проведем касательные параллельные базисной прямой и получим три, аналогичные вертикальным, горизонтальные параллельные Евклида (штрихованные линии). Построение закончено. И вместе с пирамидой Дезарга получен двусмежный квадрат АСДВ фигура, представляющая собой прямоугольную трапецию, опирающуюся на параллельные Евклида и разностороннюю трапецию АС`Д`В, опирающуюся на параллельные Дезарга. Симметричные элементы фигуры могут быть получены, как показано на рис 55, и в точках М 1 и S 1 на противоположных сторонах проективного креста, но их рассматривать не будем.
Отметим, что только два элемента фигуры, изображенной на рис. 57 могут перемещаться при фиксированном положении диаметра на базисной прямой: это точка опоры S и поляра ТТ´ причем само перемещение поляры свидетельствует об изменении плотности пространства между параллельными. Точка опоры S, как уже говорилось, может перемещаться в любое место пространства над базисной прямой вне окружности и внутри нее. Потенциальная возможность нахождения S в любой области пространства и обусловливает образование статико-динамического плотностного пространства. Ее перемещение по высоте или в стороны вызывают изменение величины угла S пирамидального треугольника АSВ и пропорциональную деформацию всех элементов, которые могут находиться внутри пирамиды. Перемещение в стороны вызывает наклон пирамиды и параллельных Евклида, проходящих через точки А и В. Точки же серии М лежащие на базисе и являющиеся проекциями определенных элементов пирамидальной фигуры АSВ перемещаться не могут. Они статичны пока пропорция АN∕NВ неизменна. Расстояние между ними пропорционально изменяется только тогда, когда перемещается сама базисная прямая (как, например, на рис. 56).
Поляра ТТ` (рис. 55), обуславливая структуру всей получившейся фигуры, может перемещаться двигаясь внутри окружности параллельно самой себе либо к точке А, либо к точке В, превращая при этом фигуру пирамиды из симметричной относительно поляры проходящей через центр, в асимметричную. Причем это движение будет сопровождаться не только перемещением точек полюсов серии М вдоль базиса и их исчезновением, но и проявлением новых гармонических точек-полюсов, как проекций других элементов фигуры на базис: М 1, М 2, М 3, … и т.д. (Как следует из рис. 54 несобственные точки серии М появляются и при пересечения касательных к точкам Т или Т` с базисной прямой.) Точки серии М на базисной прямой есть плотностные геометрические образования в плоскости базиса, в которые входят лучи-прямые от отдельных элементов фигуры. Они имеют различную плотностность на различном расстоянии от точек опоры или от элементов фигур, от которых исходят лучи. Перемещение точки опоры S в пространстве над базисом вызывает либо изменение пирамиды по высоте, либо ее наклонение, но не изменяет ни пропорций точек на базисе, ни вурфных отношений элементов наклоняемой фигуры. Местонахождения ни одной точки М на базисе мы, по пирамиде без структурных элементов, определить не можем. Поэтому, перейдем сначала к рассмотрению способов нахождения четвертой гармонической точки – полюса без опоры на касательную к точке пересечения окружности полярой.
Вернемся к рис. 54 и отметим, что еще Дезарг определил способ нахождения четвертой гармонической точки по трем данным без использования касательной. Приведем из работы [27] описание этого способа: «Дезарг провел следующее построение (рис. 58), в котором точки и прямые занумерованы в порядке их появления: точки 1, 2, 3 на прямой р даны сразу, через точку 1 проводятся две произвольные прямые 4 и 5, затем через точку 2 – произвольная прямая 6, затем находятся точки 7 и 8 ее пересечения с прямыми 4 и 5, через каждую из этих точек и точку 3 проводятся прямые 9 и 10, получается точки 11 и 12, через них проводится прямая 13, которая и пересекает исходную прямую р в точке 14. Дезарг доказал, что эта точка является искомой четвертой гармонической к точкам 1, 2, 3».
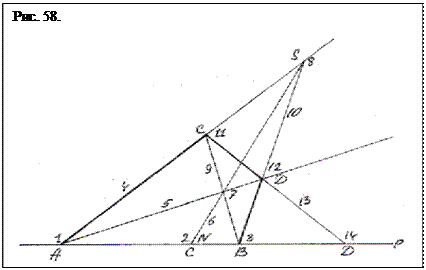 Отметим, что в построении фигуры (рис. 58) не использовались ни окружность, ни касательная и даже не упоминается поляра 6, хотя понятно, что она всегда находится между А и В. И тем не менее четвертая гармоническая точка найдена. Рассмотрим фигуру, полученную Дезаргом «произвольным» проведением двух прямых и вовсе не случайно копирующую выстроенную выше (рис. 57) вертикальную проективную пирамиду. Чтобы убедиться в этом, поменяем нумерацию Дезарга на использованную выше индексацию (рис. 57). Итак, на фигуре рис. 58 изображена наклонная проективная пирамида 183 (АSВ) с точкой опоры S, образованная параллельными Дезарга, и опирающаяся на отрезок 1, 3 (АВ) базисной прямой. Прямая, соединяющая точки 8 (S) и 2 (N) – наклоненная поляра (SN –рис. 57), проходящая правее центра окружности. Линия p, на которой расположены четыре гармонические точки – базисная прямая.
Отметим, что в построении фигуры (рис. 58) не использовались ни окружность, ни касательная и даже не упоминается поляра 6, хотя понятно, что она всегда находится между А и В. И тем не менее четвертая гармоническая точка найдена. Рассмотрим фигуру, полученную Дезаргом «произвольным» проведением двух прямых и вовсе не случайно копирующую выстроенную выше (рис. 57) вертикальную проективную пирамиду. Чтобы убедиться в этом, поменяем нумерацию Дезарга на использованную выше индексацию (рис. 57). Итак, на фигуре рис. 58 изображена наклонная проективная пирамида 183 (АSВ) с точкой опоры S, образованная параллельными Дезарга, и опирающаяся на отрезок 1, 3 (АВ) базисной прямой. Прямая, соединяющая точки 8 (S) и 2 (N) – наклоненная поляра (SN –рис. 57), проходящая правее центра окружности. Линия p, на которой расположены четыре гармонические точки – базисная прямая.
Все основные элементы совпадают. Но у Дезарга имеются еще три прямые, которые отсутствуют на рис. 57. Это 5, 9, и 13. именно пересечение последней базисной прямой и определяют местоположение четвертой гармонической точки Д (М). В структуре наклонной пирамиды эти прямые образуют разностороннюю трапецию А11,12,В, у которой прямые 5 и 9 пересекаясь на поляре 2, оказываются диагоналями данной трапеции. Появление в структуре пирамиды, не отмеченной трапеции, свидетельствует об отсутствии в проективной геометрии этой фигуры, отметим – принципиально важного элемента для понимания динамической сути всей проективной геометрии. Если же пирамиду «выпрямить», а это равнозначно перемещению поляры в центр окружности (рис. 55.), то верхнее основание трапеции «повернется» и станет параллельно нижнему основанию. Если же поляру отодвинуть от центра, то верхнее основание наклонится (рис.58) А сама трапеция окажется полным аналогом трапеции АС`Д`В (рис. 57). Если же теперь в трапеции АС´Д´В провести диагонали, то они пересекутся на поляре и данная трапеция окажется аналогом трапеции А11,12,В.
Таким образом «случайно» проведенная прямая 5 становится не случайным элементом трапеции – одной из ее диагоналей, а прямая 9, соединяющая точку В и точку 11 – другой диагональю. Следовательно, точки поляры являются местом пересечения прямых – диагоналей, исходящих из А и В. Прямая же, соединяющая их пересечение с вертикальными параллельными Дезарга, верхнее основание трапеции, становится как бы «крышей», «надвинутой» на диагонали, и завершающей построение одной трапеции. Но через поляру может проходить множество диагоналей, и потому в пирамиде потенциально «запрятано» неограниченное число трапеций. Рассмотрим, что же дает построение нескольких пропорционированных трапеций в симметричной пирамиде (рис. 59).
|
|
Дата добавления: 2014-12-07; Просмотров: 485; Нарушение авторских прав?; Мы поможем в написании вашей работы!