Гармония золотых пропорций 2 страница

Теперь, имея некоторое представление о древних саженях, попробуем определить, какие же размеры имеет храм, построенный Соломоном для Господа. Сначала определимся, какой информацией мы располагаем, кроме знания о назначении саженей:

Прежде всего, нам неизвестны сакральные числа религии времен Соломона, хотя два из них – 3 и 10 заложены в параметрах 20, 30, 60. Нам известно, что еврейский народ, незадолго до построения храма, в течение сотен лет проживал в земле египетской и, значит, пользовался теми же строительными инструментами, что и египтяне. Следовательно, можно предположить, что два других египетских сакральных числа 7 и 11 могут входить в структуру храма, и сделать вывод о том, что зодчие Соломона работали по египетскому канону. На это указывает и длительность строительства храма. Ясно также, что при проектировании храма использовались бóльшие строительные локти (например, полуторные), чем в доме Соломона. Наконец один из параметров должен давать единственное решение, т.е. иметь одно сакральное число. Скорее всего, это ширина в 20 локтей. Теперь можно приступать к нахождению метрических величин параметров храма Господа именно с его ширины.

Запишем метрические размеры локтей и, умножив их на 20, определим возможные параметры ширины храма Господа. Эти размеры последовательно поделим на числа кратные 7 и 11. В результате получаем размер, в котором укладываются все египетские и христианские сакральные числа. Расчет показывает, что ширина храма равнялась примерно 21,3 метра, и в ней укладывалось полуторных локтей городовых 20; 1,068 х 20 = 21,36 м, полуторных локтей больших 22; 0,969 х 22 = 21,32 м и локтей меньших 42; 0 ,5045 х 42 = 21,19 м. И, получаем, что параметры храма включали все сакральные числа: 1(0), 7 (7х3х2), 11 (11х2). Зная это, находим высоту и длину храма. Они оказываются равными следующим величинам: высота равна 25,90 м и в ней укладываются 33 полуторных локтя фараона; 0,7842 х 33 = 25,88 м, 35 локтей царских; 0,74 х 35 = 25,90 м, и 30 полуторных локтей греческих; 0,864 х 30 = 25,92 м. Длина равна 39,56 м и в ней укладываются полуторных локтей народных 60; 0,66 х 60 = 39,6 м, кладочных 66 локтей; 0,599 х 66 = 39,53 м и простых 70 локтей; 0,5655 х 70 = 39,58 м. Главные размеры храма Господа, построенного Соломоном, определены. Каждый его параметр размерялся тремя различными полуторными саженями, т.е. храм обладал высшей степенью святости.

Теперь, для сопоставления, тем же методом, рассчитаем размеры, которые имел дом Соломона, исходя из того, что его параметры размечались одинарными локтями. За точку отсчета снова берем количество локтей, включающее одно сакральное число – 50. И находим, что дом Соломона имел следующие размеры: высоту – 15,42 м, в которой укладывались 33 локтя церковных и 35 локтей народных, ширину – 18,9 м, в которой укладывалось 33 локтя греческих, 50 локтей простых 56 локтей меньших и длину 39,9 м, где укладывалось локтей Пилецкого 77, и кладочных 100. И дом самого Соломона по объему оказывается меньше храма Господа почти в два раза, да и времени на его сооружение Соломон затратил больше, чем на сооружение храма Господня.

Похоже, что можно не ограничиваться получением главных размеров храма Господня, но и выявить величину и структуру тех элементов, из которых он складывается. Полное описание храма дается пророком Иезекиилем. Используя это описание и методы проективной геометрии, учитывая, что три основных размера храма есть сложное отношение трех исходных точек, можно, по описанию, определить все элементы храма. Но это отдельная и большая задача, решение которой не является целью данной работы. Поэтому вернемся к теме и продолжим рассмотрение качественных особенностей статической геометрии.

3.5. Фигуры золотого сечения

Задачу деления отрезка в крайнем и среднем отношении (Рис. 42) можно описать двумя размерностными уравнениями:

(a + c)/c = c/a (3,31)

(a + c)/a = (c/a) ², (3.32)

И решать тремя способами:

● алгебраическим, подставляя в (3.31) или (3.32) b = с ⁄ а и получая алгебраическое уравнение:

b ² – b – 1 = 0, (3,33)

не имеющего отношения ни к (3.31) ни к (3.32) поскольку в (3.33) отсутствует размерность, и к тому же решение ограничивается только нахождением безразмерностного числа Ф.

● геометрически, с помощью линейки и циркуля, или приведением уравнений (3.31) и (3.32) к геометрической форме посредством освобождения от знаменателя:

a ² + ac = c ², (3,34)

и после замены ас на b ² имеем уравнение Пифагора для прямоугольного треугольника,

a ² + b ² = c ², (3,35)

где b длина одного из катетов треугольника имеющая размерность. Появление b свидетельствует о том, что первичный отрезок АВ, по-видимому, является отображением в виде прямой некоторой фигуры, находящейся на горизонтальной плоскости, а точки А, В, С, значимые точки этой фигуры.

● и, как показано выше, совместным решением (3.31) и (3.35) – находя величины всех параметров, задействованных в уравнении (3.31).

Но появлением (3.31)-(3.35) количество возможных формализаций результатов деления отрезка в крайнем и среднем отношении не ограничивается. Не исключено, что этой операцией не отрезок делится надвое, а находится отношение длин некоторых параллельных отрезков АВ, АС, и ВС (рис. 49.1) расположенных на соответствующем расстоянии друг от друга торцом к наблюдателю и для них можно записать следующую пропорцию:

АВ ∕ АС = АС ∕ ВС. (3,36)

И это не все. Уравнение (3.35) может оказаться не уравнением Пифагора, а формализацией положения окружности на плоскости, достаточно преобразовать его в следующий вид:

а ² ∕ с ² + b ² ∕ с ² = 1. (3,37)

Вот тот набор фигур, которые могут «скрываться» на плоскости за формулировкой «деление отрезка в крайнем и среднем отношении». И у нас отсутствует основание для игнорирования анализа любого из этих уравнений. Начнем рассмотрение с уравнения (3.35), поскольку именно в нем проявляет себя появление третьего отрезка.

Как следует из (3.35) в результате деления отрезка АС на две части получены три отрезка образующие прямоугольный треугольник, что логически невозможно. К тому же остается неясным механизм выявления размерностного Ф, и отсутствуют ответы на вопросы: Откуда появляется третий отрезок в уравнении Пифагора (3.35), ведь согласно уравнению (3.31), отрезок делится на две, а не на три части? Действительно ли уравнения (3.31), (3.32) воспроизводят деление отрезка, или совместно они отображают какие-то другие геометрические фигуры? Если фигуры, то какие? Можно ли по одной доле отрезка, а или с, решить обратную задачу: восстановить его полную длину геометрическими методами (с помощью линейки и циркуля)? Попробуем разобраться в этих вопросах.

Сначала отметим, что предполагаемая прямая может оказаться горизонтально расположенной плоскостью с нанесенными на ней одной или несколькими фигурами, которые в таком случае будут невидимы, или проявят себя в виде отрезка. И потому процесс «деления» оказывается не только делением, но и выявлением на «ребре» плоскости элементов какой-то фигуры или фигур, расположенных в промежутке между точками А и С. Вероятно поэтому для деления отрезка АС с помощью циркуля и линейки приходится строить, как это показано ранее на рис. 47, вспомогательный двусмежный квадрат АСДВ.

На рис. 47. точка N, делящая отрезок в золотой пропорции, найдена. Она становится значимой, поскольку вместе с А и В может отображать, например, существование трех евклидовых параллельных прямых, видимых с торца. Данное отображение не проявляет наличия параметра b, но и не отрицает возможность существования евклидовых параллельных. Такой вариант не исключается, поскольку три искомые точки А, В, и N наличествуют, и его нельзя отбросить без рассмотрения. Другой вариант – возможность наличия двусмежного квадрата на плоскости, используемого для геометрического деления отрезка в крайнем и среднем отношении. Но для двусмежного квадрата точка N не является значимой. Она не отображает ни одного элемента этого квадрата и не определяет значимость параметра b. Двусмежный квадрат, похоже, проявляет себя только как подсобный элемент для нахождения точки N. Если же на базе АС построить два квадрата (показано пунктиром), стороны которых равны долям поделенного отрезка а и с и одна из сторон общая, то на горизонтальной плоскости отобразятся три значащих точки А, В, N. Однако и в этом построении существование параметра b не просматривается.

Точка N делит отрезок АВ на две части (доли), отношение которых в соответствии с (3.33) равно: Ф = ВN/AN = 1,618… или 1/ Ф = АN ⁄ ВN = 0,618…. Однако у нас нет доказательства того, что формализация, описывающая деление отрезка в крайнем и среднем отношении, является единственной и ограничивается только этим делением. Нельзя исключить и того, что за процедурой, определяемой как деление отрезка, скрывается некий способ выявления элементов еще некоторой фигуры (фигур?) «лежащей» на плоскости, например, прямоугольного треугольника. Об этом свидетельствует и то, что в результате преобразования пропорций (3.31) и (3.32) получается уравнение Пифагора (3.35) включающее – гипотенузу с и два катета а и b. Причем появление катета b из уравнений (3.31) и (3.32) оказывается полной неожиданностью. И потому деление отрезка в крайнем и среднем отношении требует дополнительного исследования.

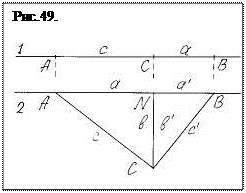Предположим, основываясь на уравнении (3.35), что процесс деления отрезка (то, что процесс ограничивается делением «отрезка», теперь ставится под сомнение), является также процедурой нахождения какой-то выделенной точки некоего прямоугольного треугольника видимого с ребра. Повернем предполагаемую плоскость на 90^о и рассмотрим элементы каких фигур могут оказаться отображенными точками А, В, N (рис. 49.2).

Поскольку отрезок АВ разделен на две части золотым сечением, то можно полагать, что и треугольник, опирающийся на этот отрезок является золотым треугольником. Построим на отрезке равном АВ золотой прямоугольный треугольник АВС, и опустим из вершины С на гипотенузу перпендикуляр СN. Перпендикуляр достигнет гипотенузы в точке N, и поделит треугольник АВС на два подобных золотых треугольника АNС и СNВ. Причем катет СN оказывается общим для обоих треугольников, а сами треугольники «сомкнутыми» (сдвоенными) катетом b = b ´.

Можно подойти к построению золотого треугольника иначе, если в соответствии с (3.36) предположить, что отрезок АВ является диаметром окружности, а точка N – вершина прямоугольного треугольника с гипотенузой АВ, расположенной на горизонтальной плоскости (рис. 50). В этом случае центр окружности О скрыт катетом треугольника и не является значимой величиной. Если принять, что радиус окружности равен, например, R = 5 см, доли отрезка равны АN´ = 6,18 см, ВN´ = 3,82 см, т.е. диаметр, поделен в золотой пропорции: АN`⁄ВN` = 1,618, то можно определить высоту NN` и длину катетов АN = 7,86 см и ВN = 6,18см данного треугольника. Т.е. АN` = ВN. У треугольника АВN высота NN` = 4,86 см, и она пропорциональна отношению | АN ´| ⁄ | NN ´| = Ф = 1,618, а стороны пропорциональны числу Ф. (Покажем это на отношениях модулей сторон: 3,82: 3,82 = 1; 6,18: 3,82 = 1,618; 10,0: 3,82 = 2,618). Следовательно, процедура деления «отрезка» в крайнем и среднем отношении может выявить как точку N на отрезке либо угол АNВ, либо высоту N´N вписанного в окружность прямоугольного треугольника.

Треугольник АNВ носит название золотого степенного треугольника поскольку отношение его сторон пропорциональны числу Ф = (1,272)² = 1,618. Если, например, принять, что у золотого треугольника меньший катет равен Ф ¹ = АN = 1,618 (см), то другой катет равен Ф ² = ВN = 2,618 (см), а гипотенуза Ф ³ = АВ = 4,236 (см). И, следовательно, за процессом делением отрезка в крайнем и среднем отношении может скрываться отображение на горизонтальной плоскости геометрической фигуры – золотого

прямоугольного треугольника обращенного прямым углом N к математику. Процесс же деления выявляет точку схождения катетов этого треугольника и длину его высоты NN ´ = b, а потому и ее размерность (см).

Уравнения (3.31) и (3.32) в этом случае могут относиться к каждому из подобных треугольников, и будут иметь, например, следующий вид:

b ´ = (а´ + с´) ⁄ с´ = с´ ⁄ а´,

b ² = (а + с) ⁄ а = с ²∕ а ²,

при b = b ´,

совместно описывая не деление отрезка в крайнем и среднем отношении, а существование на плоскости сдвоенного золотого треугольника.

Будем полагать, что объяснение наличию пропорций (3.31) и (3.32), и следующего из них уравнению Пифагора, найдено. Но теперь, когда обнаружилось существование, по меньшей мере, двух фигур в одном месте, возникает вопрос, а не скрываются ли там еще и другие фигуры, дополняющие найденные? Тем более, что алгебраическое решение уравнения (3.33) дает два значения числа Ф: Ф = 1,618 и Ф = 0,618 и только одно из них отображается рисунками 49, 50. Возможно, это свидетельствует о том, что полученная фигура золотого треугольника является одним из возможных вариантов решения и нельзя исключить, что существуют другие фигуры, которые отражают два значения величины Ф. Поэтому продолжим рассмотрение возможности отображения отрезком АВ других фигур. Поищем другие варианты.

Можно предположить, например, что точка N есть точка соприкосновения двух смежных окружностей. Построим обе окружности (рис. 51), для чего повторим построение двусмежного квадрата АВСД и нахождение точки N. Проведем диагонали в двусмежном квадрате (показано штрихами) и разделив доли АN и ВN пополам проведем циркулем окружности Б и Б ₁, с радиусами R и r. Обратим внимание на то обстоятельство, что диагональ СВ двусмежного квадрата АСDВ является касательной к окружности Б. Если же теперь «повернуть» окружность Б ₁ вокруг ТТ` как вокруг оси на 180^о, то заняв часть окружности Б, она оказывается касательной к другой диагонали двусмежного квадрата – СВ.

Проведем в каждом из квадратов по диагонали АS и SВ, получив равнобедренный треугольник АSВ, и восстановим из центров окружностей перпендикуляры до пересечения их с окружностями. Точки Е, F пересечения радиусов R и r c окружностями Б и Б ₁будут лежать на диагоналях АS и SВ, т.е. на сторонах равнобедренного треугольника (рис. 51). Если же соединить точки пересечения E и F прямой, то получим разностороннюю трапецию O ₁ EFO ₂. Диагонали этой трапеции пересекаются на перпендикуляре, восстановленном из точки N. Если предположить, что трапеция может «двигаться» деформируясь внутри треугольника АSВ, при постоянном соприкосновении радиусов со сторонами треугольника АSВ, то при ее «движении» влево или вправо, нижнее основание трапеции будет оставаться неизменным. А радиусы окружностей, остальные стороны и диагонали будут пропорционально деформироваться таким образом, что точка пересечения диагоналей трапеции будет всегда находиться на перпендикуляре, восстановленном к диаметру через точки соприкосновения окружностей N. И, следовательно, элементы трапеции и окружности, на которые она «опирается» взаимосвязаны Все элементы фигуры, кроме нижнего основания деформируются пропорционально, при «перемещении» в плоскости равностороннего треугольника АSВ. На рисунке 51 зафиксирован тот миг движения, когда радиусы окружностей относятся друг другу пропорционально числу Ф:

R⁄r = 1,618…, r⁄R = 0,618….

Получаются те же величины отношений, которые извлекаются из решения уравнения (3,33). И потому нельзя исключить, что и фигура на рис. 51 тоже имеет какое-то отношение к делению отрезка в крайнем и среднем отношении, когда точка деления является точкой касания окружностей или точкой пересечения диагоналей разносторонней трапеции. Однако и в этом случае отсутствует размерностная величина b, поскольку отношение радиусов не оказывается размерностной величиной.

Отметим, что наличие двух смежных окружностей, (или сферических образований?) соприкасающихся в одной нейтральной точке как бы моделирует в статике структуру гравитационных полей небесных тел. (Например, структуру Солнца и одной из ее планет, имеющих в качестве нейтральной «точки» – зону одинаковой напряженности своих гравитационных полей.). И структуру молекул (например, структуру молекулы воды) и атомов микромира и т.д. (рис. 19)

Таким образом, процесс деления «прямой» в крайнем и среднем отношении по уравнению (3.31) возможно выявляет существование на горизонтальной плоскости одной из описанных выше фигур (трех параллельных прямых, двух разновеликих квадратов с общей стороной, двусмежного квадрата, двух соприкасающихся окружностей) или, по уравнению (3.35) сдвоенного золотого треугольника с высотой b.

К тому же, как следует из (3.35), деление «отрезка» в крайнем и среднем отношении включает в себя не только видимую (проявленную часть операции − раздвоения первичного отрезка, и результата – появления двух долей–отрезков), но и скрытую, невидимую ее часть (появление прямоугольного треугольника и его катета | NN ´| = b). Невидимая часть может содержать прямоугольный треугольник, с перпендикуляром. Не исключено существование и других фигур: прямоугольников, трапеций, треугольников и окружностей (сфер?). Т.е. одной операцией из двух действий по делению отрезка на две части обусловливается возможность появления нескольких различных фигур, отсутствующих по условиям задачи. Это обстоятельство свидетельствует о существовании в геометрии скрытых фигур (параметров) и неизбежности двойственных результатов некоторых решений (ниже будет показано существование скрытых фигур, например, в проективной геометрии). К тому же элементы всех образуемых на рис. 49-51 фигур оказываются пропорционированными (как бы квантованными) золотому числу Ф или членам числового поля русской матрицы (об этом далее).

Обратим внимание еще на одно очень важное обстоятельство. На появление на рис.51 равнобедренного треугольника АSВ и трапеций, как снаружи фигуры – АСДБ, так и – внутри равнобедренного треугольника O ₁ EFO ₂. Точка S равнобедренного треугольника, лежащая на окружности, как будет показано далее, может оказаться несобственной точкой Дезарга, способной перемещаться по поляре и, следовательно, стороны треугольника АSВ могут приобрести статус параллельных прямых. Наличие же трапеции внутри равнобедренного треугольника как бы обусловливает некое побуждение фигуры к движению, к изменению, к деформации. Фигура трапеции на этом рисунке есть мгновенный снимок из множества тех, которые возникают при ее совместном с окружностями движении, произведенный в тот момент, когда радиусы окружностей оказались пропорционированы по золотой пропорции. И главное, – в этой фигуре просматриваются элементы статико-динамической (полудинамической) геометрии. Геометрии, в которой присутствует «кадрированное время» (дискретизированное по мгновениям), т.е. фиксируются отдельные положения изменяемой фигуры, общее изменение которой можно связать воедино путем построения ряда промежуточных положений (кадров) постепенно преобразующих (деформирующих) одну фигуру в другую. Этими преобразованиями занимается проективная геометрия. Здесь же отметим, что проективная геометрия является частью статико-динамической геометрии, из комплекса первичных фигур которой искусственно удалены многие структурные элементы (искусственное удаление скрыло эти элементы от рассмотрения и усложнило развитие проективной геометрии), и производилось преобразование только одного из них (например, комплекса из четырех гармонических точек). В результате оказалось незамеченным главное, что составляет основу проективной геометрии – ее динамический характер.

Появление нескольких типов фигур, «базирующихся» на сечении отрезка в крайнем и среднем отношении: параллельных Евклида, Дезарга (АSВ), треугольников, трапеций и окружностей обусловливает возможность построения статико-динамической геометрии, в которой могут наличествовать как неподвижные, так и движущиеся фигуры различной структуры, обладающие свойствами системы, с деформирующимися элементами при движении в пространстве изменяемой плотности.

Динамический характер проективной геометрии будет подробнее рассматриваться далее, здесь же остановимся на возможности восстановления целого отрезка, разделенного крайним и средним отношением по одной из его долей-частей. Например, по большей доле (рис. 52.).

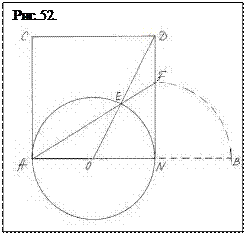Для нахождения полной длины отрезка по его большей части АN построим на этой части квадрат ACДN. Из центра основания квадрата О раствором циркуля проводим окружность, для которой отрезок АN оказывается диаметром. Из угла Д к центру О проводим прямую, пересекающую окружность в точке Е. От угла А через точку Е проводим прямую до пересечения со стороной ДN в точке F и раствором циркуля переносим расстояние FN до пересечения с продолжением прямой АN (показано штрихами) в точке В. Образовавшаяся линия АВ и представляет собой полную длину отрезка до его разделения в крайнем и среднем отношении, а отрезок ВN является его меньшей частью.

После нахождения точки Е построение можно провести другим способом. Через точку Е провести касательную до пересечения с продолжением диаметра АN. Точка пересечения В и отсечет отрезок равный тому, который был до деления в крайнем и среднем отношении.

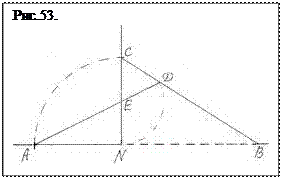Проведем построение полного отрезка, разделенного в крайнем и среднем отношении, по его меньшей части (рис. 53.). На прямой отложим отрезок АN равный меньшей доле первоначального отрезка. Из точки N восстанавливаем перпендикуляр и циркулем переносим на него в точку С длину отрезка АN. Через центр Е отрезка СN проводим прямую АЕ и переносим циркулем на ее продолжение расстояние ЕN. Через образовавшуюся точку Д из точки С проводим прямую до пересечения с продолжением прямой АN в точке В. Образовавшаяся доля NВ и будет большей частью искомого отрезка АВ.

Обобщение:

– Деление отрезка в крайнем и среднем отношении может описываться двумя пропорциями (3.31) и (3.32). Преобразование этих пропорций выявляет некоторые невидимые геометрические фигуры как бы не имеющие отношения к первоначальным пропорциям.

– Появление в результате преобразований (3.31) и (3.32) дополнительного отрезка свидетельствует также о том, что фигуры в динамической геометрии являются системами, у которых все элементы взаимосвязаны. Преобразование уравнения, описывающую данную фигуру в другую форму, вызывает соответствующее изменение самой фигуры или ее элементов.

– Взаимосвязанные элементы фигур наличествуют только в динамических системах, а процедура деления отображает динамику «перемещения» или изменения структуры фигуры.

Обнаружение невидимых фигур при делении отрезка в крайнем и среднем отношении не случайное явление в русской геометрии. Оно свидетельствует о том, что деление есть динамический процесс, отображающий, формализованную в систему взаимосвязь нескольких виртуальных элементов или фигур и их «проявление» в процессе преобразования уравнений. Аналогичные фигуры и свойства пронизывают всю русскую геометрию. Познакомимся с ними подробнее.

Глава IV

Статико-динамическая проективная

геометрия

4.1. Несобственные точки

Дезарга

Выявленные, в процессе рассмотрения задачи деления отрезка в крайнем и среднем отношении, фигуры могут образовывать сами или служить основой для построения множества фигур любой из существующих геометрий: физической (динамической), статико-динами-ческой (похоже, биологической) и статических. Если статические геометрии хорошо изучены и, в частности, статическая геометрия Евклида известна уже более двух тысячелетий, то возможность существования статико-динамической и физической геометрии даже не предполагается. А между тем развитие основ статических геометрий не могло обойти стороной статико-динамическую геометрию. И естественно, что ее элементы не могли не проявить себя при этом развитии. И они проявились. Но в такой форме, что динамика фигур, их деформация и движение оказались скрытыми от рассмотрения, а само движение, происходящее в рамках кадрированного времени, оказалось не обнаруженным. И потому статико-динамическая геометрия получила развитие в форме хорошо известных проективных геометрий. Очень коротко, ориентируясь на [27], рассмотрим некоторые положения проективных геометрий и покажем, что в данных геометриях «неподвижные фигуры» обладают свойством кадрированного движения, характерного для полудинамических систем.

Еще раз отметим, что в статических и в статико-динамической геометриях отсутствует время как свойство тел и потому всякое движение элементов и фигур статико-динамической геометрии отображается как фиксация (стоп-кадр) их пространственного положения в неопределенное мгновение. Сами фигуры в любой фиксированный момент времени неподвижны. Изменение их является кадрированным (как и кадров на кинопленке). Кадр фиксирует изменение (деформацию) в процессе движения фигуры в неопределенное мгновенье.

В статической геометрии, как уже отмечалось, элементы фигур не связаны между собой. Они могут принадлежать или не принадлежать фигуре, существуют вне пространства и времени и остаются неизменными как в фигуре, так и за ее пределами. В статико-динамической (полудинамической) геометрии все элементы фигуры принадлежат фигуре, находящейся между базисами (базисной прямой и точкой опоры), и при изменении положения одного базиса все остальные элементы фигуры пропорционально меняются (деформируют). Фигура в статико-динамической (биологической) геометрии является отдельной системой. Все ее элементы связаны между собой и неотрывны от нее. Фигура всегда находится внутри и под действием некоторого плотностного анизотропного поля. Анизотропное поле образуется как базисом, так и опорной точкой, и фигуры обычно оказываются в плотностном поле одного из них, либо обоих (многих).

Опорная точка есть некоторое отдельное, плотностное образование вроде геометрической гравитирующей точки. По своему геометрическому воздействию на окружающие фигуры опорная точка подобна гравитирующему телу. Фигура, находящаяся в «поле» опорной точки, некоторым образом «взаимодействует» с этим полем. Движение фигуры в поле сопровождается воздействием поля на фигуру, вызывающим ее деформацию и наоборот.

Базисом может являться либо гравитирующая точка, либо линейная последовательность многих близрасположенных гравитирующих точек, которая является аналогом линии, либо плоскость из таких же гравитирующих точек. Базисная «прямая» может представлять собой линию различной кривизны, в том числе и окружность. Причем опорная точка или точки опоры могут находиться как снаружи окружности, так и внутри ее. Пропорционирование фигур и их элементов внутри такой окружности и вне ее производится по общим правилам.

Отметим, что могут существовать фигуры с одним базисом, при этом второй базис как бы потенциально существует на бесконечности. В этом случае сама фигура, вместе с базисами представляет собой единую систему взаимосвязанных элементов или фигур с точкой опоры или без оной, «функционирующую» в определенном анизотропном пространстве и структурно зависящую от положения в нем. Точка опоры S – может быть либо опосредованно точкой (базисная точка), либо плотностной прямой на плоскости, видимой с торца, и всегда является несобственной точкой Дезарга. Изменение положения точки опоры в плотностном пространстве с одной стороны образует новое пространство, отображая иллюзию вневременного движения. А с другой деформирует все элементы перемещаемой фигуры пропорционально структуре создаваемого пространства. Это свойство пропорционального изменения фигуры и ее элементов в зависимости от места расположения точки опоры сохраняется и в том случае, когда элемент «вырезается» (вырывается) из фигуры, проявляя себя как часть базиса. И его деформация при перемещении самого элемента или точки опоры рассматривается вне зависимости от фигуры, из которой он изъят, но по законам пропорционирования фигуры. Более того, сама фигура в этом случае тоже деформирует вместе с вырезанным элементом, но в скрытой форме и процесс этой деформации можно воспроизвести, если даже неизвестна начальная форма фигуры, но сохранилась хотя бы часть ее элементов.

Дата добавления: 2014-12-07