Гармония золотых пропорций 6 страница

Рассмотрим построение на поверхности плоской или объемной фигуры и передвижение ее в пространстве способом пропорционирования. Проведем базисную прямую р и выделим на ней отрезок АД, который произвольно разделим на три части точками В и С (рис. 68). Получили некоторый аналог четырех гармонических точек. Поставим произвольную точку S, соединим ее лучами с точками А, В, С, Д, и посмотрим, что же получилось. Можно предположить, что здесь изображена проективная пирамида в которой точка В проекция поляры на базисную прямую, а точка Д полюс этой поляры. Однако для такой остроконечной фигуры полюс находится неестественно близко. Можно сделать другое предположение: фигура составлена из двух пересекающихся проективных пирамид АSВ и ВSД, каждая из которых включает поляру, а полюса у них – отсутствуют. Наконец возможен и третий вариант: на фигуре изображена четырехгранная пирамида, находящаяся на горизонтальной плоскости.

Допустим, что это четырехгранная пирамида и в произвольном месте пересечем ее плоскостью. Пронумеруем углы образовавшейся площадки 1, 2, 3, 4, и обратим внимание на то, что каждая сторона полученного четырехугольника образует со сторонами пирамиды трапеции: А 12 В, В 23 D, D 34 С, С 41 А. Выше было показано, что продолжение крыши каждой трапеции пересекает базисную прямую, образуя на ней свой полюс. Появление полюса свидетельствует о том, что внутри каждой трапеции существуют диагонали, а вместе с ними и виртуальная поляра. Проявим поляру, например, у ребра АSВ, для чего проведем в трапеции диагонали и через их пересечение проведем прямую – поляру SL (показано штрихами). Далее проведем лучи от крыш до пересечения базисной прямой в точках Е, F, G, Н и отметим, что любое наклонение пирамиды сопровождается деформацией всех ее элементов, но точки полюсов при этом своего положения не меняют и потому становятся реперами. Воспользовавшись этим обстоятельством, поставим произвольно новую точку опоры S _о. Соединим ее прямыми с точками А, В, С, D и перенесем на нее площадку 1234. Перенос можно произвести двумя способами: произвольным способом и пропорционально занимаемому ею месту. Для получения площадки по первому способу следует в нужном месте поставить на одно из ребер наклонной пирамиды АS _о D точку, например, 1´ и, соединив ее лучами с реперами Е и G´, получить стороны 1´2´ и 1´4´. Далее соединив лучами точку 2´ с репером F и точку 3´ с репером Н получить стороны 2´3´ и 3´4´. Искомая площадка 1´2´3´4´ построена.

Чтобы оставить все элементы пирамиды АS _о D пропорциональными АSD, необходимо провести две вспомогательные прямые. Одной соединить вершины S и S ₁, а другую S ₁ K – провести перпендикулярно первой. Затем перпендикулярно прямой S _о K перенести с пирамиды АSD точки 1, 2, 3, 4 на ребра пирамиды АS _о D получить точки 1₁, 2₁, 3₁, 4₁ и соединив их прямыми, найти искомую площадку. Можно наклонить пирамиду и вправо, например, в точку опоры S ₁ провести построение пирамиды аналогично вышеизложенному.

Может возникнуть необходимость пропорционального перенесения площадки 1234 под базисную плоскость пирамиды. Поскольку первая точка искомой площадки может выбираться произвольно, ее ставят на продолжении любого ребра, например, точку 2_о на продолжении ребра SВ и лучами соединяют с реперами Е и Н (рис. 68). Лучи пересекают продолжения ребер АS и SD в точках 1_о и 3_о. Теперь, соединяя лучами точки 1_о и G, получаем точку 4_о, соединив ее с точкой 1_о, находим искомую площадку 1_о2_о3_о4_о. Полученная площадка является видом сверху с базисной плоскости.

Пространственное пропорционирование и перенос плоских и объемных фигур в рамках пирамиды хорошо известен и применяется в начертательной геометрии. Но в ней используется метод пропорционирования относительно сдвинутой базисной прямой или плоскости.

Реперный способ пропорционирования, похоже, неизвестен и не применяется. Естественно, что фигуры, пропорционированные обоими методами, должны быть конгруэнтными. Покажем это на примере пропорционирования той же площадки 1234.

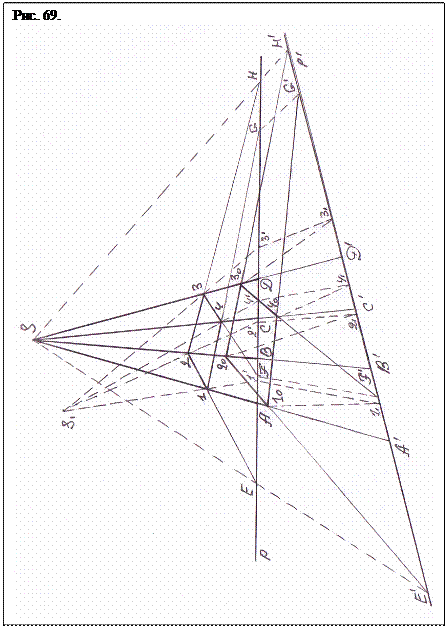
На базисной плоскости р построим прямоугольную пирамиду с основанием АВСD и с вершиной S (рис. 69). Рассечем ее плоскостью 1234. Каждое ребро плоскости можно представить как крышу некоторой трапеции. Перенесем лучами на базисную поверхность р реперные точки Е, F, G, Н, от каждой крыши. Поведем другую базисную плоскость р ´ и продолжим грани пирамиды до пересечения с нею в точках А ´, В ´, С ´, D ´. Проведем через вершину S и точки Е, F, G, Н лучи до пересечения с р ´ в точках Е´, F´, G´, Н´. Реперные отметки перенесены на новую базисную плоскость.

Теперь можно поступать двумя способами: либо, как это изложено в начертательной геометрии, выбрать произвольную вершину S ₁ и провести от нее лучи до пересечения с р. Либо сразу же поставить на одно из ребер пирамиды какую-то точку плоскости, например 1. Выберем вершину S ₁ и проведем от нее лучи (показано штрихами) через точки 1, 2, 3, 4 до пересечения с р в точках 1´, 2´, 3´, 4´. Потом из вершины S проведем лучи через точки 1´, 2´, 3´, 4´ до пересечения с плоскостью р ´ в точках 1₁, 2₁, 3₁, 4₁. Возможность пропорционального перенесения площадки 1234 на другое место подготовлена. Теперь соединим лучам точку S ₁ с точками 1₁, 2₁, 3₁, 4₁ и пересечение их с ребрами А ´ S, В ´ S, С ´ S, D ´ S пронумеруем точками 1_о, 2_о, 3_о, 4_о. Соединив полученные точки прямыми получим искомую площадку 1_о2_о3_о4_о. Теперь через точки 2_о и 1_о, проведем луч до пересечения с плоскостью р´. Луч пройдет через репер Е ´. Проведя аналогичную операцию с точками 2_о и 3_о, получим репер Н ´, с точками 3_о и 4_о, получим репер F ´, с точками 1_о и 4_о, получим репер G ´ (показано на рис. 69 штрихами.).

Таким образом, «площадки» 1_о2_о3_о4_о, перенесенная методом начертательной геометрии и методом реперов, оказываются конгруэнтными.

Не будем останавливаться на пропорционировании объемных фигур методом реперных отметок, поскольку он в принципе повторяет способ пропорционирование плоскостей. Покажем в заключение метод гармоничного пропорционирования вынесенных на оптимальное расстояние за начальную фигуру других плоских или объемных фигур. Этот метод существенен потому, что на сегодня, похоже, отсутствует способ перенесения одной фигуры пропорционально другой и гармоничного сочетания объектов по площади, высоте и объему.

Поэтому застройки городов по высоте, расположению в пространстве и конфигурации объектов представляют безобразное, ангармоничное нагромождение строений, уродующее структуру Земли и разлагающе действующее на психическое здоровье человека.

Еще раз отметим, что гармоничными сооружениями считаются такие объекты, которые по высоте, ширине и длине пропорционированы в золотых пропорциях. Пространственное размещение гармоничных объектов предполагает также использование не измерительных, а соизмерительных инструментов, тех же саженей, как для архитектурного проектирования, так и для размещения их на местности.

Покажем на одном примере пропорциональное перемещение фигуры с одного места на другое, расположенное рядом. Для этого отложим на базисной прямой отрезок АВ = 6 см и разделим его точками А, В, N, D на три части (рис. 22.), причем точка N делит АD в крайнем и среднем отношении. Из точки N восстановим перпендикуляр – поляру, на которой определяем точку опоры S отстоящую от основания на величину, например, равную 9 см. Соединив точку S с точками А и D находим пирамиду АSD, по которой и будет пропорционирована соседняя фигура. Далее следует определить расстояние от пирамиды до соседней фигуры. Оно должно быть кратным золотому числу, например АВ: 2,618 = 3,5 см.

Построение пропорционированной фигуры, отнесенной от пирамиды на расстояние 3,5 см, начинаем с проведения второй базисной прямой р ´, параллельной первой. Поскольку предстоит пропорциоро- ванный «переход» пирамиды АSD на новое место, то следует эту пирамиду «наклонить», перенеся ее точку опоры, например, в точку S _о. И из нее через точки А, В, N, D провести лучи до пересечения с р ´ в точках А ´, В ´, N ´, D ´. Теперь отложим от точки А отрезок АD _о = 3,5 см и через точку D _о из точки D ´ проведем луч, на котором в произвольном месте поставим опорную точку S ₁. Соединим точку S ₁ лучами с точками А ´, В ´, N ´ и в месте пересечения р ´ получим точки А _о, В _о, N _о основания наклонной пирамиды А _о S ₁ D _о. Искомая пирамида А _о S ₁ D _о пропорциональна по вурфу пирамиде АSD. Это можно показать графически. Ранее было показано, что лучи от крыш всех трапеций пропорционированных по вурфу пирамид сходятся в одной точке М. Найдем эту точку для пирамиды АSD. Для этого на поляре возьмем произвольную точку К и от А и D проведем через нее лучи до пересечения с ребрами АS и SD в точках Е и F. Прямая EF − крыша, спроектируем ее на базисную прямую р и получим полюс М. Отметим, что для всех пропорционированных пирамид расстояние от правой точки опоры до полюса будет всегда одинаковым и равным DМ.

Чтобы убедиться в этом построим аналогичную крышу для пирамиды А _о S ₁ D _о и продолжим ее до пересечения с р в точке М _о. Замерим отрезок D _о М _о и получаем, что расстояние ДМ = D _о М _о. Дополнительно проверим это явление. Поставим еще одну точку опоры S ₂ и соединив ее сточками В _о, D _о получаем еще одну пирамиду пропорциональную А ₁ S ₂ D _о. Определим на ней крышу Е _о F _о проведем от нее луч до пересечения с р. Луч пересек р в точке М _о. Таким образом вурфную пропорциональность пирамид А _о S ₁ D _о и АSD можно считать доказанной.

Кратко рассмотрим особенности фигуры называемой «теорема Паскаля». Вот как она описывается [27]:

«Впишем в любое коническое сечение (для проективной геометрии разницы между ними нет) произвольный (произвольный?? – Авт.) шестиугольник (см. рис. 71, на котором стороны занумерованы). Продолжим теперь до пересечения первую и четвертую, вторую и пятую, третью и шестую стороны. Полученные прямые обязательно пересекутся, ибо параллельных в проективной геометрии нет (?? − достаточно сомнительное заявление − Авт.). Итак, мы имеем три точки пересечения трех пар прямых. Вообще говоря, три произвольные точки плоскости не лежат на одной прямой, но эти три − лежат. В этом и заключается теорема Паскаля. Если теперь проектировать коническое сечение вместе с шестиугольником, с точками пересечения его сторон и с прямой, проходящей через эти три точки (ее называют паскалевой прямой), на другую плоскость, то, как бы не изменялось коническое сечение и вся конфигурация, указанные три точки все равно будут лежать на одной прямой. Теорема Паскаля – проективная теорема».

Фигура, изображенная на рис. 71, чуть ли не единственная в проективной геометрии явно отображающая все входящие в ее структуру элементы. А изложенное объяснение ее построения демонстрирует односторонность современного статического подхода к рассмотрению образовавшейся фигуры. Математик, построивший в коническом сечении шестиугольник, полагает, что за пределами шестиугольника ничего нет. И это совершенно правильно, если фигура принадлежит статической геометрии. Но если она относится к проективной геометрии, то сама фигура «знает», что она всего только базисный, опорный элемент единой невидимой фигуры. Вторым элементом является базисная прямая, проходящая за ее пределами и потому попарные лучи, продолженные за пределы сторон шестиугольника обязательно пересекутся на базисной прямой.

Тольков проективном представлении субъекта вписанный в коническое сечение шестиугольник (далее, для упрощения, будем говорить об окружности), является самостоятельной фигурой. В статико-динамической геометрии это несколько неявных фигур-треугольников. Они, частично перекрывая друг друга, наложены на опорную окружность, отсекая своими сторонами шесть хорд, образующих шестиугольник, и составляя вместе с базисной прямой, единую фигуру.

Проведем построение вписанного шестиугольника иначе, чем было описано выше. Возьмем опорную окружность и на некотором расстоянии от нее базисную прямую, на которой находятся точки А, В, С. На окружности расположена точка D, место схождения двух сторон шестиугольника (рис. 72.).

Соединим точки А и С прямыми с точкой D. Точки пересечения Е и F прямых с окружность соединим прямыми с точкой В. Получим новые точки I и L. Из точки С через точку I проведем прямую до пересечения с прямой АD в точке G. А из точки А прямую через L до пересечения с прямой СD в точке Н. Точка пересечения этих прямых К окажется на окружности и замыкает шестигранник. Шестигранник DЕIКLF построен. Он составлен тремя треугольниками АDН, ВFЕ, СDG. Стороны этих треугольников, проходящие внутри окружности, и образуют искомый шестигранник. Он весь включен в треугольник АСD и одновременно, отсекаемыми хордами, вписан в опорную окружность.

Перемещение любого из элементов этой фигуры сопровождается деформацией всех ее элементов кроме базисных. Они же, оставаясь базисными, не испытывают деформации. Базисные фигур испытывают деформацию только тогда, когда перемещаются в другую область пространства. Именно в этом случае окружность, например, отображает коническое сечение.

Покажем деформацию треугольников АНD ВFЕ, и СDG обусловленную перемещением точки В вдоль базисной прямой, допустим влево (показано штрихами). Перемещение В оставило неизменным треугольник АСD и основание треугольника ВFЕ но переместила одну из их сторон (показано штрихами), изменив площадь каждого внутреннего треугольника и точки их пересечения таким образом, что четыре стороны вписанного шестиугольника переместившись по окружности, изменили свою длину, а следовательно, и конфигурация шестиугольника подверглась изменению. Перемещение же точек А и С вдоль базисной прямой, «удаление» или «приближение» к ней опорной окружности, вызывает деформацию всех элементов фигуры, но не сдвинет «произвольные» точки с паскалевой прямой, поскольку эта прямая – базисная.

Таким образом, деформация фигуры в пространстве статико-динамической геометрии, происходящая в результате перемещения отдельных ее элементов или опорных узлов не нарушает структурного единства самой фигуры. Пединим прямыми с точкой В.кружность льника., В, С. описано выше.

Глава V

Элементы физической геометрии

5.1. Физика

в геометрических символах

В физике постоянно дискутируется в физике вопросы о физической сущности свойств: Являются ли геометрические свойства свойствами физическими или эти свойства не имеют отношения к физике? Является ли геометрия самостоятельной наукой со своими свойствами и законами или она есть раздел физики? Ответы на эти вопросы определяются тем представлением о геометриях, которое складывается в науке на протяжении длительного времени, и о связях свойств статических геометрий с физическими свойствами природы. Поскольку до настоящего времени наука оперирует только статическими геометриями, то однозначного ответа на эти вопросы получать не удается. Статические геометрии базируются на аксиомах и теоремах, отсутствующих в природе и получаемых путем абстрагирования от природных свойств. Это обстоятельство обусловливает видимость как бы самостоятельности геометрических свойств, их независимости от природы. Подчеркнем – самостоятельность геометрических свойств. Но является ли статическая геометрия единственным предметом, описывающим геометрические свойства природы? Ниже мы покажем, что классическая геометрия не единственный способ описания геометрии природы. Эти свойства можно описывать и полудинамическим (статико-динамическим) и динамическим методом, что обусловливает возможность лучшего понимания природных процессов. Но продолжим.

Абстрагирование начинается с выделения из природы отдельных свойств, с аксиоматизацией связей между ними и с введением эталонных измерителей количественных параметров этих свойств. При этом практически не учитывается то обстоятельство, что физические свойства невозможно отделить от тел. Они, эти свойства, как уже говорилось, неотъемлемые составляющие комплекса свойств, образующих тела, их атрибуты. Они – в природе никогда не бывают самостью, каждое из них существует в совокупности и только в совокупности всех свойств рассматриваемого объекта. Без любого из свойств материальный объект не существует.

Но для субъекта – ученого – они суть отдельности – мыслимые субстанции, на которых базируется все его представление о природных свойствах, и «выделяются» они из этой совокупности мыслящим субъектом для его практических целей как самостоятельные качества. В природе отсутствуют такие отдельные физические и геометрические свойства, как «расстояние», «плоскость», «пространство», «время» «бесконечность» и т.д. К тому же свойства: расстояние, плоскость, пространство, бесконечность находят применение и в физике и в геометрии свидетельствуя, таким образом, о некоей неразрывности понятий физики и геометрии. Тем не менее, представления об этих свойствах в физике и в статической геометрии могут оказаться различным. И то, что оно сейчас необъяснимо совпадает, свидетельствует о недостаточном представлении сущности физических и геометрических свойств.

В основе всех представлений геометрических свойств, как уже неоднократно подчеркивалось, заложено понятие о пространстве. И в первую очередь о вещественности этого пространства. Многократно повторимся. Невещественность пространства – есть пустота, в коей ничего нет, и по определению быть не может. Пустота – категория непостижимая для ума, т.к. в любом построении ум субъекта обязан быть «наблюдателем». А как «оказаться» в месте, в котором ничего нет? И что можно сказать о нем? Только одни отрицания: неподвижный, невещественный (бестелесный), не пространственный и т.д. и т.п. А нет пространства, нет и эталона для его измерения.

Однако, по укоренившейся традиции, такой неподвижной, невещественной, примысливаемой пустоте приписывают свойство самость – пространство и существование некоего расстояния между примысливаемыми в нем телами, которое замеряют размерными эталонами, в частности – метром. Но метр – вещественный эталон. И в его современной формулировке заложены два основных признака вещественности – материальность и движение. Ответ на вопрос: − Как можно замерять невещественное (примысливаемая пустота) вещественным? − естественно отсутствует. И бессмысленная традиция сохраняется. Однако во всех мировых философиях имеется тезис «подобное взаимодействует с подобным» и только в физике этот тезис нарушается, поскольку получается, что пустота, не имеющая свойств тел, и, следовательно, не подобное телам, вмещает совокупности свойств – тела, а отсутствующая в пустоте протяженность замеряется протяженным телом. Попробуем еще раз определиться с пространством и расстоянием в физике и геометрии.

Естественно, что необходимость выживания и ориентации человека в жизненном пространстве породила понимание реального (вещественного) пространства и расстояния как протяженности, как промежутка между телами, задолго до того, как у него появились даже самые первичные представления об измерениях и числах. И это представление определялось не выделением свойства из общей совокупности, а сопоставлением свойства отдельного предмета с таким же свойством другого подобного предмета, принимаемого за эталон. И потому измерение промежутков можно было проводить только посредством применения имеющихся тел, используя их в качестве эталонов. Первоначальные эталонные измерительные инструменты, как предполагается, не базировались на параметрах Земли, и, более того, ничем не были связаны с физическими параметрами, а для определения протяженности использовались некие практические факторы. Например, расстояние у греков определялось по дальности падения брошенного копья, у кочевников по дальности полета стрелы и т.д. Т.е. развитие представлений о пространстве и расстоянии происходило от частного к общему. И логика этого развития привела к формальному, опосредованному пропорционированию размеров эталонного измерительного инструмента, названного метром, параметрам Земли. Произошло чисто механическое пропорционирование инструмента по измерению расстояния – метра, параметрам планеты, а потому физическая сущность понятия «расстояние» оказалась не выявленной. Попробуем прояснить, что же лежит в основе физического понятия – «расстояния» как категории, на которой основывается вся геометрия.

Если за отправную точку рассуждения принять предположение о том, что космос отображает пространство, то обращает на себя внимание визуально «наблюдаемая» изотропность космического пространства. Имеется ли в действительности изотропность – пока неизвестно, хотя в соответствии с диалектикой пространство вещественно и, следовательно, анизотропно. Но в космосе наличествуют выделяющиеся на общем, как бы безматериальном фоне отдельные вещественные тела – планеты, звезды, галактики и т.д. Т.е. тела, имеющие большую, против остального пространства, массу и плотность.

Эти выделенные тела влияют, через пространство (добавим, вещественное, иначе как может это влияние передаваться), друг на друга гравитационными полями. Энергия последних убывает по мере отдаления от самих небесных тел. Убывание энергии гравитационных полей с расстоянием однозначно свидетельствует об анизотропии космического пространства и о том, что плотность энергии вблизи тел больше, а в отдалении меньше. И еще о том, что где-то между взаимодействующими телами существует зона одинаковой гравитационной энергетической плотности (нейтральная зона). Все объекты, находящиеся между двумя гравитирующими телами, под воздействием их полей изменяют свою форму – деформируют [2]. Уменьшаются или увеличиваются в размерах в зависимости от того, находятся ли они ближе к гравитирующему телу или дальше от него. Причем в движении от одного плотного тела к другому до нейтральной зоны они увеличиваются в размерах, а после прохождения ее – уменьшаются пропорционально энергии того тела, к которому они приближаются. Этой деформации подвержены все тела без исключения, в том числе «твердые» эталоны.

Свойство деформации плотностного тела в физическом пространстве и отображает статико–динамическая геометрия. В ней фигуры, как и свойства тел природы, есть – взаимосвязанная совокупность всех элементов, составляющих фигуру, т.е. отдельное. В дискретном (дуальном) мире телам присуща внутренняя целостность, но отношение с другими телами переводит целостность в отдельность. Ни один элемент отдельной фигуры из нее изъять невозможно, так же как невозможно изъять из тела ни одного его свойства. Удаленный из фигуры элемент, тем не менее, в скрытом состоянии, остается в ней так же, как рассмотрение отдельных свойств тела не свидетельствует о том, что тело исчезло. Это обстоятельство и обусловливает наличие в статической (?) и статико-динамической геометриях скрытых фигур. По аналогии можно отметить, что свойства, не учитываемые в физических расчетах, остаются скрытыми в комплексе совокупности свойств тела.

Анизотропная плотностность геометрического пространства обусловлена тем, что все точки пространства статико-динамической геометрии имеют статус несобственных, т.е. плотностных точек Дезарга. Причем плотностность всех несобственных точек различна. Наибольшую плотностность имеют точки, образующие базисные фигуры. Плотностные базисные фигуры – опорная точка и базисная плоскость, своеобразно отображают в геометрии свойства тел, создающих гравитационные поля. Они «создают» некоторое анизотропное, изменяемое с расстоянием плотностное пространство статико-динамической геометрии. Под воздействием этих невидимых «геометрических полей» находящиеся в них фигуры деформируются. Все элементы фигуры, передвигающейся между плотностной точкой опоры и такой же базисной линией (базисной плоскостью) деформируются пропорционально плотности того геометрического пространства, в которое они попадают, возрастая по длине при удалении от плотностных точек и уменьшаясь с приближением к ним.

Естественно, что в статико-динамической геометрии отсутствуют реальные плотности, энергии, расстояния и силовые деформации. Имеется своего рода проективное отображение плотностного пространства, протяженности и взаимодействия фигуры с пространством. Именно оно вызывает пропорциональное изменение размеров элементов фигуры при движении на плоскости геометрического листа как некоторое подобие реальных физических процессов. Эти фиктивные для геометрии плотностные свойства, тем не менее, моделируют природные процессы в пространстве статико-динамической геометрии. При этом в отображении протяженности используется общая для всех геометрий и физики методика измерения длин и расстояний и единый эталонный измерительный инструмент. Например, метр. Но измерительный эталон вещественная величина. Чтобы им пользоваться в статико-динамической геометрии надо определиться с физическими свойствами протяженности, обусловливающими появление геометрического понятие «расстояние».

Обратимся к телу, например, к Земле и определимся, можно ли из совокупности ее свойств определить те физические свойства, которые образуют геометрическое понятие «расстояние», и какие взаимосвязи они создают. В первом приближении Земля – шар. Параметры шара включают его радиус и поверхность. Радиус и есть «расстояние» от поверхности до центра Земли. Возникает вопрос: Совокупность каких «отдельных» физических свойств планеты определяет длину радиуса?

Радиус Земли R определяется через ее частоту пульсации (угловую скорость?) ω и скорость v вращения гравитационного поля, равную первой орбитальной скорости:

R = v⁄ω, (5.1)

частота пульсации пропорциональна периоду Т:

ω = 1 ⁄ Т, (5.2)

и, подставляя в (5.1) вместо ω из (5.2) 1 ⁄ Т имеем:

R = vТ. (5.3)

Т.е радиус Земли «определяется» не эталонным инструментом длины, а физическими свойствами некоторого колебательного процесса (периодом или частотой) и скоростью его распространения, и, следовательно, измерительный инструмент, используемый для измерения должен обладать подобными свойствами. Отметим; параметры окружности Земли по поверхности L, как и ее площади S тоже включают в себя колебательный процесс и длину волны λ_з планеты:

L = 2 πR = 2 πvТ = λ _з, (5.4)

S = 4 πR ² = πv ² Т ². (5.5)

И это естественно, поскольку все тела, как и эталонные измерительные инструменты, физически пульсируют [2]. Пульсация, как и все остальные свойства, – атрибут каждого тела и отдельно от тела не существует, но может передаваться через вещественное пространство другим телам. Так передаются, например, электромагнитные и гравитационные волны.

Дата добавления: 2014-12-07