Гармония золотых пропорций 5 страница

Пары слева от поляры:

1) АМ ´ + ВМ ´ = С ₁´ Д ₁´ = 100; 1´) АN ´ + ВN ´ = АВ = 10. (4.10)

2) АМ ´´ + ВМ ´´ = С ₂´ Д ₂´ = 33,34; 2´) АN ´´ + ВN ´´= АВ = 10. (4.11)

3) АМ ´´´ + ВМ ´´´ = С ₃´ Д ´₃ = 23,82; 3´) АN ´´´ + ВN ´´´= АВ = 10. (4.12)

Еще раз отметим, что пропорциональность сдвоенных рядов обеспечивает коэффициент, получаемый делением каждого верхнего числа на нижнее. В частности, для ряда 3)-3´) этот коэффициент равен 2,382. Каждый последующий член ряда, по методу Фибоначчи, равен сумме двух предыдущих. А отношение двух соседних чисел ряда синхронно приближаются к Ф. Таблица 5 отображает эту синхронность. Приближение к числу Ф показано и над числами первого ряда, и под числами второго ряда.

Таблица 5

2,447; 1,408; 1,710; 1,585; 1,631; 1,6131; 1,6199; 1,617

6,91; 16,91; 23,82; 40,73; 64,55; 105,28; 169,83; 275,11; 444,94;

2,9; 7,1; 10; 17,1; 27,1; 44,2; 71,3; 115,5; 186,8;

2,448; 1,408; 1,710; 1,585; 1,631; 1,6131; 1,6199; 1,617

Внутреннее родство сдвоенных рядов подтверждается и методом вурфа. Если в уравнение (4.2) подставить числа парных рядов, то для каждой пары будет получен одинаковый вурфный коэффициент. Покажем это для пропорции образуемой с точками М и N:

W _{1 а} = (ВМ + АМ) (АМ + С ₁ Д ₁) ⁄ АМ (ВМ + АМ + С ₁ Д ₁) = 1,309 = Ф ²⁄2.

W _{1 б} = (ВN + АN) (АN + АВ) ⁄(ВN + АN + АВ) = 1,309 = Ф ²⁄2.

Найдем попарные вурфы других рядов:

W _{2 а} = 1,156; W _{2 б} = 1,155; W _{3 а} = 1,074; W _{3 б} = 1,074;

W ₁ = 1,409; W _1´ = 1,409; W ₂ = 1,269; W _2´= 1,269;

W ₃ = 1,074; W _3´ =1,074.

Разная величина вурфных отношений, каждая для своей пары, тем не менее, не препятствует, как будет показано далее, пропорционированию всех точек в единую взаимосвязанную комбинацию. Отметим, однако, что пропорциональные отсекаемым отрезкам величины серии СД, являющиеся параметрами некоторых неявных гармонических точек на базисной прямой, вообще не используются в проективной геометрии. Это обстоятельство скрывает объективную пропорциональность всей системы образуемых отрезков и их попарную аналогию с первой тройкой чисел рядов Фибоначчи. Кроме того, наличие этих рядов свидетельствует о том, что образующаяся система пропорциональных гармонических отрезков отображает динамические процессы в проективной геометрии. Как явствует из (4.5)-(4.6) любое статическое положение поляры на диаметре фигуры обусловливает появление некоторой серии гармонических точек отсекающих на базисной прямой, за пределами окружности, симметричные и несимметричные попарно пропорциональные отрезки. Последние и формализуются в виде (4.7). С проявлением парных пропорций и с возрастанием количества точек на базисной прямой значительно расширяется структура пропорционирования отрезков.

Как уже было показано, основное уравнение гармонической четверки точек в проективной геометрии имеет следующий вид:

АN ⁄ ВN = АМ ⁄ ВМ

Оно может преобразовываться в следующую форму:

АN·ВN ⁄ АМ·ВN = 1. (4.13)

Отметим, что отношение (4.13) – многозначная пропорциональность, приравненная базисной 1, – основа памяти чисел и теории физической размерности. Она обусловливает нахождение любого неизвестного члена уравнения по трем известным. Базисная единица есть безразмерностная константа в математике, и в частности особым (центральным или базисным) числом в русской матрице, а в физике может быть как размерностной, так и безразмерностной единицей, связывающей переменные параметры одной системы. Именно она отображает динамику (бесконечное движение) свойств одной системы как в статико-динамической, так и физической (динамической) геометрии. Пропорциональное изменение переменных параметров в аналогичной форме физических уравнений не оказывает влияния на базисную единицу. А поэтому аналоги (4.13) в физике, как и в статико-динамической геометрии являются инвариантами.

Поскольку у ряда Пилецкого существует коэффициент, то использование его и золотых коэффициентов взаимосвязи обусловливает появления ряда других пропорций:

АМ ⁄ АN = ВМ ⁄ ВN; АМ ⁄ АN = СД ⁄ АВ; ВМ ⁄ ВN = СД ⁄ АВ;

АМ ⁄ ВМ = СД ⁄ АМ; АМ ⁄ВN = СД ⁄АN; ВМ ⁄ АN = АМ ⁄АВ; и т.д.

Могут появляться и такие, экзотические для проективной геометрии, пропорции модулей отрезков:

| АN |² ⁄ | ВN |² = ВМ ⁄ АN; | ВМ |² ⁄ | АN |² = АМ ⁄ ВN; (4.14)

| АМ |³⁄ | ВМ |³ = ВМ ⁄ ВN; | АN |⁴ ⁄ | ВN |⁴ = АМ ⁄ ВN; и т.д.

Все пропорции модулей могут быть скомпонованы по единой форме и приравнены к базисной единице:

АМ·ВN ⁄ АN · ВМ = 1; АМ·АВ ⁄ АN · СД = 1;

| АN |³ ⁄ | ВN |²· ВМ = 1; | ВМ |²· ВN ⁄ | АN |² · АМ = 1; (4.15)

| АМ |³· ВN ⁄ | ВМ |⁴ = 1; | АN |⁴ ⁄ | ВN |³· АМ = 1; и т.д.

Базисная единица, стоящая в правой части каждого уравнений (4.13)–(4.15), свидетельствует, что сложные отношения множества модулей пропорционально сбалансированы. При дальнейшем движении поляры точки серий М и N тоже передвигаются, но величина каждого модуля изменяется таким образом, что их пропорциональность базисной единице сохраняется. Эта сбалансированность сохраняется и в том случае, когда отношения модулей приравниваются друг другу через их равенство базисной единице:

АМ·ВN ⁄ АN · ВМ = АМ·АВ ⁄ АN · СД;

| АN |³ ⁄ | ВN |²· ВМ = | ВМ |²· ВN ⁄ | АN |² · АМ; (4.16)

| АМ |³· ВN ⁄ | ВМ |⁴ = | АN |⁴ ⁄ | ВN |³· АМ;

Пропорции типа (4.16) можно подвергнуть дальнейшим преобразованиям и приравнивать базисной единице:

АМ·ВN · АN · СД ⁄ АN · ВМ · АМ·АВ = 1;

| АN |⁵· АМ ⁄ | ВN |³· | ВМ |³ = 1; (4.17)

| АМ |⁴·| ВN |⁴⁄ | ВМ |⁴·| АN |⁴ = 1; и т.д.

Процесс компонования пропорцией базисных уравнений может, по-видимому, продолжаться до тех пор, пока не охватит все параметры, входящие в структуру рассматриваемой фигуры. Это возможно потому, что в полудинамической геометрии все параметры взаимосвязаны и с изменением формы фигуры в движении все они деформируют, сохраняя, однако, взаимную пропорциональность. Это природное качество – сохранение взаимосвязей всех свойств тел при деформациях и отображает статико-динамическая геометрия. Члены базисных уравнений могут образовывать как простые пропорции, так и пропорции связанные с числами Фибоначчи и с золотым числом Ф.

Золотые числа проявляют себя в движении в статико-динамической геометрии как три числа начала ряда Фибоначчи в потенции к образованию геометрической прогрессии и с переходом к золотым матрицам.

4.4. Двойственность точка – прямая

Остановимся на операции замены прямых точками или точек прямыми в проективной и в статико-динамической геометрии и определим, какова разница в зависимости геометрических образов этих геометрий даже при одинаковом подходе к пониманию одних и тех же операций. Операция замены точек прямыми, а прямых точками является процессом преобразования элементов фигуры одного вида в другой. При этом сохраняются некоторые существенные качества первой фигуры. Замена хорошо отработана в проективной геометрии, вытекает из того эмпирического обстоятельства, что замена каждой плоскости или прямой некоторой фигуры на точку и последующее соединение этих точек образует другую фигуру, в известной степени отображающую первую. Используя то обстоятельство, что в проективной геометрии все прямые пересекаются, и каждая пересекается с другой в единственной точке, французский геометр Понселе предложил «принцип двойственности» [27]:

«…из каждого проективного предложения относительно точек и прямых на плоскости может быть получено второе предложение путем замены слова «точка» словом «прямая» и наоборот».

А для понимания процесса приведения в соответствие точек и прямых введен термин «инцидентность». Так, если прямая и точка инцидентны, то либо точка лежит на прямой, либо прямая проходит через точку. Поэтому две различные точки инцидентны одной (единственной) прямой, или две прямые инцидентны единственной точке. Рассмотрим приведение в перспективное соответствие точек и прямых на примере фигур изображенных нарис. 7 и 8 работы [27]:

«Простейшая связь между точкой и прямой – перспектива. Она приводит в соответствиеточкам А, В, С, Д … одной прямой (l) точки А´, В´, С´, Д´, … другой прямой (l´), а также пучок прямых а, b, с, д, … с центром в S (рис. 63).

Заменим теперь прямую l точкой L, прямую l` точкой L`, точку S прямой s, а точки А, В, С, Д… и А´, В´, С´, Д´… прямыми а, b, с, д … и а´, b´, с´, д´…, как это сделано на рис.64., т.е. применим принцип двойственности.

В первом случае два точечных ряда приведены в соответствие при помощи пучка прямых. Во втором – два пучка прямых приведены в соответствие при помощи точечного ряда. Оба соответствия называются перспективными».

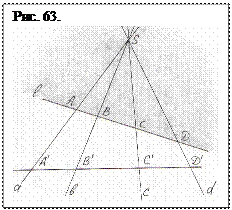Отметим, что в статико-динамической геометрии точка и прямая обладают различными качествами и потому прямая никогда не может проходить через точку. Точка, это нечто напоминающее черную дыру, которая «впускает» прямую, но из себя не выпускает. Прямая – всегда последовательность впритык расположенных несобственных точек другого ранга. Лучи же прямыми не являются. Они виртуальные, подсобные части необходимые для выявления взаимосвязей элементов фигур. В статической геометрии точка, и прямая равнозначны и равнокачественны. Именно это обстоятельство и становится формальным обоснованием возможности замены точки на прямую и обратно. Рассмотрим, что же получилось на рисунках 63, 64? Прежде всего, рисунки 63 и 64 выполнены по законам статической геометрии и при выполнении их не принимается во внимание скрытая двойственность фигур, и не учитывается существование несобственных точек и плоскостей. На рис. 63 смотрятся только прямые и точка S, в которую «входит» пучок лучей, проходящих через эти прямые. Однако рис. 63 – копия рис. 8 [27] отображающего перенос гармонической четверки точек с одной прямой на другую. Выше же показано, что точка S является точкой опоры, а прямая АД – базисной прямой. Последнее изменяет смыслрис. 63, обусловливая соразмерность четырех точек на базисных прямых l и l´. Эта соразмерность главный элемент фигуры, и ее необходимо получить на прямой (рис. 64).

Однако не исключено, что на рисунке 15 изображены две плоскости, на которых проведены лучи от l и l ´, пересекающиеся в точке S. При этом лучи плоскости, на которой находится прямая l, покрывают часть лучей плоскости, на которой находится прямая l ´, что отмечено на рис. 63, затемнением плоскости АSД. Схема, полученная на рис. 63, с опорой на евклидову геометрию, обусловила появление искажения при замене прямых точками нарис. 64. Рисунок исполнен в данной работе уже с учетом того, что на рис. 63 изображено пересечение плоскостей в точке S, и лучи, находящиеся под верхней плоскостью выполнены штрихованными (в работе [27]они не штрихованы). На этом рисунке видно, что прямая S является следом пересечения плоскостей, на которых находятся точки L и L ´.

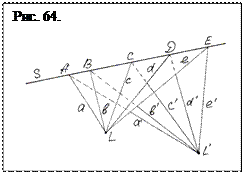От этих точек нет логического перехода к прямой s и потому «гармонические» отрезки на прямой S получены случайным образом, а не перенесены с рис. 63 и потому не могут считаться гармоническими. Наличие гармонических отрезков на рис. 63 и должно являться ее существенным признаком. Отсутствие четырех гармонических точек прямой s свидетельствует о том, что фигура на рис. 64 не является отображением фигуры рис. 63. Да и обозначения точек на ней просто перенесены с прямой l рис. 63, тогда как должно быть: А _о, В _о, С _о, Д _о. Таким образом, проведенная операция замены прямых точками и наоборот не может считаться корректной и скорее представляет не замену прямых точками, а точек прямыми, а выполненный с искажением поворот элементов фигуры рис.63 на некоторый угол. При этом прямая s нанесена на плоскость под некоторым углом, прямые l и l ´ входят в эту плоскость под прямым углом, а лучи а, b, с, д … и а´, b´, с´, д´ …,только выглядят входящими в точки L и L ´, оставаясь гармоническими на видимых с торца прямых l и l ´.

Отметим еще раз, что на каждом из рисунков 63 и 64 изображены, как минимум, два вида фигур. За каждым лучом, исходящим из некоторой точки на прямой, может располагаться другой луч и, возможно, не один, который может проявить себя, когда прямая превращается в точку и наоборот. Поэтому в опорной точке S (рис. 63) могут сходиться четыре пространственных луча, разделяющие базисные прямые l и l ´ на гармонические отрезки. Прямые l и l´ не просто прямые, а прямые базисные и отображают они гармонические точки базисной плоскости, плоскости – все точки которой несобственные. И лучи-прямые, «исходящие» из точки опоры S, не пересекают их, а только отмечают те места базисной плоскости, которых они касаются. И, следовательно, на рисунке 63 отображен перенос базисной прямой l в прямую l´. Другой вариант, в соответствии со статической геометрией, в точке S пересекаются две поверхности, на которых расположены прямые l и l ´, от которых к точке пересечения сходятся по две пары лучей. И чтобы заменить евклидову точку на прямую, достаточно предположить, что прямая на рис. 63 «входит» в плоскость. «Поворот» плоскости на некоторый угол выявит наличие этой прямой.

В статико-динамической геометрии опорную точку Дезарга превратить в прямую невозможно. Это не фигура статической геометрии. Большинство точек Дезарга образуются в визуально видимом конусе лучей, сходящихся в точку под «острым» углом. Никакие повороты плоскости не отобразятся на плотностных точках Дезарга, они только «перемещают» эти точки на иной градус относительно плоскости. Но точка Дезарга может быть представлена в виде множества точек расположенных на несобственной плоскости и образующих базисную прямую. И на эту базисную прямую, по принципу двойственности, можно перенести гармоническое пропорционирование четырех точек с любой прямой, например, с l или l ´. Следовательно, прямые l и l ´ на рис. 63 оказываются не евклидовыми, а базисными прямыми. При замене их точками они превращаются в базисные точки опоры L и L ´.

Отметим, что в соответствии со статико-динамической геометрией, точка S на рис. 63 является опорной точкой, а прямые l и l ´ базисными прямыми пропорционированными четверкой гармонических точек. На этом рисунке,аналогичномрис. 56,отображена деформация расстояний между гармоническими точками, обусловленная удалением базисной прямой от точки опоры S. Естественно, что с начального состояния l в мгновенном процессе этого перемещения происходило бесчисленное количество «рывков» и «остановов» прежде чем было достигнуто положение l ´. Ведь это мы, по своему усмотрению, проявили здесь первый и последний кадры прошедших деформаций. И в этих кадрах незримо, не проявлено в движущемся отображении, присутствуют как элементы фигурной системы: и окружность, и трапеция, и касательные и поляра, вне зависимости от того изображены ли они на рис.63 или нет.

Теперь имея первоначальный вариант фигуры рис. 63 можно заменить точку опоры S множеством опорных точек образующих прямую s на несобственной плоскости (рис. 65.). Прямая s становится новой базисной прямой, на которую и следует перенести с прямой l либо l ´ гармоническую четверку точек. Для проведения этой операции необходимо в любой удобной точке пространства выбрать вспомогательную точку опоры S ₁ (поскольку все пространство образовано несобственными точками) и от нее через точки А, В, С, Д или А ´, В ´, С ´, Д ´ провести лучи до пересечения с базисной прямой s (показано штрихами). Получаем на базисной прямой s новый ряд гармонических точек А _о, В _о, С_о, Д _о (рис. 65). Заменяем базисные прямые l и l ´ на опорные точки L и L ´ расположенные напротив своих прямых (правильнее – расположенных на своих виртуальных прямых, поскольку прямые заменены точками в тех районах, по которым они проходили) и соединяем их лучами с точками А _о, В _о, С _о, Д _о. Построение закончено. Два точечных ряда А ´, В ´, С ´, Д ´ и А _о, В _о, С_о, Д _о приведены в соответствие пучкам прямых точек L и L ´.

Образовавшаяся сдвоенная фигура (две наклонных проективных пирамиды) оказывается подобной двум кадрам пирамиды Дезарг (вертикальной и наклонной), отображенной на (рис. 59), только изображена она под базисной прямой. А это, по-видимому, означает, что данная фигура представлена двумя кадрами, изображающими состояние проективной пирамиды в различные промежутки времени. При этом кадр с вершиной L предшествует кадру с вершины L´, перемещались эти вершины по определенной траектории в пространстве под базисной плоскостью. А их основание не подвергалось перемещению. Простейшей траекторией движения вершины L может оказаться прямая соединяющая LL´.

И в то же время, если рассматривать полученную фигуру с позиций классической геометрии, на рисунке 65 изображен поворот двух пересекающихся по линии А _о Д _о плоскостей с расположенными на них точками LL ´ и лучами а, b, с, д … и а´, b´, с´, д´ ….И образованная фигура как будто бы повторяет фигуру изображенную на рис. 64, но смысл их различен. Точка на рис. 64, являясь евклидовой прямой, видимой с торца, и все лучи от базисной прямой

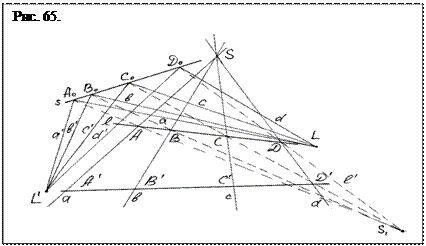попадают на эту прямую в разных местах ее. Точки же на рис. 65 являются несобственными точками и в них сходятся все «приходящие» к ним лучи. Похоже, что операция замены точек прямыми, а прямых точками, сопровождаемая изменением качества элементов образующих фигуру и сохранением одного из ее важных признаков, возможна только в статико-динамической геометрии.

Рассмотрим в соответствии с [27],способ нахождения перспективы переводом одного ряда в другой:

«Итак, возьмем прямую р и на ней точки А, В, С и Д. Измерим длины отрезков АС, СВ, АД, и ДВ. Подсчитаем сложное отношение (АВ; СД). Полученное число обозначим q. Итак,

(АВ; СД) = (|АС |.⁄|СВ|) ⁄(|АД| ⁄|ДВ| = q.

Возьмем другую прямую р´ и на ней три точки А´, В´, С´ (рис. 66) Проведем прямую через точки А и А´ и на этой прямой выберем произвольные точки S₁ и S₂, которые объявим центрами искомых перспектив. Проведем прямые S₁В и S₂В´ и точку их пересечения обозначим В_о. Затем проведем прямые S₁С и S₂С´. Они пересекутся в точке С_о. Точки С_оВ_о определяют прямую u, ее мы назовем осью перспективы. Если теперь провести прямую S₁Д, то ее пересечение с осью перспективы даст точку. Д_о, причем ясно, что по свойству перспективы (А_оВ_о; С_оД_о) = q. Соединим теперь точку Д_о с точкой S₂. На прямой р´ появилась точка Д´. Сложные отношения (А´В´; С´Д´) и (А_оВ_о; С_оД_о) равны. Следовательно равны и сложные отношения (АВ; СД) и (А´В´; С´Д´) (транзитивность!). Дальше построение можно было вести так: на прямой р взять пятую точку Е и, проведя S₁Е, отметив Е_о, соединив Е_о с S₂, получить пятую точку Е´ на прямой р´. Очевидно, (АВ; СЕ) = (А_оВ_о; С_оЕ_о) = (А´В´; С´Е´). Продолжая в том же духе, мы получим один проективный ряд из другого двумя перспективами».

(Примем во внимание, что установить проективное соответствие можно было бы и по трем парам гармонических точек. Двух пар для этого недостаточно.)

Полученная фигура (рис. 66) представляет собой вид сверху и потому кажется выполненной на плоскости. Однако наличие двух опорных точек S ₁и S ₂, разнесенных по разные стороны базисных прямых, свидетельствует о том, что фигура образована в простран-стве, а прямые р и р ´ и точки А, В, … и А ´, В ´, … и т.д. на них, соединенные лучами с опорными точками, оказываются расположенными на разных плоскостях. Об этом же свидетельствует прямая, соединяющая опорные точки. А поскольку эта прямая проходит также через точки А и А ´ то они лежат на одной плоскости с опорными точками и плоскость эта пересекает все три прямые.

Появляется две возможности: одна – определить конфигурацию образованную тремя прямыми, а уже потом заменять прямые и точки, другая – сразу начать замену прямых точками, а точек прямыми. Поскольку нас интересует только замена, проведем один из ее возможных вариантов (рис. 67). Сначала заменим опорные точки базисными прямыми s ₁ и s ₂ любого направления удобного для перенесения на них сложного отношения четырех точек. Затем заменим одну из прямых опорной точкой, например, Р и проведем от нее лучи (показано штрихами) через точки либо прямой u, либо прямой р´ (оставлены точки без индексации) до пересечения с прямой s ₂ в точках А ₁, В ₁, С ₁,

Д ₁. После этого можно заменить оставшиеся прямые u, и р´ точками U и Р ´. Затем из точек А ₁, В ₁, С ₁, Д ₁ прямой s₂ через, например, точку U проведем лучи до пересечения с прямой s₁. Образовавшиеся на прямой s₁ точки А ₂, В ₂, С₂, Д₂ и составят четверку гармонических точек. Далее повторим аналогичную процедуру с точкой Р ´, проведя через нее лучи либо с точек А ₁, В ₁, С ₁, Д ₁ А ₁ прямой s₂, либо с точек А ₂, В ₂, С₂, Д₂ прямой s₁ (последняя операция не отображена на рисунке 67). Построение закончено. Посредством замены точек прямыми и прямых точками два проективных ряда получены двумя перспективами

4.5. Гармоническое пространственное

пропорционирование

Гармоническим пропорционирование можно назвать такое пропорционирование, которое обусловливает параметрам любого проектируемого объекта совокупную соразмерность с параметрами Земли. (Совокупная соразмерность – взаимосвязанная соразмерность по высоте, ширине и длине.) На первый взгляд кажется, что предъявляемое требование к пропорционированию объекта, по меньшей мере, завышено, ибо размеры каждого объекта несоизмеримы с размерами Земли. И данное требование невыполнимо. Но это по первому взгляду.

Отметим: система соизмерительных инструментов, обеспечивающая пропорционирование параметрам Земли любых возводимых объектов использовалась на Древней Руси и у многих других древних народов. Она представляла собой комплекс соизмерительных инструментов – саженей и на сегодня утрачена. В частности на Руси существовал «Всемер» из пятнадцати саженей переоткрытый А. Пилецким (см.приложение 2). Методика очертания объектов по данным саженям полностью утеряна и только начинает воспроизводиться. Главное в ней то, что сажени не измерительные, а соизмерительные инструменты, и все они между собой пропорциональны золотому числу Ф. Поэтому сооружение, проектируемое по комплексу саженей, изначально закладывались в золотых пропорциях, а разметка объемов производилась так, что высота разбивалась саженью одного размера, ширина – сажень другого размера, а длина – третьего размера. В результате строительство каждого объекта велось в гармоничных золотых пропорциях, т.е. в тех параметрах, которые пропорционированы параметрам Земли.

В данной работе не будем останавливаться на методах гармонического проектирования и строительства, кое-что об этом можно найти в [23], здесь же качественно познакомимся с некоторыми проективными способами проведения пропорционирования фигур на плоскости и в пространстве. При этом надо помнить, что исходным пунктом всякого гармоничного пропорционирования является использование золотых пропорций. Гармоничное пропорционирование это всегда пропорционирование на основе золотых пропорций. В проекте строительства объекта высота, ширина и длина должны быть выполнены пропорционально золотому числу или золотым числам, т.е. в соответствии с методом проектирования на основе древнерусских саженей.

Остановимся на возможности гармонизации фигур в статико-динамической геометрии. Еще раз отметим, что в проективной полудинамической геометрии фигуры пропорционированы изначально как системы, способные кадрировано деформироваться в процессе перемещения в пространстве. И хотя все деформации будут постоянно происходить пропорционированно, и каждый кадр изменения фигуры, например, четырех точек, в движении называют гармоничным, это не всегда соответствует действительности. Гармоничное пропорционирование деформации элементов каждого кадра фигуры происходит только тогда, когда высота и ширина (для плоскости), и длина (для объема) исходной фигуры проектировались по соизмерительным инструментам, содержащим золотые числа. Все другие пропорции не приводят к получению гармоничного отношения. Поскольку объемное пропорционирование по золотым пропорциям еще не устоялось и не применяется в проективной и начертательной геометрии, разберем несколько примеров пропорционирования фигур на плоскости.

Основная задача статико-динамической геометрии – нахождение элементов фигур, пропорционированных в золотых числах, и обеспечение возможности перенесения этих пропорций на любой элемент внешней фигуры. Выше показаны два способа проведения гармонического пропорционирования как отрезка АВ, так и базисной прямой точками N и М: методом пирамиды Дезарга и методом параллельных Евклида. Оба способа дают аналогичные результаты и отличаются лишь трудоемкостью их исполнения. Оба способа начинаются с выбора отрезка АВ и деления его в произвольном отношении точкой N – следом поляры. И только две точки на этом отрезке могут обусловить появление золотых пропорций. Естественно, что в проектировании фигур или объектов эти точки могут проявить себя только при целенаправленном выборе. Не останавливаясь на описании использования золотых пропорций, приведем пример пропорционированого переноса в пространстве плоской фигуры.

Дата добавления: 2014-12-07