Преобразователи ПКН и ПНК

В САУ с ЦВМ, как правило, входят ПНК и ПКН. Процесс преобразования непрерывного сигнала в дискретный состоит из трёх этапов:

1) квантование по времени;

2) квантование по уровню;

3) к одирование.

Квантование по времени связано с последовательностью (очередностью) выполнения математических операций.

Квантование по уровню необходимо для представления информации в цифровом виде. Квантование производится следующим образом: весь диапазон изменения непрерывной величины x(t) разбивается на N равных частей.

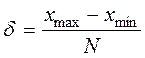
где d — шаг квантования по уровню (цена младшего разряда). В результате сигнал приобретает ступенчатый вид, показанный на рис. 2.2.1.

Рисунок 2.2.1.

Рассмотрим функциональную схему преобразователя напряжения в код.

Кодирование представляет собой преобразование входного сигнала в двоичный параллельный код УЦВМ. Это преобразование осуществляется с помощью триггеров, механическая модель которых показана на рис. 2.2.2а. Триггер представляет собой устройство с двумя устойчивыми положениями равновесия. Одному положению присваивается значение 0, другому – значение 1. Каждому разряду соответствует свой триггер. При перебрасывании триггера из положения «1» в «0» в старший разряд посылается сигнал на переключение соответствующего ему триггера и т.д. На рис. 2.2.2б представлена функциональная схема ПНК.

а)

б)

Рисунок 2.2.2. Функциональная схема преобразователя ПНК.

На рис. 2.2.2 u_x — непрерывный сигнал, который надо преобразовать в двоичный параллельный код,

& — элемент «И», который срабатывает только тогда, когда на все его входы подаются отличные от 0 сигналы,

ГПИ - генератор последовательности импульсов,

В ПНК составной частью входит ПКН,

– сигнал обратной связи.

u_э - эталонное напряжение,

a - количество разрядов,

u₁,u₂,…,u_a — сигналы соответствующих разрядов,

2⁰,2¹,…,2^a-1 — весовые коэффициенты разрядов.

Для многих цифровых систем шаг квантования сигнала по уровню, является настолько малым, что эффект квантования по уровню вызывает несущественное влияние и им часто пренебрегают, однако в высокоточных системах их приходится учитывать.

2.3 Понятие о решётчатых функциях и разностных уравнениях.

Дискретная САУ получает входную информацию и выдаёт выходную информацию в дискретные моменты времени. Поэтому при исследовании дискретных систем рассматривается их поведение только в дискретные моменты времени nT₀, где Т₀ такт счёта, n =0,1,2,… — номер такта счёта. Для этого вводится понятие решётчатых функций.

Решётчатой называют функцию, которая существует лишь в дискретные равноотстоящие друг от друга значения времени и в промежутках между этими значениями равна нулю. На рис. 2.3.1 сплошными вертикальными линиями показана решетчатая функция f[nT₀].

Рисунок 2.3.1.

Непрерывной функции (пунктирная кривая) соответствует одна и только одна решётчатая функция, а одной решётчатой функции соответствует бесконечное количество непрерывных функций.

Часто в цифровых САУ используется безразмерное время. Пусть безразмерное непрерывное время определено выражением

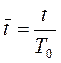, (2.3.1)

тогда безразмерное дискретное время будет

, n=0,1,2,… (2.3.2)

Непрерывные системы обычно описываются дифференциальными уравнениями. Дискретные системы описываются разностными уравнениями. Рассмотрим разностные уравнения и их соотношения с дифференциальными уравнениями. Для операции дифференцирования можно записать

,

т.е. операции дифференцирования с точностью до коэффициента 1/Т₀ соответствует операция вычитания (разность).

В безразмерном времени разности обозначают так:

– первая прямая разность,

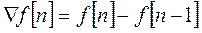– первая обратная разность, (2.3.3)

где 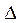- оператор «дельта», 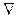- оператор «набла».

Аналогом второй производной по времени являются вторая прямая и обратная разности.

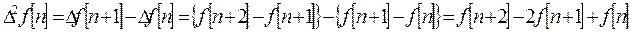
. (2.3.4)

Аналогично можно получить разности более высоких порядков.

Дискретным аналогом интеграла является полная сумма

. (2.3.5)

Выше была установлена связь между производной и конечными разностями и интегралом и суммой. Дифференциалы и интегралы используются для описания систем в непрерывном времени в виде дифференциальных и интегральных уравнений. Поведение дискретной системы в дискретные моменты времени описывается разностными уравнениями. Разностными уравнениями можно описать и непрерывную систему, но её поведение будет характеризоваться только в дискретные моменты времени. Рассмотрим связь между дифференциальными и разностными уравнениями на примере

.

С помощью полученных выше соотношений составляем разностное уравнение, используя обратные разности

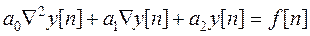
или

,

или

,

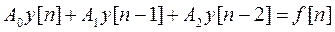где

, .

Если f[n]= 0, то разностное уравнение называется однородным, если f[n]¹ 0, то разностное уравнение называется неоднородным.

В общем случае разностное уравнение можно представить в виде

(2.3.6)

(6) — разностное уравнение к-го порядка. Для решения необходимо знать начальные условия, т.е. значения y(n) в предыдущие моменты времени y(0), y(1), y(k-1).

В дифференциальных уравнениях для сведения к алгебраическому уравнению используют оператор дифференцирования 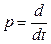. Для решения разностного уравнения путём сведения его к алгебраическому уравнению используют оператор сдвига z, так что

и т.д… (2.3.7)

С помощью оператора сдвига уравнение (6) перепишется в виде

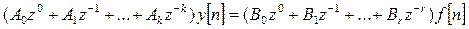, (2.3.8)

откуда формально можно записать

, (2.3.9)

где 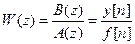─ передаточная функция дискретной системы. Если в W(z) знаменатель приравнять к нулю, то получится характеристическое уравнение, соответствующее разностному уравнению (6).

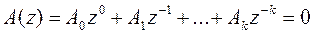(2.3.10)

Дата добавления: 2014-12-07