Частотные характеристики дискретных систем

Передаточные функции СРП (регулятора). Формула Тастина.

Передаточные функции замкнутых дискретных САУ.

Передаточная функция разомкнутой цепи

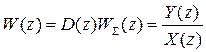(2.9.1)

Условием замыкания системы будет уравнение

(2.9.2)

Решая совместно уравнения (1) и (2), найдём

(2.9.3)

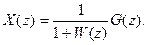(2.9.4)

Из (3) и (4) можно записать

(2.9.5)

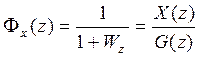, (2.9.6)

где – передаточная функция замкнутой САУ (главный оператор),

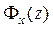– передаточная функция замкнутой САУ по ошибке.

Передаточная функция определяется выражением

.

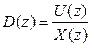Передаточная функция D(z) описывает алгоритм переработки входной последовательности чисел x[nT₀] в выходную u[nT₀] в соответствии с принятой программой вычислений. В общем виде закон управления имеет вид

.

В качестве примера рассмотрим типовые регуляторы: ПИ-, ПД-, ПИД- регуляторы, которые в непрерывном времени в общем виде выглядят так:

. (2.10.1)

Операции дифференцирования в непрерывном времени соответствует разность

Тогда передаточная функция дискретного дифференциатора

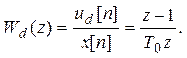(2.10.2)

Операции интегрирования

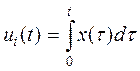
сопоставляется суммирование. По формуле трапеций получим соответствующее разностное уравнение

. (2.10.3)

Для предыдущего значения

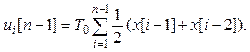(2.10.4)

Вычитая из (3) (4), получим

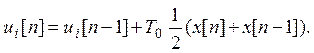(2.10.5)

В отличие от (3) выражение (5) является рекурентным. (Рекурентность – свойство последовательности, заключающееся в том, что любой ее член может быть вычислен по значениям предыдущего или нескольких предыдущих членов).

В операторном виде выражение (5) будет выглядеть так:

. (2.10.6)

Дискретная передаточная функция интегратора в соответствии с (6) выглядит следующим образом:

. (2.10.7)

Формула (7) называется формулой Тастина.

Дискретный позиционный сигнал с передаточной функцией определяются выражениями

(2.10.8)

Помимо дискретной передаточной функции дифференциатора (2), полученной с применением конечных разностей, из формулы Тастина (7) можно получить более точную формулу дифференциатора

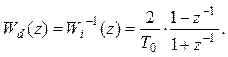(2.10.9)

ПИД—регулятор в непрерывном времени с его передаточной функцией описываются выражениями

.

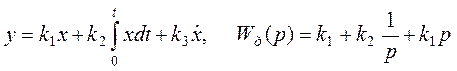ПИД—регулятор в дискретном времени имеет передаточную функцию, записанную с помощью выражений (8), (7), (9), в виде

. (2.10.10)

Дискретное уравнение ПИД—регулятора можно получить из второго равенства в (10), а именно

.

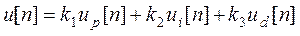С частотными характеристиками дискретных систем сталкиваются при рассмотрении установившейся реакции дискретной цепи на входной сигнал в виде гармонической решётчатой функции, а также при исследовании устойчивости дискретных систем. Гармоническая решётчатая функция имеет вид

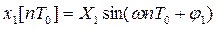(2.11.1)

На рис. 1 представлен график функции (1)

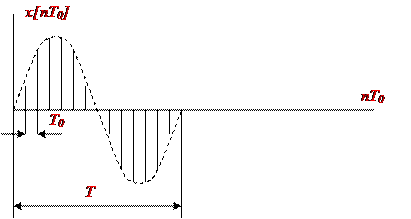
Рисунок 2.11.1. Гармоническая решеточная функция

На рис. 1 приняты следующие обозначения: Т – период гармонической функции; Т₀ – такт счёта. Соответствующие частоты квантования и гармонической функции определяются выражениями

. (2.11.2)

В непрерывных системах для исследования их частотных свойств теоретически рассматривают диапазон частот от нуля до бесконечности, а на практике в рабочей полосе частот, которая всё равно является широкой. Определим, в каком диапазоне частот надо исследовать частотные характеристики дискретных систем. Для этого в функции (1) дадим приращение частоты величиной kw₀, где k – целое число.

(2.11.3)

Сравнивая выражения (1) и (3), приходим к выводу, что при k =1,2,… функции х₁, и х₂ совпадают. Отсюда можно заключить, что для исследования частотных свойств дискретных систем достаточно рассмотреть диапазон частот от нуля до w₀.

В непрерывных системах для получения частотных характеристик надо в передаточную функцию сделать подстановку p=jw. В дискретных системах для получения частотных характеристик надо в передаточную функцию сделать подстановку

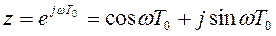. (2.11.4)

В результате получим

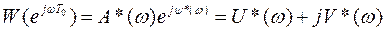, (2.11.5)

где A*(w); y*(w) – АЧХ и ФЧХ дискретной системы;

U*(w); V*(w) – действительная и мнимая части АФЧХ.

На основании (3), (5) можно заключить, что все частотные характеристики достаточно рассмотреть в диапазоне частот от нуля до w₀. Построение АФЧХ, АЧХ, и ФЧХ производится, в функции частоты . Построение ЛАЧХ и ЛФЧХ производится, как правило, в функции псевдочастот и l, т.к. при этом сохраняются асимптотические свойства ЛАЧХ. Для перехода к псевдочастотам применяется 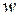-преобразование по зависимостям

. (2.11.6)

(См. аппроксимацию Тастина (2.10.9)). Переходя к частотной функции заменой (4), получим

, (2.11.7)

где - относительная псевдочастота.

Для получения абсолютной псевдочастоты используют зависимость

.

При достаточно малом 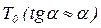можно записать

,

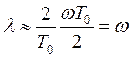т.е. при достаточно малом Т₀ абсолютная псевдочастота совпадает с несущей частотой w (с частотой гармонического сигнала), т.е. при достаточно матом Т₀ частотные характеристики дискретных и непрерывных систем близки.

Дата добавления: 2014-12-07