Плоская система сходящихся сил

Статика

Тема 2.9. Понятие о действии динамических и повторно-переменных нагрузок

Обычно расчеты на усталость проводятся не как проектные (определение разме­ров сечения детали), а как проверочные. Объясняется это тем, что допускаемое на­пряжение не может быть установлено заранее достаточно точно, так как оно зависит не только от материала детали, но и от ряда ее конструктивных особенностей (разме­ров, качества обработки поверхности, наличия концентратов напряжения).

Вопросы для самоконтроля

1. Как называется механическая характеристика материала, определяющая его сопротивление переменным напряжениям?

2. Что такое концентрация напряжения? Приведите примеры деталей, имеющих концентраторы напряжений?

3. Какие факторы влияют на снижение предела выносливости?

Раздел 1. Теоретическая механика

Во всех задачах рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Для задач этого типа универсальным является аналитический метод решения.

Последовательность решения задачи:

1. выбрать тело (точку), равновесие которого следует рассматривать;

2. освободить тело (шарнир В) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принято считать предположительно стержни растянутыми;

3. выбрать систему координат, совместив ее начало с точкой В, и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ΣXi=0; ΣYi =0;

4. определить реакции стержней из решения указанной системы уравнений;

5. проверить правильность полученных результатов по уравнению, которое не использовалось при решении задачи, либо решить задачу графически.

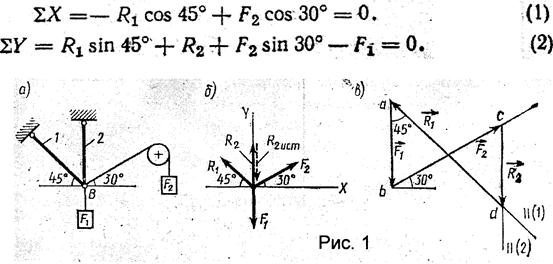
Пример 1. Определить реакции стержней, удерживающих грузы F₁=70 кН и F₂=100 кН (рис. 1, а). Массой стержней пренебречь.

1. Рассматриваем равновесие шарнира В (рис. 1, а).

2. Освобождаем шарнир 3 от связей и изображаем действующие
на него активные силы и реакции связей (рис. 1, а).

3. Выбираем систему координат и составляем уравнения равновесия
для системы сил, действующих на шарнир В.

4. Определяем реакции стержней Ri и R2, решая уравнения (1), (2).

Из уравнения (I)

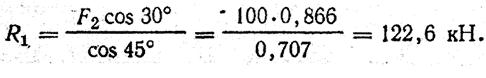
Подставляем найденное значение R₁ в уравнение (2) и получаем

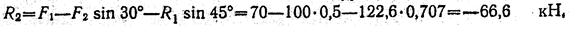
Знак минус перед значением R₂ указывает на то, что первоначально выбранное направление реакции неверное — следует направить реакцию R₂ в противоположную сторону, т. е. к шарниру В (на рис. 1, б истинное направление реакции R₂ показано штриховым вектором).

5. Проверяем правильность полученных результатов, решая задачу графически (рис. 1, в). Полученная система сил (рис. 1, б) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.

Строим силовой многоугольник в следующем порядке (рис. 1, в): в выбранном масштабе (например, µ_сил=2 кН/мм) откладываем заданную силу 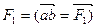, затем из точки b под углом 30° к горизонту откладываем силу 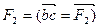, далее из точек а и с проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник abcd, в котором сторона 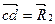? а сторона 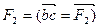. Измерив длины этих сторон (в мм) и умножив на масштаб построения µ_сил, получаем значения реакций стержней: R₂ = cd· µ_сил = 33·2=66 и R₁ =d·a· µ_сил= 61·2=122 кН.

Графическое решение подтверждает правильность первого решения.

Дата добавления: 2014-12-07