Работа и мощность

Задачи 51-—80 на работу и мощность либо при поступательном либо при вращательном движении. Задачи следует решать, изучив темы 1.14 и 1.15, а также повторив материал о трении скольжения и качения. Решая данные задачи, необходимо внимательно следить за тем, чтобы числовые значения величин были выражены в единицах СИ.

Задача 51. Вертолет, масса которого с грузом 6 т, за 2,5 мин набрал высоту 2250 м Определить мощность двигателя вертолета.

Задача 52. Автомобиль весит 9000 Н. Найти силу тяги и мощность, развиваемую двигателем автомобиля, если его скорость равна 36 км/ч при движении в гору с уклоном в 12°. Коэффициент трения 0,1.

Задача 53. Поезд идет со скоростью 36 км/ч. Мощность тепловоза 300 кВт, коэффициент трения 0,004. Определить вес всего состава.

Задача 54. Для подъема 5000 м3 воды на высоту 3 м поставлен насос с двигателем мощностью 2 кВт. Сколько времени потребуется для перекачки воды, если КПД насоса равен 0,8?

Задача 55. Динамометр, установленный между теплоходом и баржей, показывает силу тяги 30 кН, скорость буксировки 18 км/ч, мощность двигателя 550 кВт. Определить силу сопротивления воды корпусу буксира, если КПД силовой установки и винта равен 0,4.

Задача 56. Транспортер поднимает груз массой m=200 кг на автомашину за время t=1 с. Длина ленты транспортера L=3 м, а угол наклона а=30°. Коэффициент полезного действия транспортера η =85 %. Определить мощность, развиваемую его электродвигателем.

Задача 57. Точильный камень диаметром 0,5 м делает 120 об/мин. Обрабатываемая деталь прижимается к камню с силой F=10 H. Какая мощность затрачивается на шлифовку, если коэффициент трения камня о деталь f =0,2?

Задача 58. Определить работу силы трения скольжения при торможении вращающегося диска диаметром d=200 мм, сделавшего до остановки два оборота, если тормозная колодка прижимается к диску с силой F=400 H. Коэффициент трения скольжения тормозной колодки по диску равен 0,35.

Задача 59. Колесо зубчатой передачи, передающей мощность Р=12 кВт, вращается с угловой скоростью ю=20 рад/с. Определить окружную силу, действующую на зуб колеса, если диаметр колеса d=360 мм.

Задача 60. Маховик вращается вместе с горизонтальным валом цапфы (участки опирающиеся на подшипники) которого имеют диаметр d=100 мм. Нагрузка на каждый из двух подшипников F=4 кН. Приведенный коэффициент трения скольжения в подшипниках f=0,05. Определить работу, затрачиваемую на преодоление трения за два оборота маховика.

РАЗДЕЛ 2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Первая задача (задачи 61—70).

Требует от учащегося умения строить эпюры продольных сил, нор­мальных напряжений и определять удлинения или укорочения бруса.

При работе бруса на растяжение и сжатие в его поперечных сечениях возникает продольная сила N. Продольная сила в произвольном попереч­ном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсеченную часть.

Для расчёта на прочность и определения перемещений необходимо знать закон изменения продольных сил по его длине. Правило знаков: при растяжении продольная сила положительна, при сжатии — отрицательна. Условие прочности при растяжении и сжатии имеет вид где σ, N - соответственно нормальное напряжение и продольная сила в опасном сечении (т. е. в сечении, где возникают наибольшие напряжения); А — площадь поперечного сечения; [σ] — допускаемое напряжение. Исходя из усло­вия прочности, можно решать три вида задач: 1) проверка прочности; 2) под­бор сечения А ≥ N/[σ]; 3) определение допускаемой нагрузки N ≤[σ]А.

Последовательность решения задачи:

1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и места изменения размеров поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам

3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Пример 4. Для данного ступенчатого бруса (рис. 8, а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если:

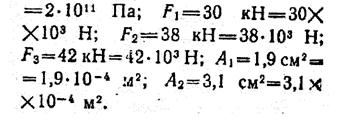
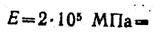
Решение:

1. Разбиваем брус на участки, как показано на рис. 8, а. 2.

2. Определяем ординаты эпюры N на участках бруса:

Строим эпюру продольных сил (рис. 8, 6).

3. Вычисляем ординаты эпюры нормальных напряжений:

Строим эпюру нормальных напряжений (рис. 8, в).

4. Определяем перемещение свободного конца:

Брус удлиняется на 0,23 мм.

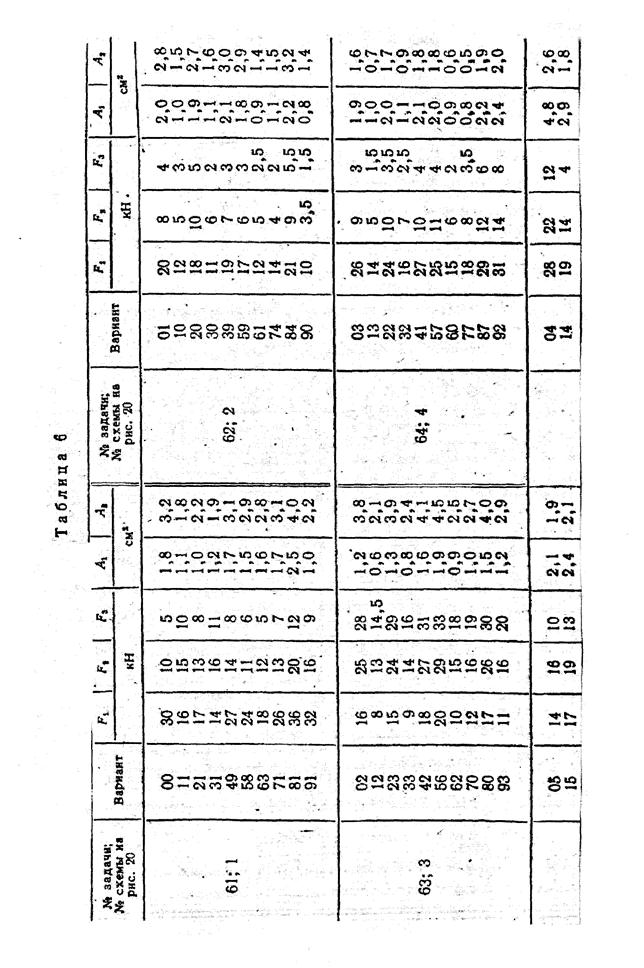
Задачи 61—70. Двухступенчатый стальной брус, длины ступеней которого указаны на рис. 20 (схемы 1—10), нагружен силами F₁, F₂ и F₃. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆ l свободного конца бруса, приняв Е=2·10⁵ МПа. Числовые значения F₁, F₂, F₃, а также площади поперечных сечений ступеней A₁ и А₂ для своего варианта взять из табл. 6.

Рис. 20

Вторая задача (задачи 71—80).

В задачах 71—80 рассматриваются статически неопределимые сис­темы с числом неизвестных реакций, связей, на единицу превышающим числом уравнений статики (уравнений равновесия), которые можно соста­вить для этой системы (задачи — один раз статически неопределимые).

Последовательность решения задачи:

1. Брус, равновесие которого рассматривается, освободить от связей и заменить действие связей их реакциями; определить степень статической неопределимости как разность между количеством неизвестных и числом уравнений статики.

2. Составить уравнение равновесия; в него войдут обе неизвестные реакции связей, без которых невозможно определить продольные силы, возникающие в брусе или стержне.

3. Рассмотреть картину перемещений системы и на основе ее рассмотрения с геометрической точки зрения составить уравнение перемещений, в которое войдут те же неизвестные реакции, что и в уравнение статики. Причем, перемещения (удлинения или укорочения) участков бруса определяем по формуле Гука λ=∆ l =N/EA.

4. Уравнение статики и уравнение перемещений решить совместно и определить искомые реакции связей.

5. Определить внутренние силовые факторы (продольные силы) в частях деформируемого бруса или в стержнях или же (если в задаче требуется определить допускаемую нагрузку) выразить продольные силы через искомую нагрузку.

6. Произвести заданный в условии задачи расчет. Рассмотрение ряда конкретных примеров позволит получить представление о методике решения статически неопределимых за­дач.

Пример 5. Для заданного двухступенчатого бруса (рис. 9) рас­крыть статическую неопределимость, построить эпюры N и а по длине бруса, проверить прочность в опасном сечении и вычислить процент перегрузки (недогрузки) бруса, если

Решение.

1. Задача один раз статически неопределима, так как уравнение статики одно (ΣZ=0), а неизвестных реакций две.(рис. 9, а).

2. Составляем уравнение равновесия

ΣZ = 0; -R_B + F-RD-=0 (1)

3. Составляем уравнение перемещений. Под действием внешних сил F, R_D, R_B длина бруса вследствие жесткого защемления его концов должна при деформации оставаться неизменной; это условие и используем для составления уравнения перемещений.

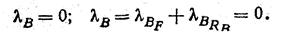Отбросим мысленно нижнюю заделку, заменив ее реакцией R_B (рис. 9,б), получим брус, эквивалентный данному, для которого пере­мещение λ в сечения В равно нулю:

(2)

Для составления уравнения (2) применён принцип независимости действия сил, т.е. перемещение от совместного действия всех сил равно алгебраической сумме перемещений от действия каждой силы в отдельности. λ_BF= F-1,5 l /(E-1,2A)- удлинение участка DC (рис. 9, б) от силы F.

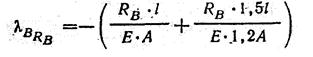- сумма укорочении участков DC и СВ (рис. 9, б) от действия силы Rb.

4. Решая совместно уравнения статики (1) и уравнение перемещений (2), определяем неизвестные реакции R_D и R_B.

Из (2):

5. Определяем внутренние силовые факторы по участкам бруса и строим эпюры продольных сил и нормальных напряжений по длине бру­са/

Статическая неопределимость раскрыта — имеем статически опреде­лимый брус, заделанный одним концом, нагруженный известными силами F и R_B (см. рис. 9, б). Эпюры продольных сил и нормальных напряжений строим, как для статически определимого бруса (рис. 9, б, г).

6. Наибольшие по абсолютному значению напряжения возникают в поперечных сечениях участка ВС — это опасные сечения.

Определяем процент перегрузки:

Пример 6. Для бруса (рис. 10, а) раскрыть статическую неопределимость и определить из условия прочности допускаемое значение силы F, если

E = 2·10⁵ МПа; [σ]=160 МПа.

При требуемом значении силы F построить эпюру продольных сил и нор­мальных напряжений.

Решение. Принцип решения данной задачи такой же, как в примере 5.

1. Задача один раз статически неопределима, так как уравнение ста­тики можно составить лишь одно ΣZ=0, а неизвестных два - Ro и Rb (рис. 10, а).

2. Уравнение статики: ΣZ=0; -Ro-R_B+2F+3F=O

3. Уравнение перемещений (рис. 10, б):

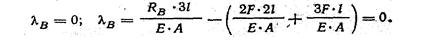
4. Из уравнения перемещений и уравнения статики получаем:

5. Определяем продольные силы по участкам бруса, выражая их значения через F:

6. Так как площадь поперечных сечений бруса постоянна по всей его длине, то опасными будут сечения на участках бруса с наибольшим значением продольной силы. Следовательно

Тогда, исходя из условия прочности [N]=8/3F = [σ]A, получаем

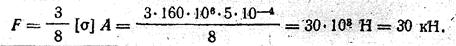
Строим эпюру продольных сил N, принимая F=30 кН (рис. 10, в), и эпюру нормальных напряжений а (рис. 10, г).

Пример 7. Определить площадь поперечных сечений стальных стержней, удерживающих абсолютно жесткую балку (рис. 11, а), если [σ]=160 МПа, l =а=1м; F=100 кН. Площадь А поперечных сечений стерж­ней одинакова.

Решение.

1. Задача один раз статически неопределима, так как число неизвестных сил четыре: R_oz, R_oy, N₁, N₂ (рис. 11, б), а уравнений равновесия статики три.

2. Уравнение статики.

3. Картина перемещений изображена на рис. 11, в, из которой нахо­дится геометрическая зависимость между перемещениями стержней ∆ l ₁ и ∆ l 2 и длинами ОВ и ОС. Из подобия ∆OBB₁ и ∆OCC₁ (рис. 11, в) составля­ем уравнение перемещений:

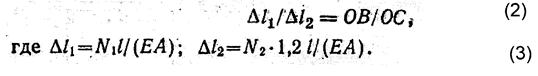
4.:Из уравнения перемещений (2) имеем:

Используя зависимость (3), решаем уравнение (1):

5. Продольные силы в стержнях 1 и 2 численно равны силам N₁ и N₂

6. Определяем площадь поперечных сечений из условия прочности:

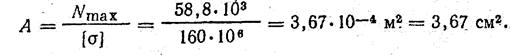
Пример 8. Конструкция, состоящая из трех стальных стержней, со­единенных шарнирно (рис. 12, а), нагружена силой F. Все стержни имеют одну и ту же площадь поперечного сечения А. Определить силы в стерж­нях и перемещение шарнира О.

Решение.

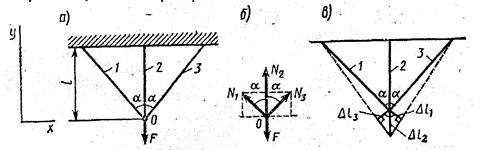
1. В данном примере в шарнире О приложена система сходящихся сил, для которой можно составить лишь два уравнения статики ΣХ=0, ΣY=0; неизвестных сил три (рис. 12, б). Следовательно, данная задача один раз статически неопределима.

2. Из условия равновесия узла О (рис. 12, в) составляем уравнения статики (1) и (2):

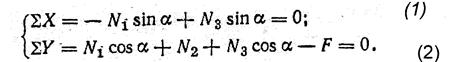
Из (1) получаем N₃=N₁. Подставляя вместо N₃ во второе уравнение значение N₁ получаем

3. Очевидно, шарнир О переместится по вертикали вниз. Из схемы перемещений (рис. 12, в) заключаем, что уравнение перемещений имеет следующий вид:

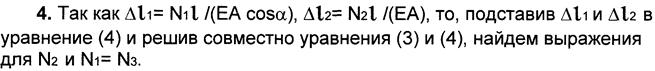
5. Определив продольные силы N₁, N₂, N₃; получим их выражение через внешнюю нагрузку F.

6. Перемещение шарнира О равно

Подставив в выражение (5) найденное значение N₂ и заданное значе­ние угла α, определим перемещение шарнира О.

Задачи 71 — 73. Для данного двухступенчатого бруса, размеры ко­торого показаны на рис. 21 (схемы 1, 2, 3), раскрыть статическую неопре­делимость, построить эпюры продольных сил и нормальных напряжений по длине бруса и определить, на сколько процентов перегружен или не­догружен брус в опасном сечении. Принять Е=2·10⁵ МПа; [σ]=160 МПа.

Задачи 74 — 76. Определить из условия прочности допускаемое значение силы для заданного стального бруса постоянного поперечного сечения (рис. 21, схемы 4, 5, 6). Определив допускаемое значение силы F, построить по длине бруса эпюры продольных сил и нормальных напряже­ний.. Принять Е=2·10⁵ МПа; [σ]=160 МПа.

Задачи 77 — 78. Из условия прочности определить размер попе­речного сечения стальных стержней (рис. 21, схемы 7, 8), удерживающих в равновесии абсолютно жесткий брус, шарнирно закрепленный одним кон­цом, если [σ]=160 МПа, Е=2·10⁵ МПа. Определив площадь А, найти на­пряжения в поперечных сечениях стержней.

Задачи 79, 80. Конструкция, состоящая из трех стальных стержней, соединенных шарнирно, нагружена силой F (рис. 21, схема 9). Все стержни имеют одну и ту же площадь поперечного сечения А. Принять [σ] = 160 МПа. В задаче 79 определить силы в стержнях и найти площадь попереч­ного сечения А из условия прочности. В задаче 80 определить силы в стержнях и перемещение шарнира О. Для задачи 79: l =1 м; α=30°; F=30 кН. Для задачи 80: l =1,5 м; α=35°; F=40 кН.

Третья задача (задачи 81—90). К решению этой задачи следует приступить после изучения темы «Кручение».

Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — крутящий момент Мк (или Mz).

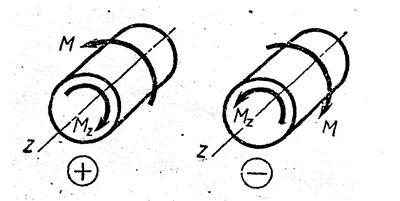Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на отсеченную часть: Mк=ΣM₁ (имеется в виду, что плоскости действия всех внешних скручивающих моментов M₁ перпендикулярны продольной оси бруса).

Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке. Соответствующий внешний момент направлен против часовой стрелки (рис. 13).

В третьей задаче необходимо выполнить проектный расчет вала круг­лого поперечного сечения из условий прочности и из условий жесткости; из двух полученных значений диаметров следует выбрать наибольшее значение.

Последовательность решения задачи:

1. Определить внешние скручивающие моменты по формуле М=Р/ω, где Р — мощность, ω — угловая скорость.

2. Определить уравновешивающий момент, используя уравнение равновесия ΣМ=0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.

3. Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.

4. Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала для круглого сечения из условий прочности и жесткости.

Из двух полученных диаметров вала выбрать наибольший.

Пример 9. Для стального вала (рис. 14) круглого поперечного сече­ния постоянного по длине (рис. 14, а) требуется:

1. Определить значения моментов М₂ и М₃, соответствующие передаваемым мощностям Р₂ и Р₃, а также уравновешивающий момент M₁.

2. Построить эпюру крутящих моментов.

3. Определить требуемый диаметр вала из расчетов на прочность и жесткость, если

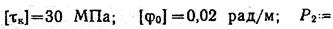
Окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа.

Решение:

1. Определяем величины внешних скручивающих моментов М₂ и М₃:

2. Определяем уравновешивающий момент M₁:

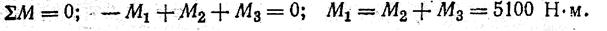
3. Строим эпюру M_z (рис. 14, б).

4. Определяем диаметр вала из условий прочности и жесткости. M_zmax=5100 НМ (рис. 14, б).

Требуемый размер сечения получился больше из расчета на проч­ность, поэтому его принимаем как окончательный: d=95 мм.

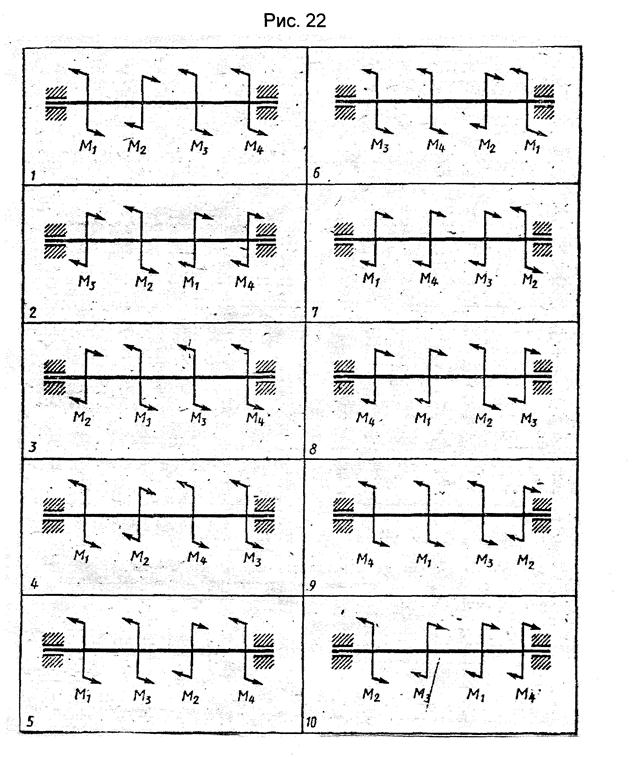
Задачи 81—90. Для стального вала постоянного поперечного сече­ния (рис. 22, схемы 1—10):

1. определить значения моментов M₁ М₂, М₃, М₄;

2. построить эпюру крутящих моментов;

3. определить диаметр вала из расчетов на прочность и жесткость.

Принять [τ_к] =30 МПа; [φо] =0,02 рад/м. Данные своего варианта взять из табл. 7. Окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего большего четного или оканчивающегося на пять числа.

Четвертая задача (задачи 91—100). К решению этой задачи следует приступить после изучения темы «Изгиб». Изгиб — это такой вид деформации бруса, при котором в его поперечных сечениях возникают из­гибающие моменты. В большинстве случаев одновременно с изгибающи­ми моментами возникают и поперечные силы; такой изгиб называют попе­речным; если поперечные силы не возникают, изгиб называют чистым. Из­гибающий момент Ми в произвольном поперечном сечении бруса числен­но равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно центра тяжести сечения: Ми=ΣМ. Попе­речная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на отсеченную часть: Q=ΣF. Причем все внешние силы и моменты действуют в главной про­дольной плоскости бруса и расположены перпендикулярно продольной оси бруса.

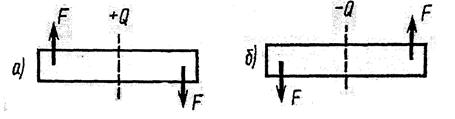
Правило знаков для поперечной силы: силам, поворачивающим отсе­ченную часть балки относительно рассматриваемого сечения по ходу ча­совой стрелки, приписывается знак плюс (рис. 15, а), а силам, поворачи­вающим отсеченную часть балки относительно рассматриваемого сечения против хода часовой стрелки, приписывается знак минус (рис. 15, б).

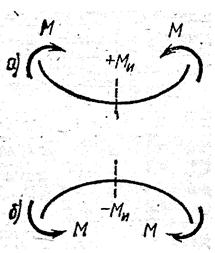
Правило знаков для изгибающих моментов: внешним моментам, из­гибающим мысленно закрепленную в рассматриваемом сечении отсечен­ную часть бруса выпуклостью вниз, приписывается знак плюс (рис. 16, а), а моментам, изгибающим отсеченную часть бруса выпуклостью вверх — знак минус (рис. 16, б).

Между выражениями изгибающего момента М_х, поперечной силы Q_y и интенсивностью распределенной нагрузки q существуют дифференциальные зависимости:

Между выражениями изгибающего момента Мх, поперечной силы Qy и интенсивностью распределенной нагрузки q существуют дифференциальные зависимости:

На основе метода сечений и дифференциальных зависимостей устанав­ливается взаимосвязь эпюр М_х и Q_y между собой и с внешней нагрузкой, поэтому достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями.

Характерными являются сечения балки, где приложены; сосредоточенные силы и моменты (включая опорные се­чения), а также сечения, ограничивающие участки с равномерно распре­деленной нагрузкой.

Приведём некоторые правила построения эпюр.

Для эпюры поперечных сил:

1. На участке, нагружённом равномерно распределенной нагрузкой, эпюра изображается прямой, наклоненной к оси балки.

2. На участке, свободном от распределенной нагрузки, эпюра изображается прямой, параллельной оси балки.

3. В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет своего значения.

4. В сечении, где приложена сосредоточенная сила, эпюра поперечных сил меняется скачкообразно на значение, равное приложенной силе.

5. В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю.

Дата добавления: 2014-12-07