Соотношения неопределенностей

1. Отсутствие траектории у микрочастицы указывает на то, что описывать ее состояние столь же подробно как для материальной точки нельзя.

Действительно, задание координат и импульса материальной точки в какой то момент времени позволяет рассчитать ее состояние в любой другой момент и определить ее траекторию, пользуясь формулами

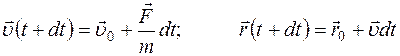
Отсутствие траектории у микрочастицы свидетельствует о том, что она не имеет одновременно точных значений координат и импульса (скорости). В противном случае мы могли бы точно предсказать ее положение в следующий момент времени, т.е. определить траекторию.

Отсутствие у микрочастицы одновременно точных значений координат и импульса говорит о том, что они обладают неопределенностью. Это утверждение составляет содержание принципа неопределенности Гейзенберга, сформулированного в 1927 году.

2. Описание состояния в квантовой механике с той же полнотой, что и в классической невозможно. Поэтому квантовая механика дает только вероятностные предсказания о поведении микрочастицы. Пользуясь волновой функцией Y(z) можно определить распределение плотности вероятности по координате z и с ее помощью определить среднеквадратичное отклонение, которое принимают за квантовую неопределенность в значении координаты

,

где

.

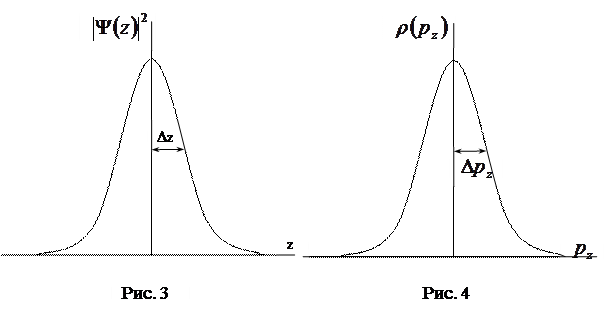
На рис. 3 показан один из вариантов распределения плотности вероятности по координате z.

3. Зная волновую функцию 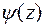для конкретной ситуации, можно определить распределение плотности вероятности 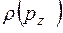по проекциям импульса (рис. 4) и ввести квантовую неопределенность импульса

,

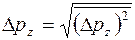где

.

4. Квантовые неопределенности сопряженных координаты и проекции импульса не могут быть сколь угодно малыми, и связаны друг с другом соотношением неопределенности Гейзенберга

, , .

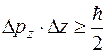Эти неравенства показывают, что уменьшение неопределенности координаты приводит к возрастанию неопределенности сопряженной проекции импульса и наоборот.

Кроме этих неравенств есть еще неравенство, связывающее энергию состояния и время его существования

.

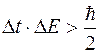Это неравенство означает, что чем короче время существования какого-либо состояния или время, отведенное для его наблюдения, тем с меньшей определенностью можно говорить об энергии этого состояния.

Дата добавления: 2014-11-29