Минимальная энергия и размеры атома

Пределы применимости классической механики

1. Соотношения неопределенностей Гейзенберга для координат и импульсов отражают тот факт, что в природе объективно не существует состояний микрочастиц с точно определенными значениями координат и импульсов.

В частном случае неопределенности импульса может и не быть (). Так будет, например, в случае плоской монохроматической волны де Бройля. Но в этом случае, согласно неравенствам Гейзенберга неопределенности координат обращаются в бесконечность , и о месте, где локализована микрочастица, ничего сказать нельзя. Она может быть с одинаковой вероятностью обнаружена в любой точке пространства. (Плоская волна имеет бесконечную протяженность, как по фронту, так и вдоль направления распространения).

При локализации микрочастицы в какой-то точке пространства неопределенности координат исчезают, а неопределенности импульсов возрастают до бесконечности, т.е. все значения импульса становятся равновероятными.

Соотношения неопределенностей определяют принципиальный предел неточности координат и сопряженных им проекций импульса, с которыми состояние частицы можно описывать классически и рассчитывать их траектории.

2. Обратимся к числовым оценкам, вытекающим из принципа неопределенности Гейзенберга. Будем считать его универсальным законом природы и рассмотрим, в каких случаях квантовые неопределенности в координатах и импульсах можно не учитывать.

Рассмотрим движение макроскопического тела с массой . Пусть неопределенность в определении ее положения Dz составляет , тогда неопределенность импульса

.

Отсюда неопределенность в возможных значениях скорости

.

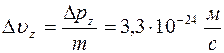Данные неопределенности настолько малы, что всегда заведомо меньше погрешности измерения. В этом случае мы можем при движении частицы не учитывать ее волновых свойств и считать ее классической.

Отступления от классического движения из-за принципа неопределенности лежат далеко за пределами возможностей эксперимента.

Рассмотрим теперь движение электрона в электронно-лучевой трубке. Скорость электронов по порядку величины составляет u_z = 10⁷м/с.

Если считать неопределенность значений скорости лежащей в пределах 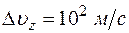, что составляет 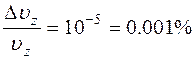, то неопределенность в координате 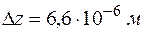. В этом случае также погрешности измерения скорости и координат превышают квантовые неопределенности и движение электрона можно считать классическим.

Совсем иначе обстоит дело с движением электрона в атоме. Возьмем атом водорода и первую боровскую орбиту. Правило квантования орбит по Бору

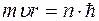
означает, что на круговой орбите укладывается целое количество длин волн де Бройля

и

.

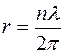Теперь если мы зададимся столь большой неопределенностью в положении орбиты, что , то

.

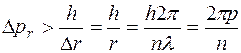Для первой боровской орбиты неопределенность в импульсе превысит величину самого импульса.

В этом случае представление о движении электрона по классическим орбитам теряет смысл. Неопределенности в координатах и импульсе столь велики, что движение является безтраекторным. В лучшем случае, понятием траектории можно пользоваться для высоких энергетических состояний (большие n).

Принцип неопределенности является одним из основных законов квантовой физики. Из принципа неопределенности вытекает ряд важных следствий. В частности состояние покоя для микрочастицы, движущейся в ограниченной области пространства невозможно, так как если неопределенность в координате положить равной размерам области движения, то неопределенность в импульсе будет конечной величиной. Это значит, импульс микрочастицы не может быть точно равен нулю.

Деление энергии на кинетическую и потенциальную теряет смысл, поскольку нет определенных значений скорости и расстояния r.

Принцип неопределенности позволяет объяснить тот факт, что электрон не падает на ядро атома, а также оценить размеры атома водорода.

Точное положение электрона в атоме запрещено принципом неопределенности: был бы бесконечно большой разброс в его импульсе. Поэтому для оценки наименьшей энергии 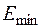электрона в кулоновском поле ядра можно положить разброс расстояний электрона от ядра и . Тогда из соотношения можно положить , и энергия может быть записана в виде

.

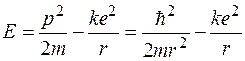Значение 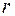, при котором 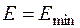, можно наитии из равенства нулю ее производной

.

Отсюда следует, что

.

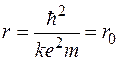Полученный результат совпадает с радиусом первой боровской орбиты в атоме водорода.

Для минимальной энергии получаем

,

что так же совпадает с энергией основного состояния атома водорода.

Совпадение наших грубых оценок с точными значениями r и E следует считать случайным. Важно лишь то, что получен верный порядок этих величин и что, основываясь на волновых представлениях, можно понять, почему электрон в атоме не падает на ядро. Размер атома является результатом компромисса двух слагаемых энергии, имеющих противоположные знаки. Уменьшение неопределенности в координате (уменьшение потенциальной энергии) приводит к увеличению неопределенности импульса (кинетической энергии).

Дата добавления: 2014-11-29